Campo y potencial eléctrico

Envia tus archivos, resúmenes, monografías, etc.

Preliminar. Ley de Coulomb. Principio de superposición. Campo eléctrico. Ley de Gauss. Potencial y energía eléctrica. Algunos casos particulares de potencial eléctrico. Carga puntual Campo eléctrico constante. Condensadores. Asociación de condensadores. Serie. Paralelo.

Agregado: 22 de JULIO de 2003 (Por Michel Mosse) | Palabras: 925 | Votar | Sin Votos | Sin comentarios | Agregar Comentario
Categoría: Apuntes y Monografías > Física >
Material educativo de Alipso relacionado con Campo potencial eléctrico

Concepto de dipolo eléctrico: aproximación microscópica a los medios materiales.: Campo local. Campo de la zona lejana. Campo de la zona próxima.

Biografia y vida de Francesco Camporesi: Breve Biografia de Francesco Camporesi

Energía potencial.: Energía potencial, Energía potencial de una bola, Energía cinética, Principio de conservación de la energía mecánica, Procedimientos.

Enlaces externos relacionados con Campo potencial eléctrico

Campo y potencial eléctrico

Preliminar

Las leyes de este tema y las formas de resolución de problemas son muy similares en forma y contenidos a las del tema anterior. Por esta razón se verán un poco más escuetamente sus leyes. De todas formas hay que tener en cuenta que esta analogía se produce entre dos magnitudes tan diferentes como la atracción gravitatoria y la eléctrica, cuya diferencia en órdenes de magnitud es del orden de .

Ley de Coulomb

Dos cargas eléctricas puntuales se atraen (o repelen) entre sí con una fuerza dada por

$\begin{displaymath} \vec{F} = \frac{1}{4\pi\epsilon_0}\frac{qQ}{r^2}\hat{r} \end{displaymath}$

(12.1)

Q y q son los valores de las cargas involucradas, que deberán llevar su correspondiente signo, $\epsilon_0$ se denomina permitividad del vacío. A veces al valor $\frac{1}{4\pi\epsilon_0}$ se le denota con la letra y su valor aproximado es de $9.00\cdot 10^9 Nm^2/C^2$ .

Principio de superposición

La fuerza que ejercen un sistema de cargas sobre otra es igual a la suma (vectorial) de las fuerzas de cada una de las cargas del sistema sobre la otra. Quiere decir esto que dado un sistema de cargas puntuales de posiciones $\vec{r}_i$ y cargas , la fuerza que ejercen sobre otra carga situada en $\vec{r}$ será

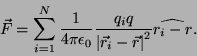
$\begin{displaymath}\vec{F} = \sum^N_{i=1} \frac{1}{4\pi\epsilon_0} \frac{q_i q}{ \left\vert \vec{r}_i - \vec{r} \right\vert^2}\widehat{r_i - r}.\end{displaymath}$

Campo eléctrico

Es la fuerza por unidad de carga que experimentará una carga en cierta posición del espacio. Obedece a la fórmula

$\begin{displaymath}\vec{E}=\frac{\vec{F}}{q}.\end{displaymath}$

Debido también al principio de superposición, la expresión del campo eléctrico en una posición $\vec{r}$ del espacio creado por un sistema de cargas de valor $q_i,\ i=1,\ldots N$ y posición $\vec{r}_i$ será

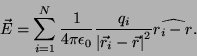
$\begin{displaymath}\vec{E} = \sum^N_{i=1} \frac{1}{4\pi\epsilon_0} \frac{q_i}{ \left\vert \vec{r}_i - \vec{r} \right\vert^2}\widehat{r_i - r}.\end{displaymath}$

En el caso de tener un sistema continuo esta fórmula anterior quedará transformada en

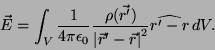
$\begin{displaymath}\vec{E} = \int_V \frac{1}{4\pi\epsilon_0} \frac{\rho(\vec{r'}... ...eft\vert \vec{r}' - \vec{r} \right\vert^2}\widehat{r' - r}\,dV.\end{displaymath}$

$\triangleright$ La fuerza y el campo eléctrico son magnitudes vectoriales que cumplen el principio de superposición. Por tanto se podrán sumar como vectores.

Ley de Gauss

Recordando que el flujo es la cantidad de campo vectorial que pasa por unidad de superficie, tendremos que, para el campo eléctrico $\vec{E}$ el flujo será

$\begin{displaymath}\phi_E = \int_S \vec{E}\cdot d\vec{S}.\end{displaymath}$

Siguiendo un razonamiento similar al que se puede realizar para el caso gravitatorio, la ley de Gauss nos dice que

$\begin{displaymath}\phi_E=4\pi KQ = \frac{Q}{\epsilon_0}.\end{displaymath}$

$\diamond$ En este caso, como las cargas pueden ser tanto positivas como negativas, puede resultar que, pese a que existan cargas en el interior de la superficie su carga neta sea nula (se anulen unas con otras) y el flujo sea cero.

La ley de Gauss resulta muy útil para la resolución de problemas con simetría plana, cilíndrica o esférica.

Potencial y energía eléctrica

Potencial es la circulación del campo eléctrico entre dos puntos y , es decir

$\begin{displaymath} V(\vec{r}_A) - V(\vec{r}_B) = \int^B_A \vec{E}(\vec{r}) \cdot \,d\vec{l}. \end{displaymath}$

(12.2)

Si en esta fórmula multiplicamos ambos miembros por , como $\vec{F}=q\vec{E}$ tendremos que el trabajo eléctrico realizado para desplazar una carga desde una posición hasta otra será simplemente $W_{A\rightarrow B} = q(V(A) -V(B))$ .

Análogamente la energía eléctrica, es decir, la energía potencial eléctrica que tendrá una carga por encontrarse inmersa en un campo eléctrico, será tal que $W_{A\rightarrow B} = E_p(\vec{r}_A) - E_p(\vec{r}_B) = q(V(A) -V(B))$ . Esto supone que

$\begin{displaymath}E_p^e(\vec{r}) = qV(\vec{r}).\end{displaymath}$

$\triangleright$ Tanto la energía como el potencial y el trabajo son magnitudes escalares y por tanto se expresarán como un número normal (con sus correspondientes unidades, eso sí). Además, en virtud del principio de superposición el potencial eléctrico de un conjunto de partículas es la suma del creado por cada uno de ellas. Como el potencial es escalar será tan fácil como sumar sus magnitudes.

Algunos casos particulares de potencial eléctrico

Carga puntual

Usando la ecuación (12.2) con el valor de $\vec{E}$ para una carga puntual, que es $\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r}$ e integrando, se llega fácilmente a la conclusión de que

$\begin{displaymath}V(r) = \frac{1}{4\pi\epsilon_0} \frac{q}{r}.\end{displaymath}$

Campo eléctrico constante

Un sencillo uso de (12.2) nos lleva directamente a la expresión

$\begin{displaymath}V(x) = -Ex,\end{displaymath}$

donde suponemos que el campo $\vec{E}$ es constante, y así el potencial depende de una cierta cantidad unidimensional . Un buen ejemplo sería el campo creado por un plano cargado infinito. En este caso sería la distancia al plano.

Condensadores

Un condensador es un dispositivo capaz de almacenar carga eléctrica. Básicamente están formados por dos conductores situados uno frente al otro, lo más cerca posible, dejando entre medias de ellos un aislante que puede ser el ``vacío'' o un dieléctrico.

Existe una relación de proporción entre el potencial creado entre los dos ``polos''• de un condensador y la carga almacenada. Matemáticamente se puede expresar de una manera simple como

$\begin{displaymath}Q=CV,\end{displaymath}$

donde es la constante de proporcionalidad, denominada capacidad. La unidad de la capacidad es el faradio.

$\diamond$ Un faradio es una unidad muy grande. (Al estilo del culombio). Por ello lo común es encontrarse con microfaradios, nanofaradios o picofaradios.

$\begin{figure}\begin{center} \mbox{ \psfig{file=figuras/condensadores.ps}} \end{center}\end{figure}$

Figura: Asociación de condensadores en serie y en paralelo.

Asociación de condensadores

Serie

En dos condensadores situados en serie, como en el primer gráfico de la figura 12.1 la diferencia de potencial total que cae entre el primero y el segundo será la suma de las diferencias parciales de cada condensador, es decir, $\Delta V_T = \Delta V_1 + \Delta V_2$ . No obstante, al encontrarse unidos en serie la carga de ambos deberá ser igual^12.1, y además será la carga total almacenada por la asociación. Así tenemos que y podemos poner

$\begin{displaymath}\Delta V_t = \Delta V_1 + \Delta V_2 = \frac{Q}{C_1}+\frac{Q}{C_2}\end{displaymath}$

y de aquí se deduce fácilmente que la capacidad efectiva de la asociación es

$\begin{displaymath}\frac{1}{C} = \frac{1}{C_1}+\frac{1}{C_2}.\end{displaymath}$

Paralelo

Si situamos dos condensadores asociándolos en paralelo, como se puede ver en el segundo dibujo de la figura 12.1, tendremos que la diferencia de potencial entre ambos deberá ser igual, y además será la diferencia de potencial total. Esto es así porque tenemos unidos los dos ``polos'' de los condensadores por un conductor, y por tanto la caída de potencial entre los ``polos'' opuestos tiene que ser la misma. A su vez, como cada condensador almacenará una carga distinta, tendremos que para la asociación total

$\begin{displaymath}Q_T = Q_1+Q_2 = C_1\Delta V + C_2\Delta V = (C_1 + C_2) \Delta V.\end{displaymath}$

Se ve pues, de manera sencilla, que la capacidad efectiva o equivalente de dos condensadores asociados en paralelo obedece a la ley

$\begin{displaymath}C = C_1 + C_2.\end{displaymath}$