Movimiento armónico simple

Envia tus archivos, resúmenes, monografías, etc.

Dinámica del sistema. Ecuación del movimiento. Significado de la ecuación. Periodicidad de la ecuación. Velocidad. Aceleración. Energía. Energía cinética. Energía potencial. Energía mecánica. El péndulo simple.

Agregado: 22 de JULIO de 2003 (Por Michel Mosse) | Palabras: 1418 | Votar | Sin Votos | Sin comentarios | Agregar Comentario
Categoría: Apuntes y Monografías > Física >
Material educativo de Alipso relacionado con Movimiento armónico simple

Composición del movimiento armónico simple.: Fórmulas, datos y teoría sobre el movimiento armónico simple (MAS). Aceleración y velocidad angular.

Pendulo Simple.:

Contratos y actas societarias comandita simple:

Enlaces externos relacionados con Movimiento armónico simple

Movimiento armónico simple

Introducción

Hay muchas situaciones en física en las cuales la fuerza que siente una partícula en cierto sistema es proporcional a un desplazamiento respecto cierto punto ``de equilibrio''. Es decir, existen sistemas para los cuales es válida la ley de Hooke

$\begin{displaymath} F=-kx \end{displaymath}$

(13.1)

o al menos, lo es manteniendo el móvil entre ciertos límites. Estos sistemas se dice de ellos que describen un movimiento armónico simple.

La intención de este apartado es estudiar este tipo de movimientos, dada su importancia y su sencillez.

$\diamond$ En todo el estudio que se haga en este capítulo se tratará el problema de manera unidimensional.

$\circ$ Se puede demostrar que la gran mayoría de los sistemas que tiene un punto de equilibrio estable admiten un tratamiento armónico para pequeñas oscilaciones en torno a dicho punto. Esto se puede ver desarrollando en serie de Taylor alrededor del punto y dándose cuenta de que como la primera derivada será nula el primer término que aparecerá será, precisamente, el término de un potencial armónico: $\frac{k}{2}x^2$ .

Dinámica del sistema

Ecuación del movimiento

Si aplicamos la ley de Newton, junto con la ley de Hooke, obtendremos que

$\begin{displaymath}ma=-Kx\ \Rightarrow\ ma+Kx=0.\end{displaymath}$

Esta sencilla ecuación es, no obstante, algo más complicada de resolver que otras anteriores, puesto que las magnitudes involucradas, y dependen La una de la otra, concretamente como $a=\frac{d^x}{dt^2}$

$\begin{displaymath}\frac{d^x}{dt^2} + \frac{K}{m}x=0\end{displaymath}$

que constituye una ecuación diferencial, ya que involucra derivadas de funciones con la propias funciones. Resolver esta ecuación está bastante más allá del ámbito de este curso, pero aún así es fácil darse cuenta de que las funciones $\sin$ y $\cos$ van a tener algo que ver, dado que son las únicas que al ser derivadas dos veces y sumadas consigo mismas dan nulo. Manipulando algunos coeficientes en estas funciones y operando se encuentra la solución más general a este movimiento, que es

$\begin{displaymath} x=A \sin(\omega t + \phi) \end{displaymath}$

(13.2)

y que por tanto constituye la ecuación de movimiento de un sistema que cumpla la ley de Hooke, o bien de un movimiento armónico simple.

Significado de la ecuación

En esta ecuación es la amplitud máxima que puede recorrer el móvil, $\omega$ es la frecuencia angular de la oscilación, es decir, el número de ``radianes'' que da en un segundo. Como parece que la palabra radián no tiene sentido para un muelle, por ejemplo, quizás sea preferible pensar en la frecuencia del movimiento $f=\frac{\omega}{2\pi}$ es decir, el número de oscilaciones completas que da en un segundo, o bien tomar $T=\frac{2\pi}{\omega}$ el periodo de la oscilación, que será el tiempo que tarda nuestro sistema en dar una oscilación completa.

Por último ¿qué será $\phi$ ?. Notemos que, si tomamos tendremos que en el instante 0, el cuerpo que realiza un movimiento estaba en la posición $x=\sin(\phi)$ , por lo que $\phi$ , parámetro al que se conoce con el nombre de fase, nos indica cuando empieza el movimiento.

Periodicidad de la ecuación

Fijándose en la ecuación (13.2) se puede observar que, la existencia de una función seno para describir este movimiento, nos va a llevar irremediablemente hacia un movimiento de tipo periódico. Efectivamente, si tuviéramos un resorte perfecto, este estaría oscilando ``eternamente'' describiendo el mismo movimiento en cada oscilación.

Para adivinar cada cuanto se repite el movimiento bastará igualar el argumento del seno a $2\pi$ , pues como se sabe $\sin(2\pi+\phi)=\sin(\phi)$ . De esta manera tendremos que el movimiento se repetirá, esto es, hará un periodo, cuando $\omega t = 2\pi$ , lo cual supone que el periodo será, como ya habíamos dicho, $T=\frac{2\pi}{\omega}$ .

Es también frecuente describir el movimiento armónico simple como la analogía de una proyección sobre el eje o bien de un movimiento circular de velocidad angular constante $\omega$ .

Velocidad

Para hallar la velocidad que un móvil sometido a una fuerza armónica presenta en un instante basta derivar su ecuación del movimiento. Así tendremos que, como $v=\frac{dx}{dt}$

$\begin{displaymath}v=A\omega\cos(\omega t + \phi),\end{displaymath}$

relación que nos ofrece la velocidad de un movimiento armónico para cualquier instante. Es también común relacionar la velocidad con la posición, cosa sencilla notando que $\cos = \sqrt{1-\sin^2}$ y que, por tanto

$\begin{displaymath}A\omega\cos(\omega t + \phi) = A\omega\sqrt{1-\sin^2(\omega t +\phi)}\end{displaymath}$

de donde, introduciendo la amplitud en la raíz cuadrada

$\begin{displaymath}v=\omega \sqrt{A^2-A^2\sin^2(\omega t + \phi)}\end{displaymath}$

y ahora, echando un vistazo a la relación (13.2) se ve que

$\begin{displaymath}v = \omega\sqrt{A^2-x^2},\end{displaymath}$

siendo esta la relación entre y buscada.

Aceleración

La aceleración a la que se encuentra sometido un móvil que describe un movimiento armónico simple se puede obtener teniendo presente (13.2) y que $a=\frac{d^x}{dt^2}$ . Por tanto

$\begin{displaymath}a=-A\omega^2 \sin(\omega t + \phi).\end{displaymath}$

Si queremos obtener una relación de la aceleración con respecto a la posición del móvil podemos recurrir a observar la similitud entre la ecuación anterior y la que describe la ecuación de movimiento de un m.a.s., o bien utilizando las leyes de Newton y Hooke poner que

$\begin{displaymath}F=ma=-Kx\ \Rightarrow a=-\frac{K}{m} x.\end{displaymath}$

Energía

Energía cinética

Partiendo de la relación de la energía cinética de un móvil, y de la ecuación de velocidad del m.a.s. se tiene que

$\begin{displaymath}E_c = \frac{1}{2} K \cos^2(\omega t + \phi),\end{displaymath}$

o, relacionándolo con la posición

$\begin{displaymath}E_c = \frac{1}{2} K (A^2-x^2).\end{displaymath}$

Energía potencial

¿Es conservativo el movimiento armónico simple? ¿Podemos definir un potencial para él?. La respuesta es sí, por tratarse de una fuerza central^13.1. En este caso ¿cuál será el potencial?. Para hallarlo recordamos que

$\begin{displaymath}W_{A\rightarrow B} = E_p(A)-E_p(B) = \int^B_A F\,dx,\end{displaymath}$

y que, por tanto, tendremos que

$\begin{displaymath}E_p(A)-E_p(B) = \int^B_A -Kx\,dx = \left. -\frac{1}{2}Kx^2\right]^B_A = -\frac{1}{2}KB^2 + \frac{1}{2}KA^2,\end{displaymath}$

siendo ahora ya muy sencillo identificar la energía potencial en una posición como

$\begin{displaymath}E_p(x) = \frac{1}{2}Kx^2.\end{displaymath}$

Energía mecánica

Para obtener la energía mecánica o total puesta en juego en un movimiento armónico simple sumaremos las energías potencial y cinética respecto a la posición. Así tendremos que

$\begin{displaymath}E_T = \frac{1}{2}K(A^2-x^2) + \frac{1}{2}Kx^2 = \frac{1}{2}A^2.\end{displaymath}$

$\diamond$ En el movimiento armónico simple se ve, de una forma que casi roza en lo magistral, lo que la conservación de la energía supone en física. En este caso toda la energía está dada por la fórmula $\frac{1}{2}A^2$ , que es la energía potencial máxima que alcanza el muelle por separarle una distancia de su posición de equilibrio. Más tarde, cuando empieza el movimiento, éste va adquiriendo energía cinética, siempre a costa de su energía potencial, y por tanto acercándose a la posición de equilibrio. Cuando el móvil se encuentra en la posición de equilibrio su energía potencial es nula, pero el cuerpo conserva una cantidad de energía cinética que se irá ahora utilizando en comprimir otra vez el muelle hasta su amplitud máxima, y que contribuirá, por tanto, a incrementar nuevamente la energía potencial. En cualquier caso la suma de ambas nos dará la energía máxima puesta en juego, que se conserva. $\circ$ En un muelle real la conservación de la energía no se cumple, ya que siempre existen pérdidas por rozamiento. Estas pérdidas dan lugar a lo que se denomina un movimiento armónico simple amortiguado, ya que la amplitud va disminuyendo poco a poco, informándonos a su vez de la cantidad de energía que se está perdiendo.

Una forma de solucionar este fenómeno es aportando algo de energía extra al móvil, para contrarrestar la que pierde por rozamiento. Esto puede dar lugar a resonancias y otros fenómenos físicos muy interesantes.

El péndulo simple

Hay ciertos sistemas que, si bien no son estrictamente sistemas sometidos a una fuerza tipo Hooke, si pueden, bajo ciertas condiciones, considerarse como tales. El péndulo simple, es decir, el movimiento de un grave atado a una cuerda y sometido a un campo gravitatorio constante, es uno de ellos.

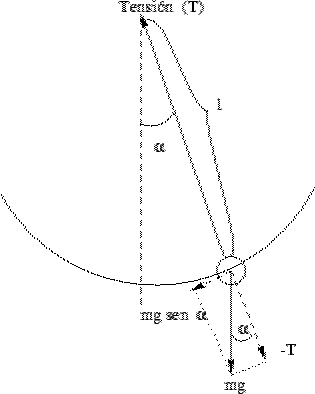
Al colocar un peso de un hilo colgado e inextensible y desplazar ligeramente el hilo se produce una oscilación periódica. Para estudiar esta oscilación es necesario proyectar las fuerzas que se ejercen sobre el peso en todo momento, y ver que componentes nos interesan y cuales no. Esto se puede observar en la figura 13.1.

$\begin{figure}\begin{center} \mbox{ \psfig{file=figuras/pendulo.ps,width=7cm}} \end{center}\end{figure}$

Figura: Descomposición de las fuerzas en un péndulo.

Vemos pues que, considerando únicamente el desplazamiento tangente a la trayectoria, es decir, el arco que se está recorriendo, podemos poner

$\begin{displaymath} ml \frac{d^2\alpha}{dt^2} + mg \sin(\alpha) = 0 \end{displaymath}$

(13.3)

donde no hemos hecho sino aplicar la segunda ley de Newton. Esto se puede ver considerando que el arco es $l \alpha$ y, como es la longitud del hilo y es constante^13.2, la aceleración será $l \frac{d^2\alpha}{dt^2}$ . Por otra parte, aplicando $\sum \vec{F} = m \vec{a}$ , en este caso la fuerza es sólo la de la gravedad, que se descompone en una componente, que se contrarresta con la tensión, más otra, que es la que hace que exista movimiento en la trayectoria marcada por el arco.

Esta ecuación diferencial no es nada fácil de resolver^13.3 y por ello recurrimos a la aproximación siguiente: suponiendo que el ángulo que desplazamos es pequeño, tomamos que $\sin( \alpha) \simeq \alpha$ y así tenemos que

$\begin{displaymath} \frac{d^2\alpha}{dt^2} + \frac{g}{l} \alpha = 0 \end{displaymath}$

(13.4)

que a veces también se expresa como $\ddot{\alpha} + \frac{g}{l} \alpha=0$ .

Esta ecuación es absolutamente análoga a la de un movimiento armónico simple, y por tanto su solución también será (13.2) teniendo, únicamente, la precaución de sustituir el valor de $\omega$ antiguo por el que tiene ahora para un péndulo

$\begin{displaymath}\omega = \sqrt{\frac{g}{l}}.\end{displaymath}$

A partir de aquí se pueden extraer todas las demás relaciones para un péndulo simple, el periodo, frecuencia, etc.