La naturaleza de la luz. Dualidad onda corpúsculo de la materia

Envia tus archivos, resúmenes, monografías, etc.

Introducción histórica. El cuerpo negro. El efecto fotoeléctrico. Descripción del problema. Solución. Efecto Compton. Naturaleza ondulatoria de la materia. Resumen: Dualidad onda-corpúsculo de la luz y la materia.

Agregado: 22 de JULIO de 2003 (Por Michel Mosse) | Palabras: 2586 | Votar | Sin Votos | Sin comentarios | Agregar Comentario
Categoría: Apuntes y Monografías > Física >
Material educativo de Alipso relacionado con naturaleza luz Dualidad onda corpúsculo materia

Ondas Sonoras, Instrumentos de viento y percusión: ...

Ondas: Introducción. Tipos de ondas. Ecuación general de una onda. Ecuación de una onda armónica. Periodo y frecuencia. Longitud de onda y número de ondas. Consideraciones energéticas de las ondas. Energía. Potencia. Intensidad.

Biografia y vida de Xabier Arzalluz: Breve Biografia de Xabier Arzalluz

Enlaces externos relacionados con naturaleza luz Dualidad onda corpúsculo materia

La naturaleza de la luz. Dualidad onda corpúsculo de la materia

Introducción histórica

Históricamente la luz ha sido siempre un ente escurridizo al que los físicos han querido asignar una naturaleza determinada, sin conseguirlo. Newton, a finales del siglo XVII, sostuvo que la luz estaba compuesta por partículas, diferentes según el color, y que ``rebotaban'' en un espejo logrando así explicar porqué los ángulos de incidencia y reflexión eran los mismos. Parece ser que la propagación rectilínea de la luz tuvo mucho que ver con esta posición. Además lograba explicar la refracción sobre la superficie de dos medios diferentes usando también una teoría corpuscular. Huygens, contemporáneo de Newton, hablaba de ondas luminosas, y mediante el principio de Huygens, visto en explicaba también la refracción y reflexión. Según Newton la luz debía ir más rápida en un medio más denso. Según Huygens el fenómeno era al revés, pero no obstante en aquella época aún no se podía medir la velocidad de la luz de manera fiable, y no se levó a cabo ningún experimento para descubrir quien tenía razón; fue la eminencia de Newton lo que decantó la balanza hacia el lado corpuscular de la luz durante esa época, y esta inercia hizo que, pese a los continuos debates y polémicas, fuera la naturaleza corpuscular de la luz la dominante durante el siglo siguiente al de Newton.

A principios del siglo XIX empezó a formarse un sistema consecuente y desarrollado de la luz vista desde un punto ondulatorio. Fueron de gran importancia las aportaciones de Joung y Fresnel. El descubrimiento de muchos fenómenos de difracción e interferencia relacionados con la luz y la posterior explicación del fenómeno ondulatorio de la luz como una onda electromágnetica por parte de Maxwell pareció dejar sentada definitivamente la teoría ondulatoria sobre la luz a finales del siglo XIX.

Pero no obstante a finales del siglo XX surge uno de los fenómenos más complejos y enrevesados estudiados entonces: la radiación del cuerpo negro: un sistema ideal que absorbe toda la radiación que incide sobre él y que, en buena aproximación, puede tomarse como un cuerpo con una cavidad que comunica con el exterior con un pequeño orificio, y cuyas características radiativas cumplen la propiedad de depender sólo de la temperatura de sus paredes.

Fue este hecho el que jugó un papel primordial en la historia de la física moderna y que obligó a Planck (a disgusto, según cuenta la historia) en 1.900 a introducir uno de los fenómenos más sorprendentes de la física: la cuantización de la energía y, en concreto, de la luz.

El cuerpo negro

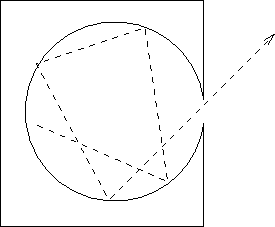
Un esquema de la cavidad que puede aproximarse a un cuerpo negro ideal se encuentra en la figura. Estos cuerpos al irse calentando van encontrando un equilibrio de radiación en el cual, a mayor temperatura, el cuerpo emite a su vez más radiación. Además al irse calentando el cuerpo aumenta la cantidad de energía radiada (de acuerdo con la ley de Stefan-Boltzmann) y la concentración de la energía se desplaza hacia longitudes de ondas más cortas. Precisamente a una representación de la potencia radiada frente a la longitud de onda se le puede denominar distribución de la radiación o distribución espectral.

$\begin{figure}\begin{center} \mbox{ \psfig{file=figuras/cuerpo-negro.ps}} \end{center}\end{figure}$

Figura 18.1: Dibujo de un ``cuerpo negro''.

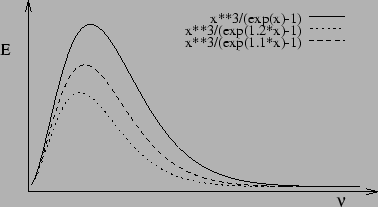
Una gráfica de la distribución espectral de la radiación de un cuerpo negro puede verse en la figura. Este resultado experimental se intentó explicar de una forma directa a partir de la termodinámica clásica, y el resultado obtenido, que también está representado en la figura, claramente no coincidía con el resultado ``verdadero'', que es siempre el que marca la experiencia de laboratorio.

ectro-radiacion.ps}} \end{center}\end{figure}" style='width:283.5pt;height:155.25pt'> $\begin{figure}\begin{center} \mbox{ \psfig{file=figuras</div> <hr size=1> <a name=$

Votar

Ingresar una calificación para del 1 al 10, siendo 10 el máximo puntaje.

Para que la votación no tenga fraude, solo se podrá votar una vez este recurso.

Comentarios de los usuarios

Agregar un comentario:

Aún no hay comentarios para este recurso.

Sobre ALIPSO.COM

Monografias, Exámenes, Universidades, Terciarios, Carreras, Cursos, Donde Estudiar, Que Estudiar y más: Desde 1999 brindamos a los estudiantes y docentes un lugar para publicar contenido educativo y nutrirse del conocimiento.

Contacto »

Participá

Legales

Contacto

Teléfono: +54 (011) 3535-7242
Email:

Formulario de Contacto Online »

ectro-radiacion.ps}} \end{center}\end{figure}" border=0 v:shapes="_x0000_i1026">

Figura: Distribución espectral de la radiación emitida por un cuerpo negro a distintas temperaturas.

En 1900 el físico alemán, Max Planck afirmó que realizando una inusitada modificación de los cálculos clásicos, e introduciendo una hipótesis nueva y singularmente extraña, había encontrado una distribución espectral que explicaba perfectamente los datos experimentales.

Esta ``sorprendente hipótesis'' era que la energía emitida y absorbida por el cuerpo no era continua, es decir, el cuerpo no podía tomar o dejar cualquier valor de ésta, sino discreta y además, proporcional a la frecuencia. Es decir

$\begin{displaymath} E=h\nu \end{displaymath}$

(18.1)

donde es la constante de proporcionalidad, de valor $h06.626\cdot 10*^{-34}Js$ y conocida actualmente como constante de Planck.

Planck fue absolutamente incapaz de encajar esta hipótesis dentro del marco de la mecánica clásica y, sin proponérselo, había dado el primer paso para el advenimiento de la mecánica cuántica.

$\triangleright$ La radiación electromagnética se emite en ``paquetes'' de energía o fotones cuyo valor energético es:

$\begin{displaymath}E=h\nu.\end{displaymath}$

El efecto fotoeléctrico

Descripción del problema

Este efecto fue descubierto por Hertz en 1.887 y estudiado por Lenard en 1.900. Fue satisfactoriamente explicado por Einstein en 1.905 y su explicación le supuso ganar el Premio Nobel de Física. El efecto fotoeléctrico consiste en el hecho de que, cuando se ilumina una superficie metálica limpia, bajo ciertas condiciones se emiten electrones. Estos electrones pueden ser recogidos en un tubo de rayos catódicos para relacionar su emisión con algo fácilmente medible, como es la intensidad y voltaje eléctrico.

Analicemos que sucede en el circuito de la figura. Cuando la luz incide sobre el cátodo C se emiten electrones. Si alguno de ellos choca con el ánodo A existirá una cierta corriente por el circuito. El número de electrones emitidos que alcanzan el ánodo puede variarse haciendo el ánodo positivo o negativo respecto el cátodo, es decir, creando una diferencia de potencial entre ellos. Cuando es positivo los electrones arrancados por la luz son atraídos por el ánodo. Para un valor lo suficientemente alto de todos los electrones ``arrancados'' por la luz alcanzan el ánodo y la corriente logra su valor máximo; si aumentamos más descubriremos que que la corriente ya no aumenta, se mantiene en su valor máximo, ya que no influye en que se liberen más electrones del cátodo, sino sólo en que todos los que son liberados se acerquen hacia el ánodo. Si variamos al revés los electrones serán repelidos por el ánodo, y sólo aquellos que tengan una energía cinética ( $\frac{1}{2}mv^2$ ) suficientemente alta lograrán llegar al ánodo y generar corriente. Pero ahora bien, cuando bajamos y lo hacemos menor que un cierto valor no existe corriente alguna, lo cual significa que ningún electrón alcanza el ánodo. Entonces este potencial estará relacionado con la máxima energía cinética que tendrán los electrones, de manera que podemos poner

$\begin{displaymath}\frac{1}{2}mv^2\vert _{max} = eV_0.\end{displaymath}$

$\begin{figure}\begin{center} \mbox{ \psfig{file=figuras/efecto-fotoelectrico.ps}} \end{center}\end{figure}$

Figura: Dispositivo simplificado para la medición del efecto fotoeléctrico.

Ahora bien ¿y qué es lo interesante de esta experiencia?. Lo curioso es que el valor de no depende de la intensidad de la radiación, pero si depende de ``algo tan peregrino'' como el color de la luz con que se ilumine el cátodo. Así pues aparentemente al aumentar la intensidad, por tanto la energía por unidad de tiempo que cae sobre el cátodo, no aumenta la energía cinética de los electrones emitidos. ¿Cómo se puede explicar esto?. ¿Por qué sucede?. Estas fueron las preguntas que se hizo Einstein ( y logró contestar) en 1.905.

Solución

Einstein demostró que estas experiencias podían entenderse suponiendo que la energía luminosa no se distribuye de manera continua, como dice el modelo clásico ( y Maxwelliano) de la luz, sino cuantizada en paquetes pequeños llamados fotones. La energía de un fotón es $E=h\nu$ , la relación que Planck usó para la explicación del cuerpo negro. Einstein supuso que un electrón emitido desde la superficie del cátodo es de alguna forma ``arrancado'' por el impacto con el fotón, de forma que toda la energía del fotón pasa al electrón. Ahora bien, el electrón recibe su energía de un único fotón. Así, cuando se aumenta la intensidad de la luz lo que sucede es que al incidir más fotones sobre el cátodo por unidad de tiempo quedan más electrones liberados, pero la energía que ha absorbido cada electrón no varía, es la misma.

De esta manera se hace un sencillo cálculo energético: Si la energía necesaria para que se desprenda un electrón de la superficie de un metal es, pongamos, una cierta , la energía máxima de los electrones debería ser la que queda de la que tenía el electrón, es decir

$\begin{displaymath}\frac{1}{2}mv^2\vert _{max} = h\nu - W\end{displaymath}$

y como a su vez, sabíamos que esta energía era podemos deducir que este potencial de frenado será

$\begin{displaymath}V= \frac{h\nu - W}{e}.\end{displaymath}$

Este resultado coincidía plenamente con los datos experimentales, y además el valor de la constante resultó ser igual que el usado por Planck para explicar el cuerpo negro. Esto supuso una nueva evidencia sobre la validez universal de la hipótesis de la cuantificación de la energía lumínica.

Efecto Compton

Arthur H. Compton, en 1.923 realizó una experiencia en la que se enviaban rayos X (un tipo de luz más energética que la visible) a una zona con átomos, y posteriormente se medía tanto la frecuencia y ángulo de la luz dispersada como la velocidad el electrón derivado tras el choque. Utilizando los principios de conservación de la energía y del momento lineal en estos choques, todos los resultados eran coherentes si se suponía que la luz se comportaba como una partícula (un fotón) que colisiona con el electrón, con energía dada por la relación de Planck $E=h\nu$ y con momento lineal igual a

$\begin{displaymath} p=\frac{h}{\lambda}. \end{displaymath}$

(18.2)

$\diamond$ Puede resultar útil recordar que, de acuerdo con la teoría clásica, la energía y cantidad de movimiento de una onda electromagnética está marcada por

$\begin{displaymath}E=pc,\end{displaymath}$

entonces, relacionando esta mediante la ecuación y recordando que $c=\lambda \nu$ se obtiene fácilmente ).

Naturaleza ondulatoria de la materia

Las ideas de simetría, que se muestran siempre muy útiles en la física, levaron a Louis de Broglie a pensar que, al igual que la luz, pese a ser de naturaleza supuestamente ondulatoria, presentaba muchas veces una componente corpuscular, podía ser que la materia normal, tratada siempre como partícula, tuviese también una naturaleza ondulatoria.

Pero de Broglie fue más allá: si el momento lineal de un fotón, según el experimento de Compton, era $p=\frac{h}{\lambda}$ ¿por qué no utilizar esta relación para encontrar la ``longitud de onda de la materia''?. Esto es, para un cuerpo normal y usando y despejando así $\lambda$ obtenemos

$\begin{displaymath} \lambda=\frac{h}{mv}. \end{displaymath}$

(18.3)

Ahora bien, la física tiene siempre una forma para decidir cuando una hipótesis es o no correcta: la experimentación. En experiencias posteriores se pudo comprobar que efectivamente, partículas como los electrones, pueden producir patrones de difracción, un hecho puramente ondulatorio, similares a los que producen los rayos X.

Ahora bien, si todas las partículas presentan esta dualidad onda y corpúsculo, ¿por qué en nuestra vida cotidiana no vemos, por ejemplo, la difracción de una bola de billar o de algún objeto igualmente macroscópico?. La respuesta es que, si tomamos una bola de billar con una masa de gramos y una velocidad de $1\frac{m}{s}$ su longitud de onda será, dado el ínfimo valor de , extremadamente pequeña, razón por la cual con los aparatos actuales somos incapaces de comprobar su existencia. Para objetos más pequeños (protones, electrones, neutrinos...) se ha encontrado un comportamiento ondulatorio siempre que se ha buscado.

$\circ$ Evidentemente toda esta serie de fenómenos nuevo invalida de tal manera las leyes anteriores que es necesaria la búsqueda de nuevas ``leyes de Newton'', de nuevas ecuaciones que sean capaces de explicar a su vez estos nuevos fenómenos. Estas nuevas leyes entran a formar parte de un nuevo marco de la física que se conoce como Física Cuántica o Mecánica Cuántica. La palabra cuántica hace referencia al hecho de que, en este nuevo marco, algunas magnitudes no van a ser continuas, sino que van a ser discretas, a estar cuantizadas, es decir, a permitir sólo ciertos valores discretos.

Podemos citar a los físicos Schr�dinger, Heisemberg y Pauli como los padres de la mecánica cuántica, descubridores a su vez respectivamente de la mecánica de matrices, la ecuación de Schr�dinger de la Mecánica Cuántica y la ecuación de Pauli de la Mecánica Cuántica y Relativista (en la cual aparece de manera natural el fenómenos del espín), pero toda lista sería incompleta. La Mecánica Cuántica y la Mecánica Relativista son dos espectaculares teorías, en su mayoría poco intuitivas e incluso muchas veces ``contra el sentido común'' que han revolucionado la física del siglo XX y han logrado explicar infinidad de hechos nuevos y otros ya conocidos bajo una luz diferente. Su unión con las teorías de campos, en lo que se conoce como Teoría Cuántica de Campos ha dado pie a una de las teorías más exactas y extrañas que existen actualmente.

Tecnológicamente aparatos tan cotidianos como los ordenadores o avances médicos como la radiología no habrían sido posibles sin estos descubrimientos.

Resumen: Dualidad onda-corpúsculo de la luz y la materia

Así pues como resumen ¿qué es la luz y la materia? ¿Son ondas o son partículas? ¿Se comportan como las primeras o las segundas?. Como se ha podido ir desgajando a lo largo de las secciones la respuesta no es fácil. La física en sí misma no es una ciencia que pretenda explicar la esencia de la Naturaleza, sino más bien cómo se comporta ésta. Por eso la contestación a la pregunta de si la luz es onda o es partícula es irrelevante. Lo importante es que, según la experiencia, se comporta de una u otra forma en unos u otros casos. Así mismo la materia se comporta como onda o como corpúsculo según la ocasión. Sería como si ``fuera onda los lunes miércoles y viernes y partícula el resto''.

No obstante quizás esta explicación parezca muy absurda a muchos, que piensen que todo esto tiene que estar claramente equivocado porque ¿cómo va a ser algo onda y partícula a la vez?. Según los más elementales principios de la lógica algo no puede ser y no ser a la vez, o bien un ente no puede contener dos propiedades contradictorias de forma consecutiva.

El problema surge al considerar la esencia misma de la concepción ``onda'' o de la concepción ``partícula''. La mente humana crea un modelo, un concepto como ``onda'' para explicar una serie de hechos, y luego renuncia a los hechos para afirmarse más en la concepción de ``onda''. Análogamente crea la concepción ``partícula''. Posteriormente cree que, el hecho de que ciertos aspectos de la Naturaleza puedan explicarse como partícula implican que ese aspecto es una partícula, y esta identificación es la que resulta incorrecta. Por ejemplo: una bola de billar se comporta como una partícula, pero esto no significa que sea una partícula. ¿Qué es por tanto una bola de billar?. No es la física quien tiene que dar la respuesta, entre otras cosas porque (es mi opinión) ni es un tema de su incumbencia ni lo podrá saber nunca. La bola de billar es un objeto incognoscible al que podemos asociar una etiqueta ``partícula'' porque en todas las ocasiones se comporta como tal, pero por ello no tiene por qué ser una partícula. Dicho de otra forma, ``onda'' o ``partícula'' son sólo modelos o categorías mentales, y la Naturaleza no tiene porqué amoldarse a nuestras aldeanas categorías mentales. La Naturaleza será lo que sea, y muchas facetas suyas se aproximarán a ``onda'' y otras a ``partícula'' que no son más que aproximaciones o modelos humanos.

Así pues ¿qué es un fotón? ¿Qué es la luz?. Conocer la esencia de la luz no es tarea de la física, su tarea es describir cómo se comporta la luz bajo ciertas condiciones. Y de esta forma se descubre y estudia que a veces se comporta como luz y a veces como partícula, pero ``comportarse como'' es muy distinto de ``ser''.

Aún así sería interesante concluir citando unas palabras de Einstein: Lo mas incomprensible es que sea comprensible.