Tablas y fórmulas útiles

Envia tus archivos, resúmenes, monografías, etc.

Introducción. Cálculo complejo. Cálculo vectorial. Funciones elementales. Trigonométricas. Logarítmicas y exponenciales. Derivación. Propiedades generales. Tabla de derivadas. Integración Definición y propiedades. Tabla de integrales.

Agregado: 22 de JULIO de 2003 (Por Michel Mosse) | Palabras: 165 | Votar | Sin Votos | Sin comentarios | Agregar Comentario
Categoría: Apuntes y Monografías > Física >
Material educativo de Alipso relacionado con Tablas fórmulas útiles

Para hallar las fórmulas mínimas de manera más fácil utilizamos los números de oxidación. La suma algebraica de los números de oxidación debe dar como resultado 0.: Apuntes de Química. CNBA. Clases de Gravano, 2003.

IUPAC- Formulas- Petroleo. 21-5-98 / 5°3°:

Operaciones con arboles, tablas, arboles-2-3, b-arboles y operac: ...

Enlaces externos relacionados con Tablas fórmulas útiles

Tablas y fórmulas útiles

Introducción

Este apéndice está pensado como un complemento o un recordatorio matemático de algunos conceptos de esta índole imprescindibles para abordar con éxito el estudio de la física. No obstante, si el lector descubre que desconoce una gran parte del contenido de este apéndice, o bien que no comprende la procedencia de las fórmulas, debería por su cuenta estudiar estas bases hasta su total comprensión.

Cálculo complejo

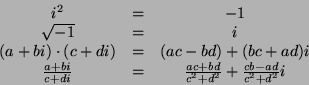
$\begin{displaymath}\begin{array}{ccc} i^2 & = & -1 \\ \sqrt{-1} & = & i \\ (a+... ... & \frac{ac+bd}{c^2 + d^2} + \frac{cb-ad}{c^2+d^2}i \end{array}\end{displaymath}$

Cálculo vectorial

Módulo

$\left\vert\vec{a}\right\vert = \sqrt{a_x^2+a_y^2+a_z^2}$ .

Producto escalar

$\vec{a} \cdot \vec{b} = ab\cos \theta$ .

Producto vectorial

Ver 4.3.4.

Funciones elementales

Trigonométricas

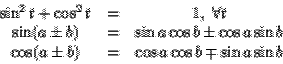
$\begin{displaymath}\begin{array}{ccc} \sin^2 t + \cos^2 t &=& 1,\ \forall t \\ ... ...cos (a\pm b) & = & \cos a \cos b \mp \sin a \sin b \end{array}\end{displaymath}$

Logarítmicas y exponenciales

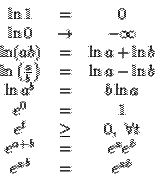
$\begin{displaymath}\begin{array}{ccc} \ln 1 & = & 0 \\ \ln 0 & \rightarrow & -\... ... t\\ e^{a+b} & = & e^ae^b \\ {e^a}^b & = & e^{ab} \end{array}\end{displaymath}$

Derivación

Propiedades generales

Constante

$\frac{d}{dt}K = 0$ .

Suma

$\frac{d}{dt}(f+g) = \frac{d}{dt}f + \frac{d}{dt}g$ .

Producto por constante

$\frac{d}{dt}(Kf) = K\frac{d}{dt}f$ .

Producto

$\frac{d}{dt}(f\cdot g) = \left( \frac{d}{dt}f \right) g + f \left( \frac{d}{dt}g \right)$ .

División

$\frac{d}{dt}\frac{f}{g} = \frac{\left( \frac{d}{dt}f \right) g - f \left( \frac{d}{dt}g \right)}{g^2}$ .

Regla de la cadena

$\frac{d}{dt}f(g(t)) = (\frac{d}{dt}f )(g(t)) \cdot \frac{d}{dt}g(t)$ .

Ejemplo de la regla de la cadena

$\frac{d}{dt}\sin(t^2) = \cos(t^2)2t$ .

Tabla de derivadas

$\begin{displaymath}\begin{array}{cc\vert cc} \hline f(t) & \frac{d}{dt}f(t) & f(... ...{t^2-1}} & \arg \tanh t & \frac{1}{1-t^2}\\ \hline \end{array}\end{displaymath}$

Integración

Definición y propiedades

Se define $\int f(t) dt = F(t) + C$ si se cumple que $\frac{d}{dt}F(t) = f(t)$ . Algunas propiedades son:

Nula

$\int 0 dt = C$ donde es una constante cualesquiera.

Constante

$\int K f(t) dt = K \int f(t) dt$ ,

Suma

$\int\left( f(t) + g(t)\right) dt = \int f(t) dt + \int g(t)dt$ .

La integral de un producto de dos funciones es

$\begin{displaymath}\int u(t)dv(t) = u(t) v(t) - \int v(t) du(t). \end{displaymath}$

Tabla de integrales

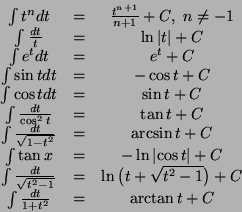
$\begin{displaymath}\begin{array}{ccc} \int t^n dt & = & \frac{t^{n+1}}{n+1} + C,... ...) + C \\ \int \frac{dt}{1+t^2} & = & \arctan t + C \end{array}\end{displaymath}$