- TEMA 2 -

LENGUAJES FORMALES 

1.- Alfabetos

Se llama alfabeto a un conjunto finito, no vacío, cuyos elementos se denominan "letras" o "símbolos". Se definen los alfabetos por la enumeración de los símbolos que contiene. Veamos algunos ejemplos :

A1={A, B, C, D, E, F , G, ..., Z}

A2={0,1}

A3={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, .}

A4={\, /}

2.-Palabras

Se denomina palabra, formada con los símbolos de un alfabeto, a toda secuencia finita de letras de ese alfabeto.

Palabras sobre A1 :

JUAN, PEDRO, LUIS, DASDSADA

Palabras sobre A2 :

0 1 11001100 1111

Palabras sobre A3 :

2 304 126.34

Palabras sobre A4 :

\\\\/// /\//

Se usarán letras minúsculas para representar las palabras de un alfabeto :

x = JUAN (sobre A1)

y = //\/ (sobre A4)

z = 123.56 (sobre A3)

La longitud de una palabra viene determinada por el número de símbolos (letras) que la componen :

| x | = 4

| y | = 4

| z | = 6

Se define la palabra vacía como aquella cuya longitud es cero. Se representa mediante la letra l. Cualquiera que sea el alfabeto considerado, siempre puede formarse con sus símbolos la palabra vacía (bastaría formar una palabra sin seleccionar a ninguno de ellos).

El conjunto de palabras que se pueden formar con las letras de un alfabeto recibe el nombre de "universo del discurso" o "lenguaje universal" de ese alfabeto. Sobre el alfabeto A, el lenguaje universal se representa por W(A). Evidentemente W(A) es un conjunto infinito.

Supongamos el alfabeto con el menor número posible de letras (1).

A = { p }

En este caso, W(A) = { l, p, pp, ppp, pppp, ppppp, ...}, y contiene un número infinito de elementos.

La palabra vacía pertenece a todos los lenguajes universales de todos los alfabetos posibles.

3.- Operaciones con palabras

•       Concatenación de palabras

Sean dos palabras x, y tales que

x � W(A), y � W(A)

Supongamos que | x | = i y que | y | = j. Así x será A_m1A_m2A_m3 ... A_mi e y será A_n1A_n2A_n3 ... A_nj. Se llama concatenación de las palabras x e y (y se representa por xy) a otra palabra (z) obtenida poniendo las letras de y a continuación de las de x :

z= {A_m1A_m2A_m3 ... A_mi A_n1A_n2A_n3 ... A_nj}

|--------------------------------|-----------------------|

x y

Otra notación habitual para la operación de concatenación de las palabras x e y es x.y.

Consideramos a continuación las propiedades de la concatenación :

•       Operación cerrada. Es decir, la concatenación de dos palabras de W(A) es otra palabra de W(A). Si x � W(A) e y � W(A), entonces xy � W(A).

•       Propiedad asociativa : x(yz)=(xy)z

Por cumplir estas propiedades, la operación de concatenación de palabras de un alfabeto es un semigrupo.

•       Existencia de elemento neutro. El elemento neutro de esta operación es la palabra vacía l, tanto por la derecha como por la izquierda. Siendo x una palabra cualquiera, se cumple :

xl = lx = x

Al cumplir las tres propiedades anteriores, se trata de una operación con estructura de monoide (semigrupo con elemento neutro).

Sin embargo, la concatenación no cumple la propiedad conmutativa. Esto se observa mediante cualquier contraejemplo. Sean las palabras x= ABC e y = CDE. Tenemos que

xy = ABCCDE

yx = CDEABC

Si z está formada por la concatenación de las palabras x e y (es decir, z = xy), se dice que x es cabeza de z y que y es cola de z. Además, x será cabeza propia siempre que y no sea la palabra vacía. De igual manera, y será cola propia de z siempre que x no sea la palabra vacía.

Si x = ABC, las siguientes palabras son cabeza de x : l, A, AB, ABC. Todas ellas son propias excepto ABC. Colas de x serán : l, C, BC y ABC. Todas ellas propias excepto ABC.

La función longitud de una palabra tiene, respecto a la concatenación, propiedades semejantes a las de la función logaritmo respecto de la multiplicación :

| xy | = | x | + | y |

Sea un alfabeto S. Cada una de sus letras puede considerarse como una palabra de longitud 1, perteneciente a W(S). Si a estas palabras elementales se les aplica la concatenación, puede formarse cualquier palabra de W(S), excepto la palabra vacía. Se dice entonces que S es un conjunto de generadores de W(S) - l.

Este conjunto, junto con la operación de concatenación, es un semigrupo, pero no un monoide, ya que carece de elemento neutro.

Si se añade la palabra vacía a W(S), entonces se convierte en monoide libre generado por S.

Todo monoide libre cumple la ley de "cancelación izquierda", ya que para todo a,b,c � W(S) se cumple que

ab = ac � b = c

•       También se cumple en este caso la ley de "cancelación derecha" :

ac = bc � a = b

•       Potencia de una palabra

Se trata de una nueva notación para reducir algunos casos de la operación anterior. Se denomina potencia i-ésima de una palabra a la concatenación consigo misma i veces. Al poseer la concatenación la operación asociativa, no es necesario especificar el orden en que efectuar las concatenaciones.

xⁱ = xxx...xx

|----------|

i

Evidentemente x¹ = x

También resulta evidente que se cumplen las siguientes relaciones

xⁱ⁺¹ = xⁱx = x xⁱ (i > 0)

xⁱ x^j = x^i+j (i, j > 0)

Para que ambas relaciones se cumplan también para i, j = 0, basta con definir x⁰ = l, cualquiera que sea x.

Supongamos que x = CHJK, entonces

x² = xx = CHJKCHJK

____ ____

x³ = xxx = CHJKCHJKCHJK

____ ____ ____

Las propiedades de la función longitud también son semejantes a las del logaritmo, ya que

| xⁱ | = i | x |

•       Reflexión de palabras

Sea x = A₁A₂A₃ .... A_n, se denomina palabra refleja o inversa de x, representado por x^-1, a

x^-1 = A_nA_n-1 .... A₃A₂A₁

Es decir, esta palabra está formada por las mismas letras, pero ordenadas de forma inversa. La función longitud es invariante con respecto a la reflexión de palabras :

| x^-1 | = | x |

4.- Lenguajes

Se denomina lenguaje sobre el alfabeto S a cualquier subconjunto del lenguaje universal W(S).

L � W(S)

El conjunto vacío, f ,es un subconjunto de W(S). Este lenguaje no debe confundirse con aquel que contiene únicamente a la palabra vacía. Para diferenciarlos hemos de darnos cuenta de la distinta cardinalidad de ambos conjuntos, ya que

c (f) = 0

y

c ({l}) = 1

Estos dos conjuntos serán lenguajes sobre cualquier alfabeto. El alfabeto en sí puede considerarse como un lenguaje : el formado por todas las posibles palabras de una letra.

5.- Operaciones con lenguajes

•       Unión de lenguajes

Consideremos dos lenguajes diferentes definidos sobre el mismo alfabeto

L₁ � W(S) y L₂ � W(S)

Se denomina unión de ambos lenguajes, L₁ É L₂, al lenguaje definido de la siguiente forma :

{ x | x � L₁ ó x � L₂}

Según se observa es el conjunto formado por las palabras de ambos lenguajes.

Consideremos las propiedades de esta operación :

•       Operación cerrada. La unión de dos lenguajes definidos sobre el mismo alfabeto será otro lenguaje definido sobre ese alfabeto

•       Propiedad asociativa. (L₁ É L₂) É L₃ = L₁ É (L₂ É L₃)

•       Existencia de elemento neutro. Cualquiera que sea el lenguaje L, se cumple que L É f = f É L = L

Por cumplir las propiedades anteriores, esta operación posee la estructura de monoide libre.

•       Propiedad conmutativa. Cualesquiera que sean los lenguajes L₁ y L₂, se verifica que L₁ É L₂ = L₂ É L₁

•       Propiedad de idempotencia. Cualquiera que sea el lenguaje L, se verifica que L É L = L.

•       Concatenación de lenguajes

Consideremos dos lenguajes definidos sobre el mismo alfabeto, L₁ y L_2..Se denomina concatenación o producto de estos lenguajes al lenguaje definido así :

{ xy | x � L₁ y x � L₂}

Es decir, todas las palabras de este lenguaje estarán formadas al concatenar cada una palabra del primero de los lenguajes con otra del segundo.

La definición anterior sólo es válida si L₁ y L₂ contienen al menos un elemento. La extensión de la concatenación de lenguajes al lenguaje vacío se hace de la siguiente manera :

fL = Lf = f

Con respecto a las propiedades de esta operación :

•       Operación cerrada. La concatenación de lenguajes sobre el mismo alfabeto es otro lenguaje sobre ese alfabeto.

•       Propiedad asociativa. (L₁ L₂) L₃ = L₁ (L₂ L₃)

•       Elemento neutro. Cualquiera que sea el lenguaje considerado, el lenguaje de la palabra vacía cumple que {l} L = L {l} = L

Por cumplir estas propiedades, la concatenación de lenguajes posee la estructura de monoide.

•       Potencia de un lenguaje

Al igual que ocurría con esta operación sobre palabras, se trata de una notación para reducir algunos casos de la operación anterior.

Se define la potencia i-ésima de un lenguaje a la operación de concatenarlo consigo mismo i veces. Al poseer esta operación la propiedad asociativa, no es necesario especificar el orden en que se efectuarán las operaciones.

Lⁱ = LLL ....L

|----------|

i

Evidentemente L¹ = L

También resulta evidente que se cumplen las siguientes relaciones

Lⁱ⁺¹ = LⁱL = L Lⁱ (i > 0)

Lⁱ L^j = L^i+j (i, j > 0)

Para que ambas relaciones se cumplan también para i, j = 0, basta con definir L⁰ = {l}, cualquiera que sea L.

•       Clausura positiva de un lenguaje

Se define la clausura positiva de un lenguaje L como :

_�

L⁺ = É Lⁱ

ⁱ⁼¹

Se trata del lenguaje obtenido uniendo el lenguaje con todas sus potencias posibles, excepto L⁰. Si L no contiene la palabra vacía, la clausura positiva tampoco la contendrá.

Ya que cualquier alfabeto � es un lenguaje sobre él mismo (formado por las palabras de longitud 1), se le puede aplicar esta operación. Se observa entonces que

�⁺ = W(�) - {l}

•       Iteración, cierre o clausura de un lenguaje

Se define la iteración, cierre o clausura de un lenguaje L como :

_�

L^* = É Lⁱ

ⁱ⁼⁰

Se trata del lenguaje obtenido uniendo el lenguaje con todas sus potencias posibles, incluso L⁰. Obviamente todas las clausuras contienen la palabra vacía.

Son evidentes las siguientes relaciones :

L^* = L⁺ É {l}

L⁺ = L L^* = L^* L

(Con respecto a la segunda relación, hay que considerar que es el resultado de concatenar L con L^*. Por tanto, cada nueva palabra de este lenguaje estará formada por la concatenación de una palabra de cada uno de los lenguajes. Al pertenecer la palabra vacía a L^*, se concatenará con las palabras de L (ninguna es la palabra vacía) y como resultado de la concatenación será imposible obtener la palabra vacía).

Ya que el alfabeto S es un lenguaje sobre sí mismo, puede aplicársele esta operación. Se verá entonces que

�^* = W(�)

Conocida esta notación, se denominará �^* al lenguaje universal o "universo del discurso" sobre el alfabeto �.

•       Reflexión de lenguajes

Sea L un lenguaje cualquiera. Se llama lenguaje reflejo o inverso de L, representándose por L^-1 a

{ x^-1 | x � L }

Es decir, se trata de un lenguaje que contiene las palabras inversas a las palabras de L.

6.- Contexto válido

Sea S un alfabeto y L un lenguaje sobre él ( L � �^*) y x � �^* una palabra cualquiera (no es necesario que sea una palabra perteneciente al lenguaje L). Se dice que el par de palabras u y v

u, v � �^*

son un contexto válido de x en L, si se cumple que

uxv � L

•       Si (u , l) es un contexto válido de x, se dice que u es un prefijo válido de x.

•       Si ( l , v) es un contexto válido de x, se dice que v es un sufijo válido de x.

Ejemplo : Sea S = {0 , 1}, L = { y| | y| = 4}. Sea la palabra x = 01. Consideremos el conjunto de contextos válidos de x :

(0,0), (0,1), (1,0), (1,1), (l,00), (l,01), (l,10), (l,11), (00, l),

(01, l), (10, l), (11, l)

Sea z = 0101. El único contexto válido para z, con relación al lenguaje anterior, es (l,l).

En el caso en que z = 011011, no existe ningún contexto válido de esta palabra, con relación al lenguaje L.

Se pueden definir dos relaciones de equivalencia sobre los elementos de �^*, P_L y S_L.

Se dice que x P_L y si x e y tienen el mismo conjunto de prefijos válidos. De la misma forma, se dice que x S_L. y si ambas palabras poseen el mismo conjunto de sufijos válidos.

Sea x S_L. y. Se demostrará entonces que xz S_L. yz, " z � �^*.

Se cumple que xz(u) � L � x(zu) � L � y(zu) � L � (yz)u � L

Partimos de suponer que u es un sufijo válido de xz (lo que significa que xz(u) � L). Por la aplicación de la propiedad asociativa sobre la operación de concatenación, resulta obvio que se obtiene la misma palabra independientemente del orden en que se efectúen las operaciones de concatenación. Es decir xz(u) es la misma palabra que x(zu). Al estar x e y relacionadas mediante S_L, y al ser zu un sufijo válido de x, en L, será éste también un sufijo válido para y. Esto no quiere decir más que y(zu) pertenece al lenguaje L. Además, por la aplicación de la operación de concatenación, resulta que y(zu) es la misma palabra que yz(u). De esta forma vemos que u es un contexto válido para yz. Con lo cual, se ha demostrado la afirmación anterior.

Es decir, (xz) e (yz) tienen los mismos sufijos válidos. Por tanto

x S_L. y � xz S_L. yz

Por lo visto anteriormente, la relación S_L es compatible por la derecha con la operación de concatenación. Igual ocurre con la relación P_L por la izquierda.

7.- Producciones

Sea � un alfabeto. Se llama producción a un par ordenado (x,y), donde tanto x como y pertenecen a �^*. Se dice que x es la parte izquierda de la producción, e y la derecha.

Las producciones se denominan también reglas de escritura, o reglas de derivación. Es frecuente representarlas de la siguiente manera :

x ::= y

•       Derivación directa

Sea � un alfabeto y x ::= y una producción sobre las palabras de ese alfabeto. Sean v y w dos palabras del mismo alfabeto (v, w pertenecen a �^*). Se dice que w es derivación directa de v, o que v produce directamente a w o que w se reduce directamente a v, lo que se representa de la siguiente manera

v � w

si existen dos palabras z, u � �^*, tales que

v = zxu

w = zyu

Como consecuencia directa de la definición de derivación directa, si x ::= y es una producción sobre el alfabeto S, entonces x�y, ya que :

x = lxl

y = lyl

Ejemplo : vamos a considerar el alfabeto constituido por todas las letras mayúsculas

S = { A, B, C, D, E ....... Z }, y consideramos la regla de derivación ME ::= BA. Es fácil comprobar que CAMELLO � CABALLO, ya que

v = CAMELLO = CA ( ME ) LLO = zxu

w = CABALLO = CA ( BA ) LLO = zyu

Sobre el alfabeto S definiremos un conjunto de producciones, llamado P. Sean v y w dos palabras definidas sobre ese alfabeto (v, w � S^*). De forma análoga a como se había comentado con anterioridad, se dice que w deriva directamente de v, o que v produce directamente a w, o que w se reduce directamente a v, si existen dos palabras z y u (pertenecientes a S^*) , tales que

v = zxu

w = zyu

donde x ::= y es cualquiera de las producciones del conjunto P.

Ejemplo : consideremos el alfabeto S = { 0, 1, 2, D, P } y las siguientes producciones

(1)D ::= PD (2)D :: P (3)P ::= 0 (4)P ::= 1

(5)P ::= 2

Vamos a presentar algunas derivaciones :

D � PD (1)� PPD (1)� PPPD (1)� PPPP (2)� PP1P (4)� PP12 (4)� P012 (3)�1012 (4)

Entre paréntesis se muestra la producción que se ha aplicado en cada caso.

•       Derivación

Sea S un alfabeto y sea P un conjunto de producciones sobre las palabras de ese alfabeto. Sean v y w dos palabras de ese mismo alfabeto (v, w � S^*). Se dice que w deriva de v o que v produce a w o que w se reduce a v , y se expresa mediante v �+ w, si existe una secuencia finita de palabras u₀, u₁, u₂, u₃, ..... u_n (n > 0), tales que

v � u₀

u₀ � u₁

u₁ � u₂

u₂ � u₃

u₃ � u₄

............

u_n-1 � u_n

u_n � w

La derivación anterior tiene una longitud de n+2, ya que estas son las producciones que hemos tenido que aplicar hasta llegar a obtener w a partir de v.

De las definiciones de derivación directa y derivación se deduce que si v � w entonces v �+ w, mediante una secuencia de derivaciones de longitud 1.

•       Relaciones de Thue

Sea S un alfabeto y sea P un conjunto de producciones sobre las palabras de ese alfabeto. Sean v y w dos palabras del mismo alfabeto (v, w � S^*). Se dice que existe una relación de Thue entre v y w, lo que se representa mediante v �* w, si se verifica que

v = w

o

v �+ w

Consideraremos las propiedades de esta relación..

•       Propiedad reflexiva. Para todo x � S^* se verifica que

x �* x

El cumplimiento de esta propiedad se deriva de la misma definición de la relación. (Siempre se cumplirá que x = x).

•       Propiedad transitiva. Sean tres palabras cualesquiera u, v, w � S^*. Si u �* v, v �* w, entonces u �* w.

Veamos la demostración del cumplimiento de esta propiedad. Partimos de u�* v. Ello significa que :

a) u = v. En este caso, se cumple la propiedad, ya que como v�* w y u = v, entonces

�u �* w

b) u�+ v. En esta caso v puede obtenerse de u mediante una derivación de una longitud determinada (supongamos que sea i). Por otra parte, de v�* w se deduce que

b.1) v = w. En esta caso, la propiedad se cumple, ya que al ser iguales v y w, podré obtener w a partir de u, mediante una derivación de longitud i, y por definición de la relación de Thue se cumplirá que u �* w.

b.2) v �+ w. En este caso, w se puede obtener de u mediante una derivación de una longitud determinada (digamos que sea j). En este caso, al poder obtenerse v a partir de u, resulta que podremos obtener w a partir de u, mediante una derivación de longitud i+j.

Por tanto, en todos los casos posibles se cumple la propiedad transitiva.

•       Propiedad simétrica. Es general esta propiedad no se cumple. Para que una relación de Thue la cumpla se necesita imponer una restricción adicional al conjunto P de producciones : para toda regla x ::= y � P tendría que existir otra de la forma y ::= x � P. Es decir, toda regla tendría que tener su inversa.

Evidentemente, cuando la relación de Thue cumple las tres propiedades anteriores, se trata de una relación de equivalencia. En este caso se representará mediante el símbolo .

•       Cálculo asociativo

Se denomina cálculo asociativo a un alfabeto S, un conjunto de producciones P sobre las palabras de ese alfabeto, y la relación de equivalencia de Thue, basada en P, que asocia a cada palabra otras palabras del mismo alfabeto. Al estar manejando una relación de equivalencia, se definirá una partición del conjunto S^* en clases de equivalencia.

Se denomina palabra irreducible de una clase de equivalencia a una palabra de dicha clase que no puede deducirse (derivarse) de ninguna otra de menor longitud, por la aplicación del las reglas de P.

El problema de decidir si dos palabras cualesquiera, v y w, pertenecen a la misma clase no siempre tiene solución. Pero si se puede establecer que v pertenece a la misma clase que cierta palabra irreducible, y que w está también en relación con dicha palabra irreducible, entonces v y w pertenecen a la misma clase.

Ejemplo : consideremos el alfabeto S = {0 , 1} y el siguiente conjunto de producciones :

P={(00 ::= l), (11 ::= l), (l ::= 00), (l ::= 11)}. Se intenta ver si las palabras 10111100101 y 111000101 pertenecen a la misma clase.

10111100101 101111101 1011101 10101

--- -- --

111000101 1000101 10101

--- ---

Resulta imposible aplicar a la palabra 10101 ninguna de las reglas de P que den lugar a una disminución de longitud. Por tanto, 10101 es una palabra irreducible de la clase. Al estar 10111100101 y 111000101 en relación con la misma palabra irreducible, podemos afirmar que estas palabras se encuentran dentro de la misma clase de equivalencia.

En general este problema será siempre resoluble en el caso en que haya una sola palabra irreducible en cada clase. Esto, sin embargo, no siempre es cierto. Por ejemplo, consideremos el mismo alfabeto que en el ejemplo anterior (S) y sea P el siguiente conjunto de reglas de producción :

P={(000 ::= 00), (010 ::= 00), (101 ::= 11), (111 ::= 11),

(00 ::= 000), (00 ::= 010), (11 ::= 101), (11 ::= 111)}

Consideremos ahora la palabra 01010. Se verifica que

01010 0010 000 00

----- ----- -----

01010 0110

----

01010 0100 000 00

----- ----- -----

y las dos palabras irreducibles, obviamente, pertenecen a la misma clase.

8.- Sistemas formales

Se denomina sistema formal a una cuádrupla de conjuntos

(S , F, A, R)

donde :

S : alfabeto

F : lenguaje sobre S. Es decir F � S^*, y se denomina conjunto de fórmulas.

A : subconjunto de F, A � F, y se llama conjunto de axiomas.

R : es una correspondencia de Fⁿ en F, que se denomina conjunto de reglas de deducción. Los elementos de Fⁿ se llaman hipótesis o premisas.

Las reglas de deducción permiten obtener elementos de F a partir de elementos de A y otros elementos de F obtenidos como pasos intermedios.

A tener en cuenta que las palabras a obtener han de pertenecer a F. Para ello se parte de los axiomas. Sobre estos axiomas se aplican reglas de R.

Si A = f el sistema formal se denomina sistema de Markov.

•       Sistemas combinatorios

Son sistemas formales, con las siguientes particularidades : F = S^*, c(A) = 1, y R es una correspondencia de F en F.

Sea (a, b) � R. Entonces xay � ubv es una ley particular asociada al esquema de leyes (a, b) por intermedio de x, y, u, v. Estas leyes particulares pueden clasificarse de la siguiente manera :

•       Si x = u, y = v, la ley se llama semi-thueica : xay � xby

•       Si x = v = l, e y = u, la ley se llama normal : ay � yb

•       Si y = u = l, e x = v, la ley se llama antinormal : xa � bx

Se llama ley inversa de una dada xay � ubv a la ley ubv � xay. Para que esta ley pertenezca al sistema combinatorio es necesario que la regla (b, a) pertenezca a R.

Los sistemas combinatorios pueden pertenecer a alguno de los grupos siguientes (entre otros) :

•       Si todas las leyes que se pueden formar con las reglas son semi-thueicas, el sistema combinatorio se denomina semi-thueico.

•       Sistema combinatorio thueico, si cada regla lleva asociada su inversa.

•       Sistema de Post, si sólo contiene leyes normales y sus inversas (que serán antinormales).

•       Teoremas

Sea el sistema combinatorio (S , F, A, R) y la sucesión x₁, x₂, ..... x_n, donde x₁ � A (es decir, es un axioma) y x_i � x_i+1 una ley particular asociada a alguna de las reglas de R. Se dice entonces que x_n es un teorema del sistema combinatorio y la sucesión presentada su deducción.

Ejemplo : Sea el sistema combinatorio

({0, 1, S}, {0, 1, S}*, {S}, {(S, 01), (S, 0S1)})

y sea la sucesión S, 0S1, 00S11, 000111. Resulta evidente que

S � 0S1 � 00S11 � 000111

son leyes particulares asociadas a las reglas de R. Por lo tanto, 000111 es un teorema del sistema combinatorio. Además, sobre este teorema no puede aplicarse ya ninguna regla.

Las deducciones de los teoremas pueden representarse en forma de árbol. La siguiente figura muestra la deducción del teorema anterior :

Si un teorema tiene dos demostraciones diferentes, se trata de un teorema ambiguo. Por ejemplo, en el siguiente esquema combinatorio

({0, 1, S}, {0, 1, S}*, {S}, {(S, 0S), (S, S1), (S,0), (S,1)})

el teorema 01 es ambiguo, ya que existen para él dos demostraciones diferentes

S � 0S � 01

S � S1 � 01

- TEMA 3 -

GRAMÁTICAS FORMALES 

1.- Concepto básico de gramática

Una gramática define la estructura de las frases y de las palabras de un lenguaje. Aplicada a los lenguajes naturales se trata de una disciplina muy antigua, ya que los primeros trabajos aparecieron en la India durante la primera mitad del primer milenio antes de Cristo, alcanzando un alto nivel de desarrollo con Panini, que se supone vivió entre los siglos VII y IV antes de Cristo, y que desarrolló la gramática sánscrita hasta límites inusitados.

También surgió una corriente de investigación gramatical en Grecia, cuyo representante máximo es el sofista Protágoras (485-411 antes de Cristo).

Ejemplo en lengua castellana.

La gramática de la lengua castellana se expresa mediante reglas sencillas que definen las partes de la oración, y que permiten comprobar fácilmente si una frase determinada es o no correcta. Como ejemplo de aplicación se analizará la frase "el estudiante daba apuntes a Juan en el bar".

La primera regla que aplicaremos dice así : "UNA ORACIóN CONSTA DE SUJETO Y PREDICADO".

En nuestro caso, el sujeto será "el estudiante", y el predicado el resto de la oración.

Esta regla se cumple, pero todavía, cada una de las partes que constituyen la frase (sujeto y predicado) son demasiado complicadas. Por tanto hemos de aplicar nuevas reglas, como la siguiente : "UN SUJETO ES UNA FRASE NOMINAL".

Vemos que esta regla, por sí misma, no nos dice nada. Se hace necesaria la definición de frase nominal, en cuanto a sus elementos constituyentes, para que se pueda progresar en el análisis de la frase.

La definición de frase nominal viene dada por la regla : "UNA FRASE NOMINAL CONSTA DE UN GRUPO NOMINAL Y DE UN CALIFICATIVO, QUE PUEDE FALTAR".

En nuestro caso, el grupo nominal es "el estudiante", mientras que el calificativo no aparece. Al estar contemplado este caso en la regla de la gramática, la estructura de nuestra frase se ajusta a la gramática.

A su vez, el grupo nominal puede descomponerse aún más : a saber "UN GRUPO NOMINAL CONSTA DE UN ARTíCULO, QUE PUEDE FALTAR, Y DE UN NOMBRE". En el grupo nominal de nuestra frase, el artículo será "el" y el nombre "estudiante".

Pasemos ahora a estudiar el predicado. Necesitamos una nueva regla que nos indique la forma en que se compone, para poder comprobar su validez. Esta regla, en castellano, es la siguiente : "UN PREDICADO CONSTA DE UN VERBO SEGUIDO DE UN CONJUNTO DE COMPLEMENTOS".

En nuestro predicado, el verbo es "daba" y el conjunto de complementos viene constituido por "apuntes a Juan en el bar".

La siguiente regla nos permite verificar la validez del conjunto de complementos : "UN CONJUNTO DE COMPLEMENTOS CONSTA DE UN COMPLEMENTO DIRECTO, QUE PUEDE FALTAR, UN COMPLEMENTO INDIRECTO, QUE PUEDE FALTAR, Y CERO, UNO O VARIOS COMPLEMENTOS CIRCUNSTANCIALES".

En nuestro caso, "apuntes" será el complemento directo, "a Juan" el indirecto y "en el bar" es un complemento circunstancial.

Para determinar la estructura del complemento directo, tenemos la regla "UN COMPLEMENTO DIRECTO ES UNA FRASE NOMINAL".

Ya se vio lo que era una frase nominal. Vemos aquí por qué se introduce una regla del tipo "UN SUJETO ES UNA FRASE NOMINAL" o "UN COMPLEMENTO DIRECTO ES UNA FRASE NOMINAL", que necesita la introducción de otra regla que defina la estructura de la frase nominal. Esto se hace así para poder usar la definición de "frase nominal" en distintas reglas, que remitan, en última instancia, a la definición de "frase nominal". Si la "frase nominal" no se utilizase más que en una regla, bastaría con definir allí su estructura y no generaría la aparición de una regla aparte.

La descripción del complemento indirecto viene dada por "UN COMPLEMENTO INDIRECTO ES LA PREPOSICIóN a SEGUIDA DE UNA FRASE NOMINAL".

Para concluir con la comprobación sobre nuestra frase, ya sólo se necesita una regla para definir los complementos circunstanciales. "UN COMPLEMENTO CIRCUNSTANCIAL ES UNA PREPOSICIóN SEGUIDA DE UNA FRASE NOMINAL".

Siguiendo la aplicación de todas estas reglas, se puede descomponer la frase en sus componentes elementales, comprobando así mismo que la estructura de nuestra frase cumple las reglas mostradas.

La notación de reglas de producción vista anteriormente resulta muy útil para representar las reglas de una gramática. Las reglas anteriores, expresadas de esta forma quedarían :

<oración> ::= <sujeto><predicado>

<sujeto> ::= <frase_nominal>

<frase_nominal> ::= <grupo_nominal>

<frase_nominal> ::= <grupo_nominal><calificativos>

<grupo_nominal> ::= <nombre>

<grupo_nominal> ::= <artículo><nombre>

<calificativo> ::= <conjunción><oración>

<calificativo> ::= <adjetivo>

<predicado> ::= <verbo><complementos>

<complementos> ::= <directo><indirecto><circunstancial>

<complementos> ::= <directo>< circunstancial>

<complementos> ::= <indirecto><circunstancial>

<complementos> ::= <circunstancial>

<circunstancial> ::= l

<circunstancial> ::= <circunstancial><circunstancial>

<directo> ::= <frase_nominal>

<indirecto> ::= "a"<frase_nominal"

<circunstancial> ::= <preposición><frase_nominal>

Obsérvese la existencia de recursividad en las reglas de producción. Algunas la introducen directamente, como en el caso <circunstancial> ::= <circunstancial><circunstancial>, mientras que en otras de forma indirecta (<oración> <sujeto> <frase_nominal> <calificativo> <oración>).

Para completar las reglas sintácticas anteriores se necesita información morfológica sobre las palabras. Esta información también puede escribirse en forma de reglas de producción :

<nombre> ::= "estudiante"

<nombre> ::= "Juan"

<nombre> ::= "apuntes"

<nombre> ::= "bar"

<artículo> ::= "el"

<verbo> ::= "daba"

<preposición> ::= "en"

Teniendo en cuenta todas estas reglas, y aplicando el concepto de derivación definido anteriormente, se puede obtener la frase considerada partiendo de una palabra de una sola letra <oración>. Este símbolo es uno de los que componen el alfabeto considerado.

Veamos cómo :

<oración> � <sujeto><predicado> � <frase_nominal><predicado> � <grupo_nominal><predicado> � <artículo><nombre><predicado> � el <nombre><predicado> � el estudiante <predicado> �

el estudiante <verbo><complementos> �

el estudiante daba <complementos> �

el estudiante daba <directo><indirecto><circunstancial> �

el estudiante daba apuntes <indirecto><circusntancial> �

el estudiante daba apuntes a <frase_nominal><circunstancial> �

el estudiante daba apuntes a <grupo_nominal><circunstancial> �

el estudiante daba apuntes a <nombre><circusntancial> �

el estudiante daba apuntes a Juan <circunstancial> �

el estudiante daba apuntes a Juan <preposición><frase_nominal> �

el estudiante daba apuntes a Juan en <frase_nominal> �

el estudiante daba apuntes a Juan en <grupo_nominal> �

el estudiante daba apuntes a Juan en <articulo><nombre> �

el estudiante daba apuntes a Juan en el <nombre> �

el estudiante daba apuntes a Juan en el bar

Por tanto, al haber una derivación que produce dicha frase partiendo de <oración>, se sigue que se trata de una frase correcta que pertenece al lenguaje representado por la gramática.

Consideremos ahora un ejemplo de gramática, en un lenguaje artificial. Consideremos la instrucción de cualquier lenguaje

x = y+2*z

Intentemos generarla a partir del símbolo <instrucción>, mediante el siguiente conjunto de producciones :

<instrucción> ::= <asignación>

<asignación> ::= <identificador>"="<expresión>

<expresión> ::= <sumando>

<expresión> ::= <sumando>"+"<expresión>

<sumando> ::= <factor>

<sumando> ::= <factor> "*" <sumando>

<factor> ::= <identificador>

<factor> ::= <número>

al que se añaden las reglas morfológicas :

<identificador> ::= "x"

<identificador> ::= "y"

<identificador> ::= "z"

<número> ::= "2"

Veamos la forma en que se obtendría la expresión x = y+2*z a partir de <instrucción> :

<instrucción> � <asignación> � <identificador> = <expresión> � x = <expresión> � x = <sumando> + <expresión> �

x = <factor> + <expresión> �

x = <identificador> + <expresión> �

x = y+ <expresión> �x = y+ <sumando> �

x = y+ <factor> * <sumando> �

x = y+ <número> * <sumando> �

x = y+2* <sumando> � x = y+2* <factor> �

x = y+2* <identificador> � x = y+2*z

2.- Concepto formal de gramática

Se llama gramática formal a la cuádrupla

G = (S_T,S_N, S, P)

donde

S_T, alfabeto de símbolos terminales

S_N, alfabeto de símbolos no terminales

S � S_N, es el axioma, símbolo inicial o símbolo distinguido

P es un conjunto finito de reglas de producción de la forma u ::= v, donde u � S^* y v � S^*.

Se verifica además que S_T � S_N = f y el alfabeto sobre el que trabajaremos será S = S_T É S_N

Ejemplo : consideremos la gramática definida por

S_T = {0, 1, 2 ,3 ,4 ,5 ,6 ,7 8, 9, 0}

S_N = {N, C}

S = N

P = { N::=NC, N::=C, C::=0, C::=1, C::=2, C::=3, C::=4, C::=5, C::=6, C::=7, C::=8, C::=9}

Es posible establecer una notación simplificada para las reglas de producción. Si existen dos reglas de la forma

u::=v

u::=w

se pueden representar de la forma :

u::=v | w

Esta forma de representar las reglas de producción recibe el nombre de "forma normal de Backus" (o BNF).

•       Formas sentenciales y sentencias

Sea una gramática G = (S_T,S_N, S, P). Una palabra x � S^* se denomina forma sentencial de G si se verifica que

S �* x

es decir, existe una relación de Thue entre el axioma de la gramática y la palabra.

Considerando la gramática anterior, las siguientes son formas sentenciales : NCC, NC2, 123.

S = N � NC � NCC

S = N � NC � NCC � NC2

S = N � NC � NCC � CCC � 1CC � 12C � 123

Si una forma sentencial x cumple que x � S_T^*, se dice que x es una sentencia o instrucción de G. Es decir, las sentencias estarán compuestas únicamente por símbolos terminales.

•       Lenguaje asociado a una gramática

Sea una gramática G = (S_T,S_N, S, P). Se llama lenguaje asociado a la G, o lenguaje generado por G, o lenguaje descrito por G, al conjunto :

L(G) = { x | S �* x & x � S_T^* }

Es decir, será el conjunto de todas las sentencias de la gramática.

Ya que la teoría de gramáticas formales (ideada por Chomsky), junto con la notación de Backus, nos proporciona una forma de describir lenguajes, esta simbología debe considerarse como un metalenguaje (es decir, un lenguaje que sirve para describir lenguajes).

•       Frases y asideros

Sea G una gramática y v = xuy una de sus formas sentenciales. Se dice que u es una frase de la forma sentencial v, respecto del símbolo no terminal U, si

S �* xUy

U �+u

Resulta obvio considerar que si U es una forma sentencial, entonces todas las frases que derivan de U serán, a su vez, formas sentenciales de G.

Se dice que u es una frase simple de la forma sentencial v = xuy, respecto del símbolo no terminal U, si

S �* xUy

U �u

Se denomina asidero de una forma sentencial v a la frase simple situada más a su izquierda.

•       Recursividad

Una gramática G se llama recursiva en U, U � S_N, si

U �+xUy

Si x es la palabra vacía, se dice que la gramática es recursiva a izquierdas. Si y es la palabra vacía, se dice que la gramática es recursiva a derechas.

De igual forma, se dice que una producción es recursiva si

U::= xUy

Se dice que la producción es recursiva a izquierdas si x =l. Será recursiva a derechas si

y =l.

Si un lenguaje es infinito, la gramática que lo representa ha de ser recursiva.

3.- Tipos de gramáticas

Chomsky clasificó las gramáticas en cuatro grandes grupos : G0, G1, G y G3. Cada uno de estos grupos incluye las gramáticas del siguiente, de acuerdo con el siguiente esquema :

G3 � G2 � G1 � G0

•       Gramáticas tipo 0

Las reglas de producción tienen la forma u ::= v, donde

u � S⁺

v � S^*

u = xZy con x � S^*, y � S^*

Z � S_N

sin imponer ninguna otra restricción adicional.

Algunas palabras sobre la forma de las reglas de producción. Observar que la parte izquierda no puede ser la palabra vacía. Además, en la parte izquierda (u) ha de aparecer algún símbolo que no sea terminal. Recordar que las reglas de producción no podrán aplicarse sobre símbolos terminales, es decir, la presencia de cadenas compuestas únicamente por símbolos terminales significa la imposibilidad de volver a aplicar reglas de producción sobre ella.

Los lenguajes representados por estas gramáticas reciben el nombre de lenguajes sin restricciones. Puede demostrarse que todo lenguaje representado por este tipo de gramáticas pueden ser descritos también por una grupo de gramáticas un poco más restringido (llamado de gramáticas de estructura de frases), cuyas producciones tienen la forma xZy ::= xvy, donde x, y, v � S^*, siendo Z un símbolo no terminal.. Ya que v puede ser la palabra vacía, se sigue que en estas reglas podemos encontrar situaciones en que la parte derecha sea más corta que la izquierda. Las reglas en que ocurre esto se denominan compresoras. Una gramática que contenga al menos una regla compresora se denomina gramática compresora.

En las gramáticas compresoras, las derivaciones pueden ser decrecientes, ya que la longitud de las palabras puede disminuir en cada uno de los pasos de derivación.

Ejemplo : sea la gramática G = ({a, b}, {A, B, C}, A, P), donde P es igual a

A ::= aABC | abC

CB ::= BC

bB ::= bb

bC ::= b

Esta gramática es de tipo 0, pero no es de estructura de frases, debido a la presencia de la regla CB ::= BC.

Estudiaremos la estructura de esta regla. Veamos todas las formas de considerarla, de acuerdo a la definición anterior (xZy ::= xvy, con x, y, v � S^*, siendo Z un símbolo no terminal)

a) Vamos a considerar x = l, Z = C, y = B. Así tendríamos formada la parte izquierda de la producción, pero para la derecha tendríamos

vB

y sea cual sea v, no podrá ser BC

b) Vamos a considerar x = C, Z = B, y = l. Así tendríamos formada la parte izquierda de la regla, pero en la derecha tendríamos

Cv, y sea v lo que sea no podremos obtener CB.

Ya no es posible hacer ninguna otra descomposición, por lo que esta regla no pertenece al esquema de reglas visto para las gramáticas de estructura de frases.

Estudiemos otra regla de producción : A ::= aABC. Para ello procederemos de la misma manera :

Con respecto a esta regla, no hay duda alguna. Z = A, x= l, y =l. Si hacemos v = aABC, vemos que la regla se ajusta al formato considerado.

Sin embargo la regla CB ::= BC puede descomponerse en las cuatro reglas siguientes, que permiten obtener las mismas derivaciones con más pasos, pero ajustándose a las condiciones exigidas para que la gramática sea de estructura de frases.

CB ::= XB

XB ::= XY

XY ::= BY

BY ::= BC

La gramática resultante, de esta manera, tendrá 3 reglas de producción más y dos símbolos adicionales (X, Y) en el alfabeto de símbolos no terminales.

Veamos la derivación de la sentencia aaabbb, mediante la gramática original :

A � a(A)BC � aa(A)BCBC � aaab(CB)CBC � aaa(bB)CCBC � aaab(bC)CBC � aaab(bC)BC � aaab(bB)C � aaabb(bC) � aaabbb

Se observa también que la gramática es compresora, debido a la presencia de la regla bC ::= b.

Puede comprobarse que el lenguaje generado por esta gramática es { aⁿbⁿ | n = 1, 2, ....}.

•       Gramáticas tipo 1

Las reglas de producción de esta gramática tienen la forma

xAy ::= xvy

donde x, y � S^*, v � S⁺ y A ha de ser un símbolo no terminal.

Ya que v no puede ser la palabra vacía, se deduce de aquí que este tipo de gramáticas no pueden tener reglas compresoras. Se admite una excepción en la regla S ::= l (siendo S el axioma de la gramática). Como consecuencia se tiene que la palabra vacía pertenece al lenguaje generado por la gramática sólo si contiene esta regla.

Los lenguajes generados por este tipo de gramáticas se denominan "dependientes del contexto". La forma particular de las reglas (xAy ::= xvy ) puede entenderse de la siguiente manera : A puede transformarse en v sólo si aparece en el contexto definido por x e y.

Evidentemente todas las gramáticas de tipo 1 son también de tipo 0, y así, todos los lenguajes dependientes de contexto serán también lenguajes sin restricciones.

Ejemplo : G = ({S, B, C}, {a, b, b}, S,P),

donde P está compuesto por las siguientes reglas

S := aSBc | aBC

bB := bb

bC ::= bc

CB ::= BC

cC ::= cc

aB ::= ab

•       Gramáticas tipo 2

Las reglas de estas gramáticas se ajustan al siguiente esquema

A ::= v

donde v � S^*, y A ha de ser un símbolo no terminal. En concreto v puede ser l.

Para toda gramática de tipo 2 existe una gramática equivalente desprovista de reglas de la forma A ::= l, que generará el mismo lenguaje que la de partida, excepto la palabra vacía. Si se le añade a la segunda gramática la regla S ::= l, las gramáticas generarán el mismo lenguaje. Por lo tanto, se pueden definir las gramáticas de tipo 2 de una forma más restringida, en el que las reglas de producción tendrán la siguiente forma

A ::= v

donde v � S⁺, y A ha de ser un símbolo no terminal. Además podrán contener reglas de la forma S ::= l.

Los lenguajes generados por este tipo de gramáticas se denominan independientes de contexto, ya que la conversión de A en v puede realizarse independientemente del contexto en que aparezca A.

La mayor parte de los lenguajes de programación de ordenadores pueden describirse mediante gramáticas de este tipo.

Ejemplo : sea la gramática G = ({a, b}, {S}, S, { S ::= aSb | ab}).

Se trata de una gramática de tipo 2. Veremos la derivación de la palabra aaabbb :

S � aSb � aaSbb � aaabbb

Puede verse que el lenguaje definido por esta gramática es

{aⁿbⁿ | n=1, 2, ...}

Hay que considerar que un mismo lenguaje puede generarse por muchas gramáticas diferentes. Sin embargo, una gramática determinada describe siempre un lenguaje único.

•       Gramáticas tipo 3

Estas gramáticas se clasifican en los dos grupos siguientes :

a) Gramáticas lineales por la izquierda, cuyas reglas de producción pueden tener una de las formas siguientes :

A ::= a

A ::= Va

S ::= l

donde a � S_T, A, V � S_N, y S es el axioma de la gramática.

b) Gramáticas lineales por la derecha, cuyas reglas de producción tendrán la forma :

A ::= a

A ::= aV

S ::= l

donde a � S_T, A, V � S_N, y S es el axioma de la gramática.

Los lenguajes representados por este tipo de gramáticas se denominan lenguajes regulares.

Ejemplo : G1 = ({ 0, 1}, {A, B}, A, { A ::= B1 | 1, B ::= A0})

Se trata de una gramática lineal por la izquierda que describe el lenguaje L1 = { 1, 101, 10101, ... } = {1(01)ⁿ | n = 0, 1, 2, ...}

G2 = ({ 0, 1}, {A, B}, A, { A ::= 1B | 1, B ::= 0A})

Se trata de una gramática lineal derecha que genera el mismo lenguaje que la gramática anterior.

4.- Equivalencia de gramáticas

Se dice que dos gramáticas son equivalentes cuando describen el mismo lenguaje.

•       LEMA

Para toda gramática lineal derecha existe otra gramática lineal izquierda equivalente, que no contiene reglas de la forma A ::= aS, donde a � S_T, A � S_N, y S es el axioma de la gramática.

Demostración :

Si la gramática no contiene reglas de la forma A ::= aS, ya está demostrado. Si las contiene, se introduce un nuevo símbolo no terminal. A continuación, para cada regla de la forma

S ::= x ( x � S⁺), se añadirá una nueva regla de la forma B ::= x, donde B es el nuevo símbolo no terminal incluido en el conjunto de símbolos no terminales. Finalmente todas las reglas de la forma A ::= aS se transforman en A ::= aB. Por construcción, resulta evidente que la nueva gramática genera el mismo lenguaje que la gramática de partida, careciendo de reglas del tipo A ::= aS.

Ejemplo : sea G1 = ({a, b}, {S, A}, S, { S ::= bA, A ::= aS | a }), que describe el lenguaje L = { ba, baba, bababa, ....}. Aplicando el método anterior se obtendrá la gramática equivalente, sin reglas de la forma A ::= aS.

La nueva gramática, equivalente a la anterior, será :

G2 = ({a, b}, {S, A, B}, S, { S::= bA, A ::= aB | a, B ::= bA }), que describe el mismo lenguaje que G1.

•       TEOREMA

Para toda gramática lineal derecha existe otra gramática lineal izquierda equivalente

Demostración :

Sea la gramática lineal derecha G1. De acuerdo al lema anterior, se puede obtener a partir de ella otra gramática G2, equivalente a G1 y sin reglas de la forma A ::= aS.

A partir de las reglas de esta gramática (G2), se construye el siguiente grafo :

a) El grafo tendrá tantos nodos como símbolos haya en S_N más uno. Cada uno de los nodos estará etiquetado como uno de los símbolos de S_N. El nodo adicional tendrá la etiqueta l.

b) Cada regla de la forma A ::=aB se representa como un arco dirigido de A a B, etiquetado con a.

c) Cada regla de la forma A ::= a se representa como un arco dirigido de A a l, etiquetado con a.

d) La regla S ::= l, si existe, se traduce como una rama sin etiqueta desde S hasta l.

Por construcción, cualquier palabra del lenguaje definido por G2 define un camino en el grafo anterior, desde el nodo S hasta l, y sus letras corresponden a las etiquetas de los arcos recorridos.

Se pasa ahora de este grafo a otro, construido de la siguiente forma :

a) Se intercambian las etiquetas de los nodos S y l.

b) Se invierte la dirección de todas las ramas.

Este grafo puede considerarse como la representación de una gramática lineal izquierda G3, con los mismos alfabetos terminal y no terminal que G2, el mismo axioma y cuyo conjunto de reglas se obtiene así :

a) Cada rama dirigida de A a B, con la etiqueta a, corresponde a una regla de la forma A ::=Ba.

b) Cada rama dirigida desde el nodo A hasta el nodo l, con la etiqueta a, corresponde a una regla de la forma A ::= a.

c) La rama sin etiqueta dirigida desde S hasta l, si existe, se corresponde con la regla S ::= l.

Por construcción, G1, G2 y G3 describen el mismo lenguaje y por tanto, son equivalentes.

Ejemplo : consideremos la gramática lineal derecha del ejemplo anterior G1 = ({a, b}, {S, A}, S, { S ::= bA, A ::= aS | a }), que describe el lenguaje L = { ba, baba, bababa, ....}.

Para obtener la gramática lineal izquierda equivalente, hemos de eliminar las reglas de la forma A ::= aS. Siguiendo el procedimiento indicado en el lema anterior, y según se veía en el ejemplo, se obtiene la gramática equivalente a la anterior :

G2 = ({a, b}, {S, A, B}, S, { S::= bA, A ::= aB | a, B ::= bA }),

que describe el mismo lenguaje que G1.

A partir de ella se construye el siguiente grafo :

Invirtiendo la dirección de los arcos e intercambiando las etiquetas de los nodos S y l, obtendremos el siguiente grafo :

Interpretando el grafo de la manera explicada en la demostración del teorema, obtendríamos el siguiente conjunto de reglas

S ::= 1 | A1

A ::= B0

B ::= A1 | 1

que corresponderían al conjunto de reglas de G3 (gramática lineal izquierda equivalente a G1). El resto de elementos de G3 serían idénticos a los de G2 (es decir, el mismo conjunto de símbolos terminales y no terminales, y siendo el axioma también S).

•       Árboles de derivación

A toda derivación de una gramática de tipo 1, 2 ó 3 le corresponde un árbol de derivación. Este árbol se construye así :

a) La raíz del árbol corresponde al axioma de la gramática

b) Una derivación directa se representa por un conjunto de ramas que salen de un nodo determinado. Al aplicar una regla, uno de los símbolos de la parte izquierda de la producción queda sustituido por la palabra de la parte derecha. Por cada uno de los símbolos de x se dibuja una rama, que parte del nodo correspondiente al símbolo sustituido.

En cada rama, el nodo de partida se denomina padre. El final se denomina hijo del primero. Dos nodos hijos del mismo padre se denominan hermanos. Un nodo es ascendiente de otro si es su padre o ascendiente de su padre. Un nodo es descendiente de otro si es su hijo o es descendiente de su hijo.

A lo largo del proceso de construcción del árbol, los nodos finales de cada paso, leídos de izquierda a derecha, forman la forma sentencial obtenida por la derivación representada por el árbol.

Será rama terminal aquella dirigida hacia un símbolo terminal. Este nodo se llama hoja. El conjunto de hojas, leído de izquierda a derecha, forma la sentencia generada por la derivación.

Ejemplo : sea la gramática G = ({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0}, {N. C}, N, {N  ::= C | NC, C ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 }).

Consideraremos la derivación : N � NC � NCC � CCC � 2CC � 23C � 235

El árbol de derivación correspondiente sería :

•       Subárbol

Dado un árbol correspondiente a una derivación, se denomina subárbol al árbol cuya raíz es un nodo cualquiera y cuyos nodos son los descendientes de éste.

Teorema : Los nodos terminales de un subárbol, leídos de izquierda a derecha, forman una frase respecto de la raíz del subárbol.

Demostración : Sea U la raíz del subárbol, y sea u la palabra formada por los nodos terminales del subárbol. Así, se verifica que

U �+u

Sea x la palabra formada, leyendo de izquierda a derecha, los nodos terminales del árbol situados a la izquierda de los del subárbol. Sea y la palabra formada, leyendo de izquierda a derecha, los nodos terminales situados a la derecha de los del subárbol. De esta forma se verifica que xuy es la sentencia definida por el árbol completo.

Como S �*xUy y además U �+u, se sigue que u es una frase respecto de U y de la forma sentencial xuy.

Si todos los nodos terminales del subárbol son hijos de la raíz, entonces u es una frase simple.

•       Proceso inverso

Para cada derivación existe un único árbol de derivación. Sin embargo, de una misma sentencia pueden obtenerse, a veces, varias derivaciones diferentes.

Por ejemplo, el mismo árbol anterior puede aplicarse a las siguientes derivaciones :

N � NC � NCC � CCC � 2CC � 23C � 235

N � NC � NCC � CCC � C3C � 23C � 235

N � NC � NCC � CCC � 2CC � 2C5 � 235

•       Ambigüedad

Como se vio en el ejemplo anterior, una misma sentencia puede obtenerse como resultado de varias derivaciones diferentes, pero a las que les corresponde un único árbol de derivación.

Pero hay otros casos en que para una misma sentencia podemos tener varios árboles de derivación diferentes. En este caso, se dice que la sentencia es ambigua.

Ejemplo : G = ({i, +, *, (, )}, {E}, E, E ::= E + E | E * E | ( E ) | i })

Consideremos la sentencia : i+i*i. Para esta sentencia podemos tener los siguientes árboles de derivación :

Esto no quiere decir que el lenguaje sea ambiguo, ya que se puede encontrara una gramática equivalente a la anterior, sin ser ambigua. Sin embargo, hay lenguajes para los cuales es imposible encontrar gramáticas no ambiguas. Estos lenguajes se denominan "inherentemente ambiguos".

Por ejemplo, se puede ver que la siguiente gramáticas es equivalente a la anterior sin ser ambigua :

G = ({i, +, *, (, )}, {E, T, F}, E, E ::= T | E + E, T ::= F | T * F, F = ( E ) | i })

En esta gramática existe un sólo árbol de derivación para la sentencia i+i*i.

- TEMA 4-

SISTEMAS, MODELOS Y VISTAS

1.- Introducción

Paralelamente al desarrollo de la informática se produce una preocupación por establecer métodos y técnicas que permitan que el proceso de desarrollo software sea más rentable : menos tiempo de desarrollo, menos personas involucradas, menor coste de mantenimiento, etc.

Dentro de los intentos por conseguir estas mejoras se pueden citar : programación estructurada, herramientas CASE, etc. En esta dinámica aparecen también las tecnologías de orientación a objetos.

El objetivo fundamental en el caso de la orientación a objetos es la reutilización.

A la orientación a objetos se aporta la experiencia de un gran número de proyectos desarrollados con Smalltalk. Algunas de las conclusiones obtenidas son :

n  el proceso de desarrollo software conlleva, al menos, tanto de aprendizaje como de creación.

n  lo interesante es construir sistemas a partir de pocos y amplios conceptos.

n  las estructuras y relaciones son mucho más importantes que los algoritmos y las funciones.

n  la pretensión es no comenzar el desarrollo a partir de cero.

La verdadera potencia de las tecnologías de orientación a objetos no se pone de manifiesto a través de la utilización de ningún lenguaje de programación en particular, si no mediante la modelización.

2.- Modelización

El objetivo fundamental de las técnicas que veremos es la construcción de modelos.

Esto es así porque la orientación a objetos se basa en la noción de que los objetos identificados en un problema, en la fase de análisis, ocupan un lugar significativo en la solución.

Como primera aproximación indicar que los métodos de orientación a objetos se centran en una visión estructural de los problemas, frente a la visión funcional propuesta por otro tipo de tecnologías.

La diferencia entre la visión estructural y funcional de un problema puede ponerse de manifiesto a través del siguiente ejemplo. Supongamos que en una ciudad que no conocemos queremos ir de un punto A a otro B. Según la visión estructural la propuesta sería conseguir un mapa de la ciudad. Frente a ella la visión funcional optaría por preguntar a cualquier persona que pasara por la calle. Examinemos las diferencias entre las dos soluciones. Sin duda alguna lo más rápido es preguntar por la calle, pero en este caso dependemos de la claridad de las explicaciones que nos den y de la capacidad que tengamos de no perder ninguna de las marcas esenciales para la identificación del camino. Sin embargo con un mapa comprenderemos la estructura del terreno en que nos movemos, al ser un modelo basado en entidades reales. La información que se necesita para el desplazamiento aparece reflejada en el mapa.

Además las indicaciones recibidas nos sirven exclusivamente para el desplazamientos entre los puntos A y B. Con el mapa se dispone de información suficiente para realizar movimientos entre dos puntos cualesquiera, siempre que aparezcan en el mapa. Reseñar aquí que mientras que la persona que nos da la información puntual para un desplazamiento es consciente de la función de su respuesta, el cartógrafo que hace el mapa no está interesado, en absoluto, en el tipo de respuestas que buscarán sus usuarios.

Otra ventaja adicional de los mapas (visión estructural) es que resultan mas estables que las indicaciones puntuales (visión funcional). Si se quiere utilizar la indicación algún tiempo después de recibirla quizás no sea útil porque se haya modificado algunas de las marcas vitales (una fuente, un edificio en concreto, etc.). El mapa, sin embargo, seguirá siendo útil siempre que no se produzcan cambios estructurales.

Una nota de precaución sobre la visión estructural. Resulta muy importante considerar la información a reflejar. Así, por ejemplo, el cartógrafo de un mapa de ciudad no incluirá datos geológicos del terreno. Si lo hiciera el mapa podría resultar incluso confuso. En el mismo orden de cosas no tiene sentido abordar la construcción de una visión estructural completa de una gran empresa, por ejemplo, ya que posiblemente quede desactualizado antes de su finalización. Frente a este tipo de situaciones la solución es construir modelos parciales bajo la supervisión de los expertos en cada una de las actividades. La integración de estos modelos parciales nos conduce a la visión global del problema.

3.- Relación entre sistemas y mundo real

El paradigma básico de la tecnología de orientación a objetos radica en considerar que los objetos identificados en un problema, durante la fase de análisis, juegan un papel primordial en la solución, diseño.

Aunque una primera aproximación simplista puede llegar a considerar que la progresión desde un modelo inicial hasta el sistema final es lineal, esto no es así. Esta aproximación se basa en dos principios cuestionables :

n  los conceptos inherentes a la programación orientada a objetos son apropiados para construir modelos abstractos de la realidad

n  no hay diferencias esenciales entre los modelos del mundo real y los modelos de los sistemas software

Esta aproximación está viciada por las siguientes razones :

n  los modelos de la realidad son completamente distintos a los modelos de los sistemas. El mundo no se compone de objetos intercambiando mensajes entre sí. Esto, sin embargo, puede ser un buen punto de partida para la construcción de un sistema

n  mientras que el comportamiento del software es completamente predecible no ocurre lo mismo con el mundo real. Como mucho, se pueden establecer relaciones entre hechos conocidos por ejemplo se puede predecir que el sol no volverá a salir hasta que no se haya ocultado

n  mientras que en la realidad existe concurrencia en los sistemas software no

Como conclusión de estas diferencias habrá que utilizar herramientas y conceptos distintos para construir cada uno de los tipos de modelos considerados (el del mundo y el de los sistemas).

Para modelizar el mundo se usarán dos conceptos fundamentales : objetos y eventos.

Los objetos representarán cosas presentes en la visión del mundo que nos interesa. Pueden ser reales o imaginarias, concretas o abstractas, transitorias o permanentes. En un video-juego todos los objetos presentes serán imaginarios. Un objeto puede ser una función exponencial (sin realidad propia, a menos que consideremos que los objetos matemáticos la poseen). Un matiz importante consiste en considerar que los objetos modelan tipos de objetos más que objetos concretos.

Los eventos representan ocurrencias de cambios de estado en los objetos. Ha de considerarse también que existirán relaciones entre eventos, ya que la ocurrencia de determinados cambios en algunos objetos puede desencadenar cambios en otros.

Según lo comentado hasta ahora en relación a los modelos de la realidad, para su construcción tendremos que identificar los objetos involucrados en la situación considerada, así como los posibles cambios que se pueden producir en sus estados y las relaciones existentes entre unos cambios y otros.

Para la modelización del software se usan los conceptos de objetos y mensajes.

En este tipo de modelos los objetos hacen referencia a encapsulaciones de datos y operaciones asociadas. Es decir, sería el concepto clásico de objeto en la programación orientada a objetos.

Los mensajes se refieren a invocaciones sobre las operaciones asociadas a los objetos.

Consideremos las relaciones entre la situación bajo consideración y estos dos tipos de modelos. Dentro del ámbito software aparece el modelo conceptual. Es un modelo software que imita el comportamiento del mundo, de la situación considerada. Para que el sistema funcione correctamente, este modelo ha de estar en sintonía con la situación real. Es decir, ha de reflejar todos los cambios ocurridos ante los que el sistema software ha de reaccionar.

La forma en que el sistema se comunica con el exterior puede ser :

n  directa : a través de sensores y transductores. Estos dispositivos detectan cambios y los comunican al sistema

n  indirecta : detectadas por algún operador humano, que lo comunica al sistema mediante alguna interfaz de usuario

Los sistemas influyen en el mundo de forma análoga a lo comentado anteriormente : de forma directa y de forma indirecta.

Un esquema en el que se matizan estas relaciones aparece a continuación :

Observaciones sobre el esquema :

n  aquí se considera al mundo como algo totalmente separado al sistema software. En determinadas circunstancias esto no es así. Podemos imaginar, por ejemplo, las consecuencias que un fallo en un sistema de un banco puede tener sobre su funcionamiento. En este caso la mediación no es ni a través de sensores ni mediante operadores humanos

n  en el gráfico se distingue entre aquellas personas cuya única misión es actuar sobre el sistema y las que componen el resto del mundo y cuyas actuaciones son detectadas por el sistema (de forma directa o indirecta). Esta distinción tampoco es tan clara en determinadas circunstancias. Supongamos un edificio y un sistema que controla las posibles apariciones de incendios y actúa en consecuencia. Posee detectores de humos, de calor, etc. Posee dispositivos para activar los extintores en los puntos afectados y muestra a las personas encargadas de la extinción el lugar de ubicación del fuego. En este caso, los ocupantes del sistema serían ajenos al sistema, mientras que el equipo de extinción formaría parte de él. Como vemos, para llegar a este tipo de distinciones necesitamos conocimiento acerca de la intencionalidad de las personas involucradas.

n  en determinados sistemas el modelo conceptual puede presentar problemas, al no saber exactamente lo que ha de reflejar. Imaginemos un procesador de texto. ¿Qué ha de incluir? :

•       ¿el significado de las palabras escritas ?

•       ¿las letras, palabras y frases, consideradas como objetos en si ?

•       ¿el aspecto visual de las letras, palabras y frases, teniendo en cuenta fuentes, estilos, etc ?

•       ¿la forma en que el procesador maneja las ventanas en el monitor ?

La respuesta a esta pregunta aparece en el concepto de dominio. Los dominios son considerados subsistemas separados. Algunos de los dominios son : dominios de concepto, cuyo objetivo es simular el comportamiento de la situación considerada (en realidad de alguno de sus aspectos). Por otra parte aparecerán los dominios de interacción, con la misión de permitir mantener en sintonía el mundo y el sistema.

En la situaciones en que se usan los dominios, tendremos a un dominio conceptual que aparecerá embutido (rodeado) por dominios de interacción.

Nosotros consideraremos tres tipos de modelos : modelo esencial, modelo de especificación y modelo de implementación.

A.- Modelo esencial

Tiene como objetivo la descripción de alguna situación real o imaginaria (como situación imaginaria, recordemos, por ejemplo, el caso de un video juego). Al construir este tipo de modelos se pretende comprender la situación considerada, estableciendo hechos sobre ella. Las piezas básicas para la construcción de este modelo serán los objetos y los eventos. Los modelos esenciales se construyen dibujando diagramas, interpretados como descripción de conjuntos, funciones y secuencias de eventos con significado en la

situación considerada.

B.- Modelo de especificación

Relacionado con la descripción del sistema a realizar. Hace necesario considerar qué partes de la situación considerada serán contempladas por el sistema. Al igual que en el caso de los modelos esenciales, se usan para su construcción objetos y eventos, y se plasman en diagramas anotados.

Estos diagramas se interpretarán como una descripción del comportamiento de estímulo-respuesta del sistema. Es, por tanto, una descripción del sistema con un alto nivel de abstracción.

C.- Modelo de implementación

Dedicado al establecimiento de patrones de flujo de control dentro del sistema. Para su construcción se usan objetos y mensajes. Las interacciones entre objetos se producen mediante envío de mensajes entre ellos.

Se muestran mediante diagramas anotados, aunque tendrán una mayor riqueza que en los modelos anteriormente considerados.

La siguiente figura muestra las relaciones existentes entre ambos tipos de modelos :

4.- Modelos esenciales

El propósito de los modelos esenciales es comprender una situación, real o imaginaria.

Los elementos constituyentes de este tipo de modelos, como ya se comentó, son objetos y eventos. Su interpretación es un conjunto de hechos sobre la situación considerada.

La construcción de un modelo esencial puede suponer el establecimiento de los hechos sobre una situación preexistente, o puede involucrar el diseño de los hechos sobre una situación aún no construida. Por ejemplo, en el desarrollo de un video juego, en que unos alienígenas compiten por la posesión de un mundo. Esta situación imaginaria contiene hechos que habrán de ser determinados para la construcción del modelo.

Los hechos a establecer son los siguientes :

n  los posibles estados en que se puede encontrar la situación considerada

n  el conjunto de eventos que producen cambios entre estados

n  las posibles secuencias de eventos que pueden ocurrir

Los estados de una situación vienen descritos en términos de objetos, que poseen propiedades, y relaciones entre ellos. Un estado consta de un conjunto de objetos, cada uno de ellos con sus propiedades específicas, participando en relaciones particulares entre sí.

Una tarea en la construcción de este tipo de modelos es considerar qué tendremos en cuenta. En cualquier situación pueden existir infinidad de fenómenos que pueden ser percibidos y que podrían ser incluidos en el modelo. Para tomar esta decisión se tendrá en cuenta el propósito para el que se construye el modelo y se seleccionará todo aquello que resulte relevante.

Los eventos pueden incluir información o no. Los eventos son instantáneos y ocurrieron o aún no han ocurrido. No hay un tiempo presente para ellos.

El modelo esencial no describe relaciones causa-efecto. No es de interés la causa que provoca cambios en una situación, si no determinar, descubrir secuencias de eventos que pueden suceder y qué otros no. Por ejemplo, un interruptor con dos posiciones podrá estar en encendido o en apagado. No es posible la ocurrencia de dos eventos de encendido si entre ellos no se intercala uno de apagado.

Por supuesto, el modelo esencial ha de reaccionar ante los eventos produciendo cambios de estado, de forma que en todo momento refleje el estado de la situación modelizada.

5.- Modelos de especificación

Tiene como objetivo la descripción del sistema a realizar, establecer qué es lo que hará. Este modelo recogerá los estados en que puede encontrarse el sistema, y el conjunto de estímulos que provocan cambios de estado y generación de respuestas.

También se construye, igual que el modelo esencial, con objetos y eventos. Los formalismos usados en ambos tipos de modelos son muy parecidos.

Las principales diferencias entre ellos radican en :

n  el modelo de especificación puede generar eventos por sí mismo (al considerar que invocaciones a determinadas funciones han de ligarse con la ejecución de determinadas tareas)

n  un modelo de especificación puede dejar indefinida la respuesta ante determinados eventos (ya que en el sistema que nos interesa no se producirá respuesta ante ellos)

Un modelo de especificación describe el software a un alto nivel de abstracción, que no incluye consideraciones sobre control de flujo, concurrencia, detalles de interfaz de usuario, etc.

Para crear un modelo de especificación se hace necesario establecer la frontera entre el sistema y el mundo. La construcción de este modelo implica pensar en profundidad en la forma en que interactuan el sistema y la situación considerada. En general requerirá el diseño de un completo interfaz de usuario, junto con las tareas que la harán operativa. En esta fase se suelen utilizar técnicas de prototipado.

Este modelo ha de establecer también que tipos de objetos tienen influencia en qué tipos de comportamientos.

Con anterioridad se había comentado la importancia de la reutilización. Esto se aplica tanto a las fases de análisis como de implementación. De este tipo de modelos deberían salir abstracciones "robustas" de tipos de objetos, que permitirían su reutilización en otros modelos.

6.- Modelos de implementación

El modelo de implementación describe los objetos que participan en el sistema software y la forma en que se comunican. Para su construcción se utilizan objetos (con tipos, estados y propiedades) y que se comunican mediante paso de mensajes.

Es obvio que se trata del modelo más cercano al sistema final y por tanto, a su implementación real. Por eso en esta fase se han de considerar qué consecuencias tendrá la elección de un determinado lenguaje de programación :

n  qué tipo de librerías existen ya

n  qué particularidades acerca de la herencia, por ejemplo, se presentan en cada lenguaje

Con la aparición de la tecnología orientada a objetos se diluye la distinción entre datos y procesamiento, para dar paso a la establecida entre el interior y el exterior de un objeto.

Los objetos encapsulan datos junto con operaciones que actúan sobre ellos. La única forma de acceder a los objetos es a través de sus operaciones, que ofrecen servicios a los objetos clientes.

Un objeto puede verse como un mecanismo de estímulo-respuesta, en que un estímulo es un mensaje que provoca la invocación de uno de sus operaciones. Como respuesta se producirán una serie de mensajes enviados por este objeto a otros, cada uno de los cuales causará, a su vez, sus propias respuestas.

La distinción entre el interior y el exterior de un objeto se pone de manifiesto en el modelo del huevo.

Si un objeto es un huevo, la yema representa los datos del objeto, mientras que la clara representaría las operaciones del objeto. La línea más externa del huevo representa la interfaz que los objetos ofrecen al mundo. Las flechas denotan referencias de un objeto a otro, que siempre concluyen en la línea más externa del huevo destino, indicando que esta es la única parte accesible desde el exterior del mismo. El objeto destino de la flecha es el sumistrador del servicio, y el origen el cliente.

En un modelo de implementación los estímulos externos se convierten en mensajes enviados entre objetos.

Ya se comentó con anterioridad que la tecnología de orientación a objetos pone todo el empeño en la reutilización. Considerando los sistemas bajo la perspectiva de su implementación, esto se consigue gracias a la separación de los objetos entre exterior e interior. En el interior de un cliente se conoce cómo es el exterior de los suministradores con que se relaciona. Cualquier nuevo suministrador que mantenga el mismo exterior que el anterior podrá ofrecer sus servicios al cliente. Esta propiedad se denomina polimorfismo. La idea se pone de manifiesto en el siguiente esquema :

7.- Vistas y notaciones

Cada uno de los modelos se expresa en una serie de vistas, ofreciendo cada una diferentes aspectos del modelo al que pertenecen. Las dos vistas más importantes son :

n  vistas de tipo : consideran los tipos de objetos que intervienen en el modelo, sus propiedades y las relaciones entre sí

n  vistas de estado : muestran como cambian los estados de los objetos como resultado de la ocurrencia de eventos

- TEMA 5 -

DESCRIPCIóN DE LA ESTRUCTURA : BASES

1.- Objetos, valores y eventos

El mundo real es algo muy complicado. Como productores de software estaremos obligados a construir modelos de él y a conseguir que cobren vida.

Afortunadamente, los modelos a construir son parciales, referidos al aspecto que nos interesa automatizar. Para reflejar esta idea, se hablará de modelización de situaciones de la realidad. Por situación se entenderá un conjunto de objetos y ocurrencias que describen alguna actividad. Hay que considerar que las situaciones se construyen siempre con un objetivo determinado. Por esto, ante objetivos distintos, el mismo conjunto de objetos y ocurrencias darán lugar a situaciones diferentes.

Para realizar las modelizaciones usaremos objetos y eventos.

Los objetos tienen identidad propia : un objeto siempre puede distinguirse de otro. Los objetos presentan propiedades observables : tamaño, altura, peso, color, etc.

En algunas ocasiones puede resultar interesante establecer relaciones matemáticas entre propiedades de los objetos : por ejemplo, entre tamaño y volumen. Estas relaciones de denominan invariantes lógicas. Algunas de las propiedades de un objeto pueden ser, a su vez, objetos. Suponer el caso de que consideremos como objetos botellas de vidrio. Una de las propiedades de este objeto puede ser el fabricante que las realizó (otro objeto). Las propiedades que son otros objetos reciben el nombre de asociaciones. Reseñar también que las propiedades de los objetos pueden ir variando a lo largo del tiempo. Por ejemplo, una de las propiedades de un fabricante puede ser su sede social y ésta puede variar con el tiempo.

Los eventos provocan la aparición de nuevos objetos, cambios de estado en ellos, cambios en los valores de sus propiedades, etc. Como ya se comentó, los eventos no tienen duración.

2.- Tipos

Para soportar los modelos necesitamos descripciones genéricas. Si estamos considerando botellas, por ejemplo, la siguiente figura describe la relación entre ellas y sus productores.

Sin embargo, esta representación no considera situaciones en que estén involucradas tres botellas o dos productores.

Por tanto, se observa la necesidad de descripciones genéricas en la construcción de modelos. Estas descripciones sólo podrán obtenerse a través de la generalización. Es decir, se necesita algún concepto que soporte la descripción de todos los posibles objetos (en cualquier número) dentro de la situación considerada, junto con conceptos que permitan incorporar todas sus propiedades. Se denominará a este conjunto de conceptos tipo de objetos. Un tipo de objetos representa a toda una clase particular de objetos. Es una idea muy cercana, conceptualmente hablando, a la de clase en programación orientada a objetos.

Usando tipos de objetos, la situación anterior se representará, de forma completamente general, mediante el siguiente esquema :

Esta figura está dibujada según la notación OMT. Cada rectángulo representa un tipo de objeto y las líneas entre rectángulos representan asociaciones entre objetos. El nombre del tipo de objetos aparece en la parte superior del rectángulo, separado del resto mediante una línea horizontal. Por convención, los tipos de objetos comenzarán con una letra mayúscula. El resto del rectángulo se utiliza para indicar propiedades del tipo de objetos (propiedades que no son asociaciones) e invariantes lógicas. Este tipo de representación se denomina vista de tipo. Como se observa en el gráfico anterior, las propiedades de los objetos presentan un tipo determinado, que aparece a la derecha del nombre de la propiedad.

El significado de la anterior vista de tipo es que en la situación considerada tendremos objetos del tipo botella y objetos del tipo productor. Esta identificación se hace única y exclusivamente en función de las propiedades que exhiben cada uno de ellos.

Normalmente, para llegar a determinar los objetos que intervienen en la situación considerada, se examinará el vocabulario usado para su descripción, en especificaciones, manuales de operador e indicaciones de los expertos.

3.- Propiedades

Como se ha visto anteriormente, podemos distinguir entre las propiedades que relacionan con otros objetos (asociaciones) y las que no. Este último tipo de propiedades se denominan valuadas.

Aparecerán listadas en la vista de tipo. Cada objeto presenta su propio conjunto de propiedades, representando piezas de información que pueden ser observadas por cualquier otro objeto.

Las relaciones entre propiedades valuadas se representan mediante invariantes lógicas, que aparecen también especificadas junto a la lista de propiedades.

Una propiedad se define especificando su nombre y su tipo, de la siguiente forma :

nombre_de_propiedad : tipo_de_propiedad

Los tipos de propiedad que usaremos más frecuentemente son : número, cadena, fecha y hora.

Algunas de las propiedades pueden estar parametrizadas. Por ejemplo, la propiedad volumen de una botella puede ser dependiente de la temperatura. Esto podría expresarse de la siguiente manera :

volumen(temperatura : número) : número

o también :

volumen(número) : número

si esta especificación no es ambigua.

Las propiedades también pueden ser multivaluadas : pueden consistir en una colección de valores del mismo tipo. Por ejemplo en el objeto Productor podemos considerar como propiedad el tamaño de las botellas producidas. En este caso estaríamos hablando de un conjunto de números. Este conjunto puede aparecer de diversas maneras :

•       como conjunto ordenado de valores, sin permitir valores duplicados

•     como conjunto desordenado de valores, sin permitir duplicados

•     como conjunto ordenado de valores, permitiendo duplicados

4.- Asociaciones

En la figura anterior se muestra una asociación entre objetos. ¿Cual es la forma de interpretar esta asociación ?. Informalmente, su significado es que identificando un objeto de tipo botella, se puede determinar, en virtud de la asociación, el productor que la construyó. De igual forma, identificando un productor se pueden concretar los tipos de botellas que fabrica. Sabemos que en este último caso estamos hablando de un conjunto de tipos de botellas, debido al círculo negro que aparece del lado del tipo de objetos Botella.

Cuando se usa una asociación para identificar los objetos de ambos extremos decimos que la estamos navegando. Cada asociación puede ser navegada en ambas direcciones. En realidad se trata de un par de asociaciones relacionadas, cada una con características diferentes. Para aclarar este aspecto, cuando estamos considerando una dirección particular de navegación nos referimos a los tipos de objetos origen y destino.

Los extremos de las asociaciones pueden anotarse, con una etiqueta que indica el papel jugado por el objeto de un extremo con respecto al objeto del extremo opuesto. Cuando sólo hay una relación de asociación entre dos tipos de objetos, no es obligatorio usar etiquetas. En esta caso el papel de cada tipo de objeto es igual al del tipo de objeto a cada extremo de la asociación, sustituyendo la mayúscula inicial por una minúscula.

Si hay dos o más asociaciones entre dos tipos de objetos, las etiquetas de los papeles resultan esenciales para la comprensión del modelo. En la siguiente figura se presentan dos asociaciones entre los tipos de objetos Botella y Productor. Cada asociación debe tener un único nombre de papel. Para el productor los nombres de papel son produce y almacena. Para la botella serán hecha por y almacenada por. Al ser dos asociaciones diferentes, el productor y almacenista de una botella pueden ser dos objetos distintos (de tipo productor, por supuesto).

La existencia de símbolos en los extremos de las líneas que representan las asociaciones modifican el significado obtenido con su navegación. Una extremos de la línea sin adornos significa que la navegación de la asociación, en esa dirección, conduce a un objeto simple del tipo de objetos de ese extremo. Un círculo negro significa que la navegación conduce a una colección de objetos, es decir, representa un conjunto.. Este tipo de asociaciones se denominan múltiples.

Se usa el término conjunto en su sentido matemático : puede tener cero o más miembros, pero no puede tener duplicados. Como se verá más adelante, se pueden añadir restricciones a la asociación múltiple, para limitar el número de elementos del conjunto representado por el círculo negro. Una particular restricción, que limita el tamaño del conjunto a cero o uno ocurre tan frecuentemente que se proporciona una notación especial para ella :

El círculo blanco en el extremo de una asociación representa una asociación simple opcional. Si identificamos una botella puede ser que tenga una etiqueta o que no tenga ninguna. Reseñar que este esquema no muestra las circunstancias en que es posible la identificación de etiqueta ni aquellas otras en las que no.

Los modificadores de las asociaciones pueden aparecer en ambos extremos de las mismas. Considerar el siguiente ejemplo :

Cada empresa tiene varios empleados y una persona puede estar empleada por más de empresa (tener varios trabajos).

Algunas veces puede ser interesante ser más específico en la especificación de las asociaciones múltiples, indicando la forma en que el tipo objeto origen distingue los objetos del tipo objeto destino. Esto se hace añadiendo un calificador a la asociación. En el extremo origen. Supongamos que cada productor produce únicamente una botella por día. En la figura siguiente se sustituye la asociación por una caja de calificación. El nombre del calificador será el nombre por defecto del otro extremo de la asociación. El calificador tendrá un tipo, que en nuestro ejemplo es una fecha.

La forma de interpretar el calificador sería la siguiente : dado un productor y una fecha, podemos identificar una botella particular (la producida ese día).

Al no tener la asociación ningún modificador al extremo de la botella, se asume que una combinación de productor y fecha conduce a una única botella. Esto no es del todo cierto, ya que el rango de valores de fecha es infinito. De hecho, en cualquier modelo razonable se reflejará el hecho de producción de botellas sólo en determinadas fechas. Aunque se puede usar un calificador que restrinja el número de fechas posibles, la solución óptima se muestra a continuación :

Aunque lo más normal sería que un productor fabrique más de una botella en el mismo día. Esto se representaría mediante la siguiente representación :

Un calificador puede tener más de un parámetro. El tipo de cada parámetro ha de indicarse entre paréntesis.

Un tipo particular de asociaciones es la agregación. Normalmente se alude a esta asociación como relación "todo-parte" o "es-parte-de".

En la notación OMT que emplearemos se representa con un rombo en el extremo de la línea de asociación. Podemos pensar en tres posibles significados para la agregación :

n  una compartición de propiedades. Podemos considerar un coche como una agregación de sus partes. Supongamos para el coche una propiedad que representa su color. De esta forma, las puertas del coche tendrán el mismo color. Es decir, que el color del todo se propaga a las partes. La influencia también puede producirse en sentido inverso. Si cada una de las piezas posee un peso determinado, el peso total vendrá en función del peso de sus componentes. No se empleará este sentido para la agregación que consideraremos.

n  encapsulación. La idea aquí es que el todo encapsula sus partes de alguna manera. Pueden distinguirse dos razones para desear la aplicación de este significado : permitir la construcción de software más robusto y modular y controlar la complejidad del modelo (basado en la idea de composición de los objetos a componentes, que no son conocidos por sus usuarios). Esta idea también se rechaza.

n  dependencias en tiempo de vida. Este es el significado que se dará a la agregación. En este sentido cada parte, en el momento en que es conocida en la situación analizada, aparece conectada con una agregada, y esta relación persiste hasta que alguna de estas dos partes desaparezca. También puede considerarse de la siguiente forma : cuando se crear un objeto agregado se compondrá de una serie de partes que no pueden cambiar durante el tiempo de vida del todo, pero cuando este se destruye las partes pueden formar parte de otro agregado.

La figura siguiente muestra un ejemplo clásico de agregación. Una división es una parte de una compañía. Usando la semántica de la agregación, se puede ofrecer una visión más concreta de esta relación. Cada división pertenecerá sólo a una compañía y debe permanecer asociada a esta compañía durante todo su tiempo de vida (de cualquiera de ellos : empresa o división). Las divisiones pueden crearse y destruirse, pero mientras permanecen no se transfieren a otra compañía. Si la compañía se destruye, también lo harán sus divisiones.

Cambiar el rombo al otro extremo de la asociación cambia completamente su significado.

En este caso se asocia la permanencia de la empresa a la permanencia de sus divisiones. Cuando se crea una empresa ha de asociarse a sus divisiones y no puede cambiarse esta asociación mientras persistan las divisiones y la empresa. La empresa puede asociarse a cualquier número de divisiones, pero este número es fijo en el momento de la creación de la compañía. En el esquema se muestra que cada división se asocia con una compañía, pero no hay ninguna razón por la que la división no puede asociarse a otra empresa si aquella a la que se asocia se destruye.

Las asociaciones pueden poseer sus propias propiedades, como se muestra en la figura siguiente :

Cada asociación entre un empleado y una compañía posee una propiedad de salario. Si una persona tiene más de un trabajo, tendrá una salario en cada una de las empresas en que trabaja. Este tipo de propiedades son más interesantes en asociaciones múltiples en ambos extremos. La propiedad adjudicada a la relación sería, en este caso, difícil de adjudicar a alguno de los extremos. En el ejemplo mostrado, no sería correcto considerar el salario como una propiedad de ninguno de los dos tipos de objetos. Por cuestiones de claridad se ha de evitar que el nombre de la propiedad de la asociación coincida con alguno de los nombres de propiedades ya usados en los tipos de objetos, ni con los nombre de los papeles jugados por ellos.

En principio es posible definir más de una propiedad en una asociación. Sin embargo, en estos casos lo más frecuente es crear un nuevo tipo de objeto y vincularlo a la asociación de la misma forma en que se hacía con las propiedades.

Este nuevo objeto se usará de igual modo que cualquier otro, y podrá tener a su vez sus propias asociaciones con otros objetos. El asociar un nuevo objeto a una asociación introduce un nuevo nombre de "papel" a la misma, pudiendo mostrarse explícitamente en caso de ser necesario. En caso de no hacerse así se aplica el nombre de papel por defecto (el correspondiente al tipo de objeto, con la primera letra en minúscula). Por supuesto, para evitar confusión se evitará introducir nombres de papeles repetidos.

Vamos a considerar las diferencias entre el esquema anterior y el siguiente, que sería una forma más clásica de tratar una relación de "muchos-a-muchos".

En el primero de los gráficos, al navegar la asociación desde Empleado hasta Compañía, se identifican un conjunto de compañías diferentes, por lo que no es posible, en este modelo, definir la situación en que una persona desempeñe a la vez varios trabajos con la misma Compañía. Sin embargo, en el segundo de los gráficos no existe esta limitación, ya que el conjunto de empleos de una persona pueden estar relacionados con la misma empresa.

Para las asociaciones en que aparezcan involucradas ternas de objetos se propone la utilización de relaciones binarias junto con nuevos tipos de objetos que representen explícitamente la asociación. Imaginar la siguiente situación : hemos identificado como objetos en el modelo apellido1, apellido2, nombre. Estos tipos de objetos participan en una asociación que define el nombre de una persona. Una forma de abordar esta situación podría ser la siguiente :

La existencia de una asociación entre dos tipos de objetos define claramente una relación uno a uno. Algunas veces puede ser interesante no ser tan precisos, es decir, establecer la existencia de una asociación entre dos tipos de objetos pero sin especificar su grado de multiplicidad. Esto se consigue mediante el uso del modificador ?. Se observa su uso en el siguiente ejemplo :

En este esquema se ha decidido que cada botella está asociada con un sólo productor, pero no se ha establecido cuántas botellas se relacionan con cada productor. Esto significa que la asociación no puede navegarse hacia el tipo de objeto botella, con total significado, hasta que no se haya decidido el grado de multiplicidad.

También se puede usar este modificador en situaciones en las que no queramos especificar demasiado sobre una asociación.

5.- Extensiones de tipo

Un tipo de objetos puede definirse como un subtipo de otro. Esto se conoce como una relación "es-clase-de". Un subtipo hereda todas las propiedades, limitaciones y asociaciones de su supertipo. Se define el subtipado para indicar concordancia en los objetos. Es decir, si un objeto concuerda con el subtipo también concuerda con el supertipo. En general afirmaremos que el subtipo puede extender las posibilidades del supertipo, pero nunca restringirlas.

Las relaciones de subtipado se indican mediante una línea entre el supertipo y los subtipos, como se indica en la figura siguiente :

La figura anterior muestra que una corporación es un tipo de compañías al igual que lo es una sociedad anónima. Cada objeto de tipo corporación posee una propiedad de número de registro mas todas las propiedades y asociaciones propias del tipo de objeto compañía, como por ejemplo un conjunto de empleados. En este caso el valor de la extensión de tipos es permitir una descripción clara de las diferencias entre tipos de objetos relacionados. También se introduce el concepto de polimorfismo. En este sentido el gráfico anterior muestra que para una persona es lo mismo trabajar para una corporación que para una sociedad anónima.

La figura anterior no implica que todos los objetos que concuerdan con el tipo compañía concuerden con algunos de sus subtipos. Podemos pensar en un objeto de tipo compañía que no sea específicamente ni una sociedad ni una corporación. Se puede introducir una restricción para que todos los objetos que concuerden con el supertipo coincidan con alguno de los subtipos mediante la definición de un supertipo como abstracta. Podemos limitar el tipo de objetos compañía, haciéndolo abstracto, añadiendo un tipo especial de invariante, como se observa en la figura siguiente :

La diferencia entre las dos figuras siguientes puede explicarse mediante diagramas de Venn. En el primero de los modelos los objetos de tipo corporación y sociedad originan subconjuntos disjuntos del tipo de objetos compañía. En el segundo de los modelos los conjuntos disjuntos establecen una partición completa del superconjunto.

La introducción de un subtipo eliminará frecuentemente asociaciones opcionales como se indica en la figura siguiente :

La parte superior del diagrama muestra que cada botella puede tener opcionalmente una etiqueta. En el segundo se expresa claramente que las botellas plásticas nunca tienen una etiqueta, mientras que las de vidrio siempre la tendrán.

6.- Limitaciones e invariantes

Una de las razones por las que el significado de la notación de modelización ha de ser tan precisa como sea posible es permitir que un grupo de diseñadores puedan tener la misma comprensión ante un mismo modelo. Otra, no menos importante es posibilitar la precisión formal de las matemáticas, de la teoría de conjuntos y de la lógica, en conjunción con el modelo.

Un uso importante de las expresiones matemáticas es en la especificación de las invariantes lógicas de tipo. Se trata de expresiones lógicas que han de ser ciertas para todos los objetos del tipo considerado. Algunos ejemplos se muestran en la figura que aparece a continuación.

El tamaño de las botellas ha de ser menor que 100 y no negativo. Con respecto a las otras dos invariantes, se requiere alguna explicación adicional.

La expresión

suma almacena.valor

es una expresión que incluye navegación a través del modelo. Para cualquier productor la expresión "almacena" representa el conjunto de botellas obtenidas mediante navegación, a partir del productor considerado, a través de la asociación etiquetada como "almacena". La adición de ".valor" indica que deseamos trabajar con la propiedad "valor" de las botellas. Finalmente se sumará esta colección de números. En la otra invariante

#producto

indica el tamaño del conjunto de botellas obtenidas mediante la navegación de la asociación etiquetada como "producto". El operador # permite obtener el tamaño de cualquier colección.

La forma de entender estas invariantes es pensar en ellas como una indicación de que un objeto conoce algo sobre un valor.

Las restricciones sobre el rango de valores pueden especificarse sobre la definición de la propiedad, en vez de como invariantes, mediante el uso de subrangos. Los subrangos tienen la siguiente forma :

m..n

donde m y n son enteros positivos o expresiones que conducen a este tipo de valores. En el caso en que m=n, el entero o el símbolo puede utilizarse sin más, por ejemplo 6. En el esquema anterior, la propiedad de tamaño puede definirse como :

tamaño : 0..99

y eliminar las invariantes.

También pueden restringirse las propiedades individuales, de forma que sus valores permanezcan fijos durante el tiempo de permanencia del objeto al que pertenecen. Esta limitación se indica mediante la palabra const.

Otra posible limitación es la de requerir a una propiedad que contenga un único valor para cada objeto del tipo considerado. Esta limitación se consigue mediante la invariante especial de tipo unique. En la siguiente figura se limita la propiedad tamaño mediante ambas invariantes.

El valor especial nil es un miembro de todos los objetos y tipos de valor, y representa una propiedad indefinida o no establecida. Las propiedades que pueden tomar este valor se denominan opcionales, y deben especificarse como tales mediante la correspondiente invariante de tipo, como puede verse a continuación (optional).

Si una propiedad no está definida como opcional, no podrá tomar este valor.

Como hemos visto, las restricciones indican limitaciones que afectan al modelo. Las invariantes de tipos de objetos son sólo una forma de restricción, que aparecen especificadas dentro de las cajas usadas para los tipos de objetos. Las restricciones que aparecen fuera de las cajas de los tipos de objetos aparecerán encerradas entre corchetes. Se pueden escribir de forma informal, como una anotación, o usar una notación más precisa que se apoye en la navegación y en símbolos matemáticos.

Un tipo común de restricción es la que limita el tamaño del conjunto de objetos involucrados en una asociación. Una asociación sin limitación alguna se representa, como ya se vio, mediante un círculo negro en uno de los extremos de la línea que representa la asociación. También se ha considerado el modificador que limita el tamaño del conjunto a 0 ó 1, y se trata del círculo blanco. Cualquier otra limitación ha de expresarse mediante anotaciones situadas cerca del círculo negro. Las restricciones sobre multiplicidad se especifican mediante subrangos. En el esquema siguiente, cada persona puede trabajar entre 0 y seis compañías. Cada compañía tiene una propiedad representando el máximo número de personas que puede tener en plantilla. Esta propiedad se usa para especificar un límite para el conjunto de empleados. Como un caso especial, cuando se necesita únicamente un límite inferior, puede ponerse a continuación el signo +, como por ejemplo [1+].

Otro tipo de limitación que puede aplicarse a una relación especifica el orden de los elementos involucrados en ella. Por defecto la navegación de una relación conduce a un conjunto desordenado y sin duplicados. Esto puede modificarse mediante las siguientes restricciones :

nombre	sintaxis	ordenado ?	duplicados ?
bag	[bag]	NO	SI
sequence	[seq]	SI	SI
sort	[�especif. de ordenación']	SI	SI

La especificación de ordenación puede ser informal o formal. Si la especificación es formal, ha de declarar dos variables del tipo de objetos considerado (normalmente a y b) e incluir una expresión lógica que las relacione. En la asociación, a aparecerá antes que b si la expresión es cierta.

En el siguiente modelo se observan limitaciones mediante sequence y sort. En la asociación ordenada las botellas aparecen ordenadas en orden descendente de tamaño. El contenido de la cinta transportadora se define como una secuencia, permitiendo que haya otras dos asociaciones que definan el primer y último elemento de la secuencia. Estas asociaciones serán opcionales ya que la cinta puede estar vacía.

También existirán restricciones entre dos o más asociaciones. Se representan mediante flechas sombreadas en la literatura sobre el tema, con una descripción de la limitación que suponen, encerrada entre corchetes.

En el esquema siguiente se muestra una restricción entre las asociaciones de producción y almacenaje, indicando que el número de botellas almacenado por un productor ha de ser menor de la mitad de las que produce. Es equivalente a introducir la restricción como invariante en el tipo de objeto productor. Sin embargo se prefiere introducirla como restricción entre asociaciones para limitar el acoplamiento entre el tipo de objetos y sus asociaciones (es decir, si se introduce como invariante en el tipo de objetos tendremos conocimiento sobre la asociación implícito en la descripción del tipo de objetos, algo que no es deseable).

Las restricciones entre asociaciones son direccionales. En la figura que sigue la dirección viene determinada por la semántica de la restricción. Está limitando el nivel de almacenaje del productor (que serán botellas). La restricción, por tanto, se refiere a la navegación de la asociación que tiene como origen a productor y como destino a botella. Es una consecuencia de las asociaciones restringidas que conducen al mismo objeto origen cuando se navegan en sentido inverso (del destino al origen). En nuestro existe la limitación de que para caba objeto de tipo botella, su productor y almacenista serán el mismo objeto de tipo proveedor.

Las limitaciones de subconjunto son un tipo especial de limitaciones, que ocurren tan frecuentemente que se proporciona para ellas una sintaxis especial. Una restricción de subconjunto especifica que el conjunto de objetos alcanzados por una navegación de la asociación son un subconjunto de los alcanzados por la otra. En la figura siguiente se especifica que el stock del almacenista es un subconjunto de toda su producción. Observar que la punta de flecha apunta al "superconjunto".

Esta restricción también es direccional : de productor a botella. Esto se debe a que vincula los productos y stock del productor. Este tipo de restricciones sólo pueden aplicarse a dos asociaciones múltiples.

En el caso en que tengamos asociaciones 0-1 en cada extremo (círculos blancos) los conjuntos tendrán ó 0 ó 1 elemento, en ambos sentidos de la navegación. En este caso, para definir este tipo de restricciones se tendría que especificar el sentido de navegación, lo que se indicaría de la forma :

[Tipo objeto origen :: subconjunto de]

Otra limitación de subconjunto es aquella en que deseamos indicar que el objeto alcanzado por una navegación, a través de una asociación simple u opcional, es un miembro del conjunto alcanzado por una asociación múltiple. En este caso se reemplaza la palabra subconjunto por miembro.

7.- Tipos de estado

Consideremos un ejemplo anterior bajo una nueva perspectiva.

Al ser el salario de una personal una propiedad valuada, se ha colocado dentro del tipo de objetos persona. Esta es una mala opción, ya que ha de estar indefinido (nil) cuando la persona no tiene trabajo. Una opción mejor sería ligar esta propiedad a la asociación, pero también se podría pensar en un modelo más descriptivo creando dos subtipos de persona (uno para personas con empleo y otras para quienes no lo tienen).

En nuestro modelo se ha situado la propiedad salario relacionada con el tipo de objeto persona empleada, y se elimina también la asociación opcional y reemplazarla por otra más restrictiva. Sin embargo, este modelo presenta un problema : una persona desempleada lo será para siempre.

El significado de nuestros modelos es tal que los objetos no pueden cambiar el tipo de objetos al que pertenecen, durante todo su ciclo de vida. De esta forma, una persona desempleada nunca podrá ser empleada.

Para evitar este tipo de situaciones se introduce el concepto de tipos de estado, que se comportan igual que los subtipos normales, ya vistos, pero que se consideran como posibles estados distintos del supertipo al que pertenecen (considerar al supertipo, por ejemplo, como una máquina de estados). Los objetos no se crearán de acuerdo a ningún tipo de estado : la relación con un estado u otro cambiará a medida que cambia el estado del objeto. Cada tipo de estado ha de aparecer en la vista de estados.

Los tipos de estado no pueden tener tipos normales como subtipos, pero sí pueden tener otros tipos de estados. Esto representa una estructura anidada de estados, con lo que si el objeto se encuentra en el estado representado por un tipo de estado, debe estar siempre en alguno de los estados representados por sus subtipos.

Un grupo de tipos de estado conectados a su supertipo representa un conjunto exclusivo de estados (sólo podrá estar en uno). Un tipo de estados puede tener a su vez varios grupos conectados. El objeto se encontrará en un estado de cada uno de los grupos.

El uso de tipos de estado establece un enlace directo entre las vistas de tipos y las vistas de estado. Lo normal será empezar considerando a los objetos como tipos de objetos normales y si se manejan mejor como estados, se manejarán como tipos de estado.

- TEMA 6-

DESCRIPCIóN DE LA ESTRUCTURA : AÑADIENDO MÁS DETALLE

1.- Introducción

En este capítulo se añadirá más detalle a los elementos de construcción del modelo esencial.

2.- Navegación

En este punto se verá la notación adecuada para realizar la navegación sobre los modelos esenciales.

Cada vista de tipos ha de originar un espacio de nombres separado, es decir, dentro de ella los únicos nombres que pueden ser referenciados son aquellos que aparecen en el diagrama. Todas las expresiones de navegación se escriben desde la perspectiva de algún objeto, perteneciente a uno de los tipos de objetos que aparecen en el diagrama.

Hemos de definir el conjunto de nombres que pueden usarse por un determinado objeto :

•       el de las propiedades del tipo de objetos al que pertenece y las de su supertipo (si lo hubiere)

•       los nombres de papel de las asociaciones

•       nombres de calificadores de los tipos y de los supertipos

•       los nombres de propiedades de las asociaciones

•       los nombres de los tipos de estado

Según se ha comentado antes, para el tipo de objetos Productor, los siguientes nombres están baso su ámbito de uso :

•       nivel_prod : propiedad definida localmente

•       facturación : propiedad definida por el supertipo

•       producto : nombre de calificador de la asociación entre Productor y Botella

•       empleado : nombre de asociación derivada, propia del tipo de objetos Persona

•       empleo : nombre de papel implícito del tipo de asociación de la asociación de empleo

Para escribir una expresión de navegación se ha de comenzar con el nombre de un objeto perteneciente a uno de los tipos considerados en el diagrama. Supongamos que m es un objeto de tipo Productor.

Esta expresión se escribiría de la forma :

m : Productor

indicando que m es una variable que se refiere a un objeto del conjunto de objetos que conforman el tipo de objetos Productor. Se utiliza el tipo de nombre para representar el conjunto de objetos sobre el que se trabajará. Dada la expresión anterior

m.nivel_prod

representa el nivel de producción del objeto m. La expresión

m.empleado

representa el conjunto de emplados del Productor m.

Esto mismo también puede expresarse de la siguiente manera :

Productor :: empleado

sin necesidad de aludir a ninguno de los objetos concretos de tipo Productor.

Una vez que hemos accedido a objetos de tipo Persona, a través de la navegación desde Productor, se puede hacer alusión al conjunto de nombres en el ámbito de este tipo de objetos. Así

Productor :: empleado.banco

que alude al conjunto de bancos de los empleados de un objeto del tipo Productor. A medida que vamos navegando, varía el ámbito de nombres a usar, para adaptarse al ámbito de los objetos considerados en ese punto.

Ya que Productor :: empleado representa un conjunto, cualquier navegación posterior se aplicará a cada uno de los miembros de dicho conjunto y el resultado será otro conjunto de objetos del tipo alcanzado por la navegación.

Se aplican reglas diferentes cuando se acceden propiedades valuadas :

Productor :: empleado.nombre

representa el conjunto de nombres de los empleados de un productor. Hemos de considerar que obtenemos un conjunto de propiedades y no un conjunto de objetos. En este caso en concreto se tratará de un bag, que no ofrece ordenación y perimite duplicados.

En la expresión

sum ( Compañía :: empleo.salario )

se recoge la suma de los salarios pagados a los empleados de una Compañía.

Si cada navegación nos conduce a un conjunto, el resultado final será la unión final de ellos. Si consideramos

Productor :: empleado.banco.número_cuenta

representa el conjunto de todas las cuentas bancarias de todos los bancos usados por todos los empleados de un productor.

Para navegar, en el esquema anterior, la asociación que presenta el calificador, se necesita un parámetro :

Productor :: produce(1-Enero-1997)

para obtener el conjunto de botellas hechas en ese día.

Las asociaciones opcionales son algo más complicadas, ya que la navegación

Botella :: etiqueta

puede conducir o no a un objeto del tipo Etiqueta. Si no hay etiqueta asociada, esta expresión conduce a nil.

Esto conduce a alguna confusión en expresiones como :

Productor :: produce(1-Enero-1997).etiqueta

al conducir, en su primera parte, a un conjunto de botellas. Al acceder a las etiquetas tendremos un conjunto en el que aparecerán algunos objetos de tipo Etiqueta y valores nil. La solución es considerar únicamente los objetos de tipo Etiqueta accedidos.

Consideremos algunas otras expresiones de navegaciones :

Compañía :: empleo.oficina_de_empleo Conjunto de oficinas de empleo donde se formalizaron los empleos de la Compañía.

Empleo :: empleado. La persona asociada con uno de los empleos. La navegación a partir de un tipo propio de una asociación conduce siempre a un objeto simple.

OficinadeEmpleo :: empleo.empleado.nombre. Nombre de todos los empleados de empleos formalizados en una oficina de empleo.

Etiqueta :: botella.productor. Productor de la botella que presenta la etiqueta.

Las siguientes expresiones serán inválidas, como se explica a continuación :

Persona :: compañía.nivel_prod. Las propiedades de los subtipos no son accesibles para los supertipos.

Compañía :: salario. No se puede acceder directamente a una de las propiedades de un tipo de objetos vinculado a una relación. Habría que hacerlo a través de un objeto de tipo Empleo.

Productor :: botella. El acceso a los objetos de tipo Botella ha de hacerse a través del calificador.

Sea p una persona y c una compañía, que será una de las que ofrece empleo a p. Nos interesa acceder a la fecha en que comienza en trabajo se p para dicha compañía. Esto se hará de la forma siguiente :

p.empleo(c).comienzo

El significado sería : para la persona p selecciona el empleo que le asocia a la compañía c y obtén la fecha de comienzo.

Consideremos ahora el siguiente modelo simplificado.

En este modelo, si queremos, a partir de un objeto de tipo Empleo, obtener el conjunto de botellas producidas por el productor que emplea, en la fecha de comienzo del empleo, podríamos poner :

Empleo :: emplea.produce(comienzo)

pero la fecha de comienzo no está en el ámbito del productor, que es el ámbito que se accede a este dato.

No se puede usar

Empleo :: emplea.produce(empleo.comienzo)

porque empleo.comienzo conduce a una colección de fechas y no a una sola. En este caso se empleará el identificador especial self, que alude al objeto en el que comienza la navegación (en este caso algún objeto de tipo Empleo, anónimo). La expresión correcta sería :

Empleo :: emplea.produce(self.comienzo)

En este mismo ejemplo, veamos la forma de escribir una expresión de una navegación en que dada una persona nos permita obtener el conjunto de botellas producidas por todos aquellos productores que le han contratado, en las fechas de comienzo de sus trabajos. El problema vuelve a presentarse en la necesidad de especificar la fecha de comienzo de trabajo adecuada para cada uno de los productores. Si deseamos obtener este conjunto de botellas, podría obtenerse mediante una expresión de conjunto :

É{ e : Persona :: empleo • e.emplea.produce(e.comienzo) }

Lo lógico sería modificar el esquema para facilitar la obtención de este conjunto (recordar que esto sería necesario sólo en el caso en que sea importante la recuperación del conjunto).

Tras esta modificación, la expresión de navegación sería :

Persona :: empleo.primera_botella

A veces la modificación de los modelos resulta necesaria para evitar expresiones de navegación complejas, que producen un acoplamiento indeseable entre el tipo de objetos de comienzo y final de la navegación. Aquí resulta importante reseñar la importancia de la encapsulación en las tecnologías de orientación a objetos. Es decir, las propiedades de un objeto permanecen embebidas en él y accesibles a otros tipos de objetos de forma directa mediante sus funciones de interfaz.

Por tanto, en general, han de evitarse las expresiones de navegación largas. En la medida de lo posible se intentará limitar el conocimiento de un tipo de objetos a los detalles de aquellos tipos con los que está íntimamente relacionado. Las expresiones largas pueden descomponerse añadiendo propiedades derivadas y asociaciones.

3.- Asociaciones derivadas

Una asociación puede definirse en términos de otra o una colección de ellas. Las asociaciones derivadas deben estar acompañadas por una anotación, entre corchetes, que indique el path de navegación. La mejor forma de hacerlo es formalmente, usando una expresión de navegación. Aunque la expresión definirá un camino de navegación, la relación es navegable en ambos sentidos.

Consideremos el modelo siguiente :

En esta figura la asociación entre OficinadeEmpleo y Persona es derivada. También la que existe entre OficinadeEmpleo y Compañía, en la que se seleccionan todas las compañías asociadas a una oficina de empleo, con una facturación por encima de 1000000.

El conjunto de inicio para la selección se define por la expresión normal de navegación (OficinadeEmpleo :: empleo.emplea) y sobre ella un predicado lógico selecciona los miembros requeridos.

Tanto las asociaciones derivadas como las restricciones de conjuntos entre asociaciones, proporcionan formas de especificar un conjunto de objetos como un subconjunto de otro. A su vez, la asociación derivada proporciona una manera de determinan los miembros del subconjunto que define.

A menudo se desea construir asociaciones derivadas en las que la derivación es una función del estado de un conjunto de objetos. Vamos a considerar el siguiente modelo :

Una oficina de empleo se asocia con un conjunto de clientes, que son personas. Hay un subconjunto de estos clientes que son, en un instante determinado, desempleados. La asociación derivada representa este subconjunto. La expresión

p en PersonaEmpleada

da cierto si el objeto p está en el estado de persona empleada. Ya que la asociación derivada tiene como destino este tipo de estado, hay un término en la expresión de la derivación que contiene información redundante y podría escribirse como :

[{p : OficinadeEmpleo :: cliente}]

ya que todos los objetos alcanzados por la navegación de la asociación conducen a personas en estado de empleo. Aunque se pueda expresar en forma reducida, se prefiere la expresión completa, al definir la navegación de forma más completa.

4.- Asociaciones recursivas

Es bastante frecuente encontrar situaciones en que ambos extremos de una asociación estén conectados al mismo tipo de objeto. Las asociaciones que cumplen esta condición se denominan recursivas.

Para ilustrar la interpretación de estas asociaciones se presentarán una serie de ejemplos, considerando el tipo de objeto persona.

Cada hijo tiene una madre y una madre puede tener varios hijos (en realidad de 0 a n).

Otra asociación recursiva respecto del tipo de objeto Persona es aquella que se establece entre doctores y pacientes.

Cada persona puede tener o no doctor. Una persona puede tener pacientes (si es doctor). Para el caso de los no doctores la relación también vale, ya que el extremo de la asociación relacionado con el papel de paciente presenta el modificador círculo negro, que indica un conjunto de 0 a n elementos.

Algunas asociaciones recursivas son inherentemente simétricas. Consideremos la asociación que representa la relación entre cónyuges. En estos casos aparecerá el mismo nombre de papel a ambos lados de la asociación. Además, al tratarse de una asociación simétrica, debe aparecer la misma multiplicidad en ambos extremos.

Esta asociación puede convertirse fácilmente en una asociación 1 a 1,.como se ve a continuación.

Asociaciones de muchos a muchos también son frecuentes. Un ejemplo sería la relación de amistad. Se asume para este modelo que la amistad es mutua, es decir, si Pepe es amigo de Juan, Juan es amigo de Pepe.

5.- Subtipos

Habíamos considerado como los tipos de objetos pueden definirse como subtipos de otro. En los ejemplos mostrados anteriormente, los conjuntos formados por los subtipos resultan disjuntos. Podemos encontrar situaciones en que no ocurra lo mismo.

Veamos un ejemplo :

Puede existir un objeto que concuerde tanto con el tipo Productor como con el tipo Vendedor. La relación matemática establecida entre los conjuntos representados por los distintos tipos de objetos aparece a renglón seguido :

Otro ejemplo de esta situación sería la siguiente :

En este caso, los diagramas de Venn correspondientes serían :

También podemos encontrar la situación en que un tipo de objeto sea "una clase de" más de un tipo distinto. Por ejemplo, imaginar que queremos modelar la siguiente situación : se considera tanto a los comerciantes como a las compañías como conceptos diferentes y además se decide que un productor será ambas cosas a la vez. Esto se muestra en la figura siguiente :

Un tipo de objeto con múltiples supertipos "hereda" la unión de las propiedades, limitaciones y asociaciones de estos. De esta forma, un productor tendrá tanto un valor de stock como fecha de apertura y facturación. Por esta razón no debe de haber ningún conflicto entre los conjuntos de nombres usados por los supertipos.

Es perfectamente válido que dos supertipos, a su vez, sean subtipos de otro supertipo. Es decir :

Las relaciones entre los tipos de objetos se muestran en el diagrama de Venn que aparece a continuación.

Tanto Productor como TiendaMinorista son especializaciones de Comerciante, pero es posible definir objetos que concuerden con ambos, como puede ser una TiendaFábrica (tienda en que la tienda vende sus propios productos). Esto no sería posible en el caso en que TiendaMinorista y Productor fuesen subtipos disjuntos, unidos a Comerciante mediante un único triángulo.

Resulta claro que la tienda de una fábrica tiene una propiedad de nivel de producción y una propiedad de superficie. Pero ¿cuántas propiedades de valor de stock y de fecha de apertuta tendrá ?. Podemos considerar las dos situaciones siguientes :

n  el valor de stock será el total de los stocks de minorista y de productor

n  puede que se desee contemplar las fechas de inicio de ambas actividades por separado

En nuestro caso, consideraremos que TiendaFábrica sólo hereda las propiedades de Comerciante una vez.

La anulación ocurre cuando un subtipo redefine una característica de su supertipo. La definición dada por el subtipo reemplaza y oculta, a partir del subtipo y de sus subtipos, la definición dada por el supertipo. La anulación requiere un gran cuidado, ya que hay que asegurar que los subtipos se mantienen de acuerdo a su supertipo, ya que se debe mantener el principio de que los subtipos se mantienen de acuerdo a su supertipo. Dentro de anulación hay que distinguir entre anulación de asociaciones y anulación de propiedades.

n  Anulación de asociaciones

Ocurre cuando el subtipo tiene una asociación con el mismo tipo con el que la mantiene su supertipo, con el mismo nombre de papel. Podemos considerar varias razones para hacer esta redefinición :

•       cambiar las limitaciones de multiplicidad

•       cambiar los tipos de objetos asociados, para que sean subtipos

•       cambiar restricciones de agregación

Consideraremos el ejemplo siguiente :

En este caso se redefine la asociación entre botella y etiqueta para cambiar las restricciones de multiplicidad. Una botella puede tener o no una etiqueta. Sin embargo, una botella de cristal siempre la tendrá. La limitación de multiplicidad ha pasado a ser [1] frente a la anterior [0..1]. Esta es una limitación válida, ya que [1] entra dentro del rango [0..1]. Recordar que en estos casos el rango especificado por el subtipo ha de ser un subrango del supertipo. El tipo de objetos de botellas de plástico no se ve afectada por la redefinición : es decir, heredan la asociación de su supertipo.

En la siguiente tabla se muestran algunos casos válidos de cambio de multiplicidad :

Rango de supertipo	Rango del subtipo	Válido ?
sin definir	[0..7]	OK
[1..20]	[10..20]	OK
[1..20]	[0..20]	NO
[1]	[0..1]	NO

El subtipo hereda en nombre de papel en la asociación, y no debe sustituirlo. En realidad, se podría deducir que la asociación entre botella de plástico y etiqueta es una redefinición (incluso si no estuviese marcada), ya que en caso de no serlo existirían dos asociaciones entre botella de cristal y etiqueta, una de ellas heredada, lo que no es posible. Para mejorar la legibilidad del esquema, se introduce la flecha que indica que una asociación es una redefinición de la otra.

Con respecto a la redefinición de la asociación podemos considerar dos situaciones diferentes. El diseñador puede optar entre redefinir ambos extremos de la asociación o sólo uno. Veamos las implicaciones de cada una de estas asociaciones (tienen un alto grado de importancia en la posterior funcionalidad a conseguir).

En nuestro caso (ejemplo anterior) se ha optado por redefinir la asociación en el extremo de etiqueta, únicamente. Esto se representa mediante la X que aparece del extremo de botella de cristal. Esto significa que no se introduce un nuevo nombre en el espacio de nombres del tipo de objetos etiqueta : por tanto, no se puede navegar de etiqueta a botella de cristal (este nombre no es accesible). Es decir, la asociación ha sido redefinida para el subtipo únicamente.

Si se elimina la X, el tipo botellas de cristal es accesible desde el tipo de etiqueta. Esto nos indica que las etiquetas nunca asociarán a botellas de plástico. El nombre de papel de botella permanece en el espacio de nombres de etiqueta, por lo que las navegaciones de esta asociación conducen a botellas y no a botellas de cristal. Sin embargo, ahora sí se puede usar el nombre del tipo botellas de cristal, para navegar la asociación redefinida.

La redefinición de los extremos de las asociaciones que llevan a subtipos pueden tener impacto en otros subtipos. Consideremos el ejemplo anterior. Ya que las etiquetas nunca se asocian a botellas de plástico, se ha redefinido, en realidad, su rango de participación en la asociación. En este caso no hay problemas, ya que el nuevo rango es [0], que entra dentro del rango [0..1] inicial. Pero puede haber casos en que se rompan las restricciones de multiplicidad.

Pero imaginemos que la multiplicidad de la asociación entre botella y etiqueta fuese [1+]. En este caso, la introducción de una redefinición (sin X) conduciría a un modelo incorrecto, ya que no es cierto que todas las botellas tengan al menos una etiqueta.

Veamos ahora un ejemplo de redefinición en que se cambian los tipos asociados. Se muestra en el ejemplo siguiente :

Aquí queremos mostrar que mientras que las botellas pueden tener etiqueta o no, pero si son de cristal tendrán etiquetas de papel y si son plásticas tendrán etiquetas de este mismo material. Aquí se ha redefinido la asociación en ambos sentidos, por lo que se puede navegar en ambas direcciones. Los nombres de papel se heredan de la asociación principal. Así en la asociación entre botellas de cristal y etiquetas de papel los nombres de papel serán : etiqueta y etiqueta de papel (recordar que cuando no se explicitaban los nombres de papel se usan los de los tipos asociados).

Navegando desde botella, en la asociación con etiqueta, obtendremos objetos de tipo etiqueta ( y no se puede asumir concordancia con alguno de los tipos de etiquetas). De igual manera, navegando desde botella de cristal, usando el nombre de papel de etiqueta de papel, obtendremos siempre objetos del tipo de etiquetas de papel.

Este tipo de modificaciones suele tener por objetivo el añadir más detalle a la situación modelizada, más que definir nuevas características.

n  Anulación de propiedades

Las propiedades definidas para el supertipo son heredadas por los subtipos, y estos, en general, no deben cambiarlas. Lo que sí se puede hacer es variar o añadir modificaciones sobre ellas.

Los tipos de las propiedades no pueden altrerarse.

Las propiedades invariantes pueden modificarse para afinarlas aún más, pero no se pueden violar. Es decir, la invariante del subtipo ha de implicar la limitación del supertipo. Por ejemplo :

Restricción del supertipo	Restricción del subtipo	Válido ?
x > 3	x > 4	OK
x > 3	x > 2	NO

Los tipos de las propiedades de los subtipos pueden ser modificadas de acuerdo a los mismos criterios señalados anteriormente. Por ejemplo una propiedad definida en el supertipo como entero puede definirse como un rango [1..10] en el subtipo, ya que se trata de un subrango de enteros.

6.- Significado de invariantes

En la figura siguiente se muestran dos invariantes sobre una empresa :

La primera indica que el coste de las nóminas es la suma de los salarios de todos los empleados. La segunda dice que la propiedad coste de esposos se obtiene mediante la suma de los salarios pagados a todos los empleados cuyos esposos trabajan para la misma empresa. Nótese que self se usa para asegurar que el esposo trabaja para la misma compañía y para seleccionar el empleo correcto. Recordar que self se refiere al objeto en el que comienza la expresión de navegación. Como buscamos empleados, la navegación ha de partir de Empresa. Por tanto, self se refiere a un objeto arbitrario de tipo Empresa. Este objeto ha de pertenecer al conjunto de empresas que dan trabajo al empleado considerado (p). Al mismo tiempo se utiliza para determinar el empleo. Recordar que por la primera expresión de navegación se tiene que p es una persona trabajando para una empresa (self) en concreto. En esta asociación aparece un empleo determinado y de ahí nos interesa la propiedad salario.

- TEMA 7 -

DESCRIPCIóN DEL COMPORTAMIENTO

1.- Introducción

La vista de tipos proporciona la anatomía del modelo y ha de ser complementada por alguna otra que describa el comportamiento dinámico.

Este es el objetivo de este capítulo : definir el comportamiento dinámico del modelo. El modelo esencial ha de describir todas las formas en que la situación modelizada puede cambiar, definiendo todas las posibles secuencias de eventos.

2.- Eventos

Los diagramas de tipos consideran los posibles estados de una situación, en términos de configuración de objetos, propiedades y asociaciones. Para completar este modelo necesitamos considerar eventos, que provocan cambios de estado en las situación modelizada.

Sin eventos, nada sucedería. Aunque los eventos llevan asociada información, puede que ésta no sea de interés. Cada evento lleva asociada la información de la fecha y la hora en que el evento ocurre.

Como ya se había comentado con anterioridad, los eventos no tienen duración : o han ocurrido o no. La única forma de detectar si un evento ha ocurrido o no es considerar los efectos provocados por el mismo.

Al modelar una situación se consideran únicamente algunos de los eventos, al igual que al definir los tipos de objetos se consideran sólo aquellos que tienen interés para nosotros. Específicamente nos interesan sólo aquellos eventos que provocan cambios de estado en el modelo.

Hemos de tener en cuenta que los eventos no son objetos. Sin embargo, si un evento provoca un cambio de estado en el modelo, este conserva en realidad memoria acerca de la ocurrencia del mismo. A veces resultará interesante modelizar esta memoria como un tipo de objeto, creado como resultado del evento, y que posea el mismo nombre que el evento en sí. Por ejemplo, la ocurrencia de un evento de matrimonio entre dos personas puede representarse mediante un objeto de tipo matrimonio. Es importante comprender las diferencias entre el evento y la memoria del mismo (plasmada en un objeto).

Consideraremos ahora la forma en que se describen los eventos. La información asociada a los eventos se modeliza de dos formas :

•       mediante un nombre

•       mediante los parámetros del evento

Si consideramos el evento expresado por la siguiente frase :

"El tren de las 09 :45 hacia Soria sale de Atocha el día 17 de Junio de 1993"

Se asume que estamos interesados en el evento porque estamos construyendo un modelo que considera, entre otras cosas, estaciones y trenes. Claramente, este evento en concreto es uno de entre una familia de eventos similares, representando salidas de trenes. Una forma de describir este evento es la siguiente :

parte('09 :45 a Soria','Atocha','17-Junio-1993')

donde parte es el nombre del evento. Esta será una instancia del tipo de eventos

parte(Tren,Estación,Fecha)

Aquí, hemos considerado que la información de hora de salida y destino están incluidas dentro de las propiedades del tipo de objeto Tren. Como vemos, los tipos de eventos son una descripción genérica de una familia de posibles eventos, donde cada instancia del evento se asocia a parámetros que son objetos y valores conformes a los tipos de parámetros.

Alternativamente, podemos estar interesados en considerar la hora concreta en que el tren comienza a salir de la estación, en cuyo caso hemos de considerar un nuevo parámetro :

parte(Tren,Estación,Fecha,Hora)

Si no estamos interesados en el tren, el evento sería :

parte(Estación,Fecha,Hora)

Es decir, la forma en que se describen los eventos depende de la información que se necesite para reflejar los cambios de estado del modelo. Para los nombres de los eventos se usarán verbos en tiempo presente, ya que esto evita conflictos con otros nombres. Cada tipo de eventos ha de tener un nombre distinto.

Los parámetros de los eventos pueden ser tipos de objetos y tipos de valor. Si el parámetro es un tipo de objetos, significa que el evento porta con él la identidad de un objeto en particular. Los tipos de estado no pueden usarse como tipos de parámetros para los eventos.

Si el parámetro es de tipo valor, significa que el evento porta este valor con él.

A menudo la detección de un evento causará la creación, en el modelo, de una nueva instancia de algún tipo de objeto. En esta situación no tiene sentido que la identidad de este objeto aparezca como parámetro en el evento, ya que la nueva instancia, y por tanto su identidad, no existe hasta que el evento se detectó. En este caso lo lógico sería introducir como parámetro la identidad de un objeto ya existente que participará en una asociación con el nuevo objeto.

También es normal que los objetos utilicen un parámetro del evento para ver si están interesados en él o no. Por ejemplo, en el evento

enciende(s :Switch)

muestra que únicamente la instancia s de switch estará interesada en la ocurrencia de dicho evento.

Un parámetro de un evento también puede ser multi-valuado, siendo su tipo, por ejemplo :

conjunto de números

indicando que el parámetro representa una colección desordenada de números, de tamaño desconocido.

3.- Configuración inicial de objetos

Vamos a considerar la siguiente vista de tipos :

Si se quiere crear más de un objeto de tipo compañía, no aparece en el esquema ningún tipo que pueda actuar como tipo inicial : por lo que se ha de introducir alguno. Este tipo servirá para crear un objeto (conforme a dicho tipo) que iniciará el funcionamiento del sistema. Es decir, este objeto será la primera instancia de que dispongamos y a partir de la cual se vayan creando las demás. En nuestro caso, se decide introducir el tipo OficinadeRegistro. La instancia inicial de este tipo de objetos representa aquella oficina en que se registran todas las compañías que se consideren en nuestro modelo (todas las instancias de este tipo de objetos). Si hay necesidad de considerar varias oficinas de registro, debido por ejemplo a razones de localización geográfica, se ha de introducir un nuevo tipo inicial, por ejemplo aquel cuya única instancia representa el gobierno del país.

Una vez introducido el nuevo tipo, el modelo quedaría :

El tipo inicial se distingue por aparecer en una caja con el borde más grueso. En un modelo completo sólo habrá un tipo inicial. También es posible que no aparezca ninguno, al no haberse decidido aún cuál jugará ese papel. La selección del tipo inicial puede tener importantes consecuencias sobre el sistema final. Por ejemplo, debido a la restricción sobre el número de empresas en que puede trabajar un empleado ([1+]), una persona sin empleo no podrá accederse mediante navegación desde el tipo inicial. Si resulta necesario este acceso, se ha de introducir una asociación entre Persona y OficinadeRegistro, representando el conocimiento que esta tiene sobre las personas sin empleo.

Todas las asociaciones mantenidas con el tipo inicial presentarán una agregación en el extremo del mismo, ya que la persistencia del resto de instancias depende de la del tipo inicial.

La configuración inicial de objetos consta de una instancia simple del tipo inicial. En el caso del modelo anterior :

Una consecuencia de definir un tipo inicial de objetos es permitir que todos los eventos tengan al menos un parámetro de tipo objeto. En el ejemplo anterior podemos considerar el evento :

creaCompañía(OficinadeRegistro,Cadena)

que crea una nueva compañía. De esta forma se muestra la relación entre la compañía y la oficina de registro en que se inscribe.

Nunca es necesaria una configuración inicial de objetos que tenga más de una instancia del objeto inicial, ya que siempre se pueden definir eventos que provoquen la creación de nuevos objetos. Sin embargo habrá situaciones en que queramos que exista un conjunto de objetos como punto de partida.

4.- Definiendo los eventos

Una excelente forma de descubrir los eventos es considerar sistemáticamente los tipos de objetos y sus asociaciones en la vista de tipos. Para cada tipo hemos de considerar la forma en que se crean y destruyen sus instancias. Para cada asociación hemos de considerar :

•       cómo se crea una instancia

•       cómo se destruye una instancia

•       en el caso de que la asociación lleva a una ordenación, indicar los criterios para establecerla

Considerando el modelo anterior, se puede deducir la siguiente lista de eventos, necesarios para crear y eliminar objetos y para establecer y romper asociaciones entre objetos :

creaCompañía(OficinadeRegistro,nombre :Cadena)

crea una instancia del tipo compañía, relacionada con la oficina de registro (objeto inicial). Por tanto, crea una instancia y establece una asociación. La cadena pasada como parámetro será el nombre de la instancia de Compañía a crear. Considerar que OficinadeRegistro indica que el primer parámetro ha de ser una instancia de este tipo de objetos

creaDepartamento(Compañía,nombre :Cadena)

crea un departamento perteneciente a la Compañía pasada como primer parámetro, y que tendrá el nombre dado por el segundo. Crea una instancia y una asociación

destruyeCompañía(Compañía)

para la eliminación de una instancia del tipo de objetos Compañía

destruyeDepartamento(Departamento)

para la eliminación de una instancia del tipo de objetos Departamento

añadeEmpleado(Compañía,nombre :Cadena,salario :Número)

crea una instancia de Persona (cuyo nombre será el que aparece como segundo parámetro), y se establece una asociación entre la instancia de Compañía pasada como primer parámetro y la instancia de Persona creada. Esta asociación tendrá como valor de su propiedad salario el número pasado como tercer argumento

emplea(Compañía,Persona,salario :Número)

añade una relación de empleo entre dos instancias, una de tipo Compañía y otra de tipo Persona. Las diferencias entre esta y la anterior radica en que este evento no provoca la creación de ninguna instancia de tipo Persona

deja(Persona,Compañía)

este evento provoca la ruptura de una asociación entre una Persona y una Compañía. Debido a la limitación existente acerca del número de empleos que puede tener una persona ([1+]), si esta instancia de la asociación de empleo es la única que involucra a esta Persona, su desaparición conlleva la destrucción de la instancia de Persona

destina(Persona,Departamento)

establece una asociación entre una persona y un departamento

retira(Persona,Departamento)

elimina una asociación entre una persona y un departamento

Ha de evitarse la introducción de parámetros innecesarios. Así, en el evento

destina(Persona,Departamento,Compañía)

resulta redundante incluir Compañía, ya que el departamento está asociado, de forma unívoca, con ella.

El estudio de los tipos de objetos y de las asociaciones establecidas entre ellos puede no ser suficiente para la obtención de todos los eventos dentro de nuestro sistema. Hay eventos que estarán asociados, únicamente, con cambios de estado en los objetos (sin que produzcan ni creación o destrucción de instancias ni establezan asociaciones entre ellas). Estos eventos se ponen de manifiesto al realizar un análisis detallado de los tipos de objetos, por separado. Por ejemplo, todas las propiedades no constantes de un objeto han de poder cambiar como resultado de al menos un evento.

En el caso anterior, se necesitará un evento que modifique la propiedad salario de la asociación entre Persona y Compañía.

5.- Validación de eventos

Vamos a trabajar con una instancia del modelo considerado, cuyo estado actual viene determinado por el siguiente diagrama :

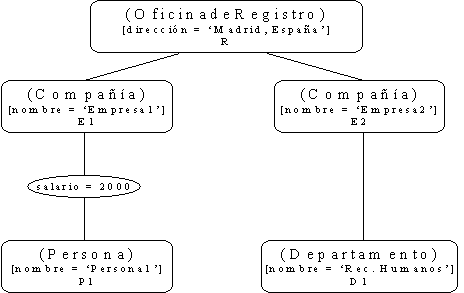
Se ha proporcionado nombre simbólico (R, E1, E2, ..) a los objetos, para que puedan ser referenciados en los eventos.

Los eventos válidos, en cualquier situación, serán aquellos que pueden aparecer. Los eventos pueden ser inválidos por alguna de las siguientes razones :

•       parámetros erróneos : si aparece alguno de ellos perteneciente a un tipo distinto del especificado, o si se referencia algún objeto cuya identidad es desconocida. Por ejemplo, en el caso anterior :

creaDepartamento(E1,20)

es erróneo, ya que como segundo argumento se espera una cadena y no un número. El evento

creaDepartamento(E3,"Recursos Humanos")

tampoco es válido en el instante considerado, ya que aparece una compañía cuya identidad no se conoce.

•       parámetros inválidos : si los parámetros, en conjunto, violan las restricciones del modelo. Por ejemplo :

añadeEmpleado(E1,'Pedro' ,-20)

viola la restricción sobre que el salario ha de ser mayor que 0. Un ejemplo más sutil es

destina(P1,D1)

y resulta incorrecto ya que la persona P1 no trabaja para la compañía que posee el departamento D1.

•       modelo en estado incorrecto : cuando ocurren eventos que afectan a tipos de estados no permitidos. Por ejemplo consideraremos la siguiente situación :

En este modelo tendremos que considerar la existencia de dos eventos, que permitan modificar el estado de la empresa

hazPública(Compañía)

hazPrivada(Compañía)

Una empresa que ya sea pública no podrá recibir un evento hazPública. Igual ocurrirá con una empresa Privada y el evento correspondiente.

Se observa, por tanto, que para conocer si un evento determinado puede ocurrir, necesitamos conocer el estado actual de los objetos sobre los que actúan los eventos.

6.- Precondiciones

Para cada tipo de evento se puede escribir, en lenguaje natural, las condiciones que se deben de cumplir para que ocurra. Es conveniente hacerlo y nos servirá posteriormente como punto de partida para la especificación formal de sus precondiciones.

Como se ha visto al contemplar el tipo de situaciones que invalidaban la validez de un evento, podían deberse a dos tipos de situaciones generales : relacionadas con los parámetros y relacionadas con el modelo. En estas dos categorías se engloban también las precondiciones.

Recordando los eventos definidos con anterioridad, las precondiciones se expresaban de la siguiente manera :

añadeEmpleado(Compañía,nombre :Cadena,salario :Número)

El salario ha de ser mayor que 0

destina(p :Persona,d :Departamento)

La persona p ha de trabajar en la empresa a la que pertenece el departamento d

hazPública(c :Compañía)

La compañía c no puede ser pública

El efecto de las precondiciones es impedir que ocurra un evento que no las cumpla.

7.- Consecuencias

La consecuencia de un evento será, normalmente, modificar de alguna manera el estado del modelo.

Las consecuencias de un evento pueden especificarse de forma informal. Como se dijo con anterioridad, se tratará de un buen punto de partida para el momento en que se necesite su especificación formal.

Para los eventos considerados con anterioridad, las consecuencias pueden expresarse de la siguiente manera :

añadeEmpleado(c :Compañía, n:Cadena,s :Número)

Se crea un nuevo objeto de tipo Persona, con nombre n, trabajando para la Compañía c y con salario s

destina(p :Persona,d :Departamento)

La persona p será asociada con el departamento d

hazPública(c :Compañía)

La compañía c pasa a estar en estado pública

8.-Tablas de eventos

Es bastante conveniente documentar todos los tipos de eventos que se producen en un sistema. Para ello se utiliza una tabla de 5 columnas, como la que se muestra a continuación :

Nombre	Parámetros tipos de objetos	Parámetros de valor	Precondiciones	Consecuencias	Comentarios
El nombre del tipo de evento	Tipos de objetos que intervienen como parámetros	Tipos de valores que actúan como valores	Descripción de condiciones que han de ocurrir para que suceda el evento	Cambios producidos en el modelo por la ocurrencia del evento	Cualquier tipo de comentario

9.-Escenarios de eventos

Como ya se ha comentado, no todos los eventos pueden ocurrir en cualquier instante, si no sólo en un determinado orden. Se pueden especificar secuencias de estos eventos, denominadas escenarios de eventos.

En esencia, un escenario de eventos es una lista de instancias de eventos, donde cada instancia de eventos viene especificada por su tipo y los valores de sus parámetros.

En muchos casos los parámetros de los eventos serán identidades de objetos, que deberemos de representar simbólicamente.

Imaginemos que hemos creado una instancia de una oficina de registro, en el modelo anteriormente considerado. Esta instancia del tipo de objeto Oficina de Registro, se conoce simbólicamente como R.

Consideremos la siguiente secuencia de eventos :

creaCompañía(R,"Producciones Empresa1, S.A")

creaCompañía(R,"Alimentación Pepe")

Esta secuencia de eventos provoca la creación de dos compañías. El estado del modelo, en este punto, puede representarse mediante el siguiente diagrama :

A partir de este punto, podemos continuar, por ejemplo, añadiendo un empleado a la Compañía llamada simbólicamente C1.

AñadeEmpleado(C1,"Juan",2000)

Esto deja al modelo en el siguiente estado :

Mediante la combinación de la lista de eventos con los diagramas de objetos mostrados, se pueden describir escenarios bastante tan complejos como se deseen.

10.-Estados

Los eventos sólo pueden producirse en secuencias determinadas. Estas secuencias están limitadas de acuerdo a la realidad de la situación bajo estudio. Por ejemplo, un indicador luminoso presenta dos eventos asociados : enciende y apaga.

Si queremos conocer cuál de estos dos eventos ocurrirá a continuación, hemos de considerar si el indicador está actualmente encendido o apagado. Si está apagado, la única posible secuencia de eventos será : enciende, apaga, enciende, ....

Para describir esta situación se puede presentar el siguiente esquema :

En principio, cada conjunto de valores de las propiedades de un objeto define o representa un estado diferente del mismo. Esto significa un número infinito de ellos, ya que, por ejemplo, dentro del rango de enteros tenemos un conjunto infinito de posibles valores. En realidad sólo se consideran aquellos estados que representan cambios significativos en el modelo.

Por ejemplo, consideremos un sistema de embotellado, donde las botellas finalizan siendo tapadas. Las botellas pueden representarse por el siguiente tipo de objetos :

Resulta obvio que este tipo de objetos puede presentar, en sus propiedades, un conjunto infinito de valores, pero el ciclo de vida de sus instancias puede recogerse en el siguiente esquema :

El estado Vacía, en la figura anterior, representa un conjunto entero de valores de propiedades donde contenido < capacidad. El diagrama anterior proporciona una definición precisa de las posibles secuencias de eventos. La única será : rellena, tapa.

11.-Diagramas de estados

Los diagramas vistos hasta ahora, como el anterior, son ejemplo de máquinas de estado finitas.

Nosotros consideraremos un formalismo más completo : la notación de diagramas de estado de Harel. Este formalismo soporta estados anidados y máquinas ortogonales, como veremos a continuación.

Estos diagramas proporcionarán formas de describir la forma en que un objeto cambia entre sus posibles estados. En realidad muestran información sobre todo lo siguiente :

•       lista de eventos de interés para un tipo de objetos

•       máquina de estados finita

•       detalles sobre la creación de objetos

•       limitaciones sobre la validez de eventos

•       descripción de secuencias de eventos

Consideremos los elementos que componen un diagrama de estado. Cada estado, incluido aquel que representa el diagrama entero, se representa mediante un rectángulo redondeado, denominada caja de estado. Una caja de estado se divide en tres secciones, como se aprecia en la figura que sigue :

Las secciones que no se usen se omiten. El nombre del estado aparece en la parte superior, separado del resto de contenidos por una línea horizontal. El diagrama entero es un estado, cuyo nombre será el del nombre del tipo relacionado. Los nombres de estado han de ser únicos dentro de un diagrama.

En la figura siguiente aparece un diagrama para una botella, en la situación comentada con anterioridad.

La sección para el texto contiene la lista de eventos de interés para el tipo de objetos considerado. Cada uno de estos eventos proporciona el prototipo completo de un tipo de eventos, incluyendo los nombres formales para cada parámetro. Cuando los eventos aparecen en el diagrama, sólo se muestran aquellos parámetros necesarios para describir la transición. En este ejemplo no se ha considerado ninguno, al ser las transiciones suficientemente claras sin más especificación.

Veamos la forma en que se interpretará este diagrama. Se muestran tres estados (Vacía, Llena y Cerrada), que por convención, comenzarán con mayúscula. La flecha con un círculo negro muestra el estado inicial (Vacía). Es decir, cuando se crea una nueva instancia de este tipo de objetos, se encontrará en este estado. Como se puede apreciar las botellas sólo están interesadas en dos tipos de eventos : rellena y tapa. Cada uno de los eventos lleva como parámetro la instancia de un objeto de tipo botella. La transición entre estados se produce cuando tiene lugar el evento indicado en la misma.

Para validar el conjunto de eventos consideraremos que los eventos pueden ocurrir si aparecen en una situación en que pueden "disparar" una transición.

A una secuencia de eventos que puede ocurrir se denomina secuencia válida de eventos.

Añadiremos al diagrama anterior dos nuevos eventos : el evento rompe ocurre cuando la botella se rompe mientras está siendo rellenada o en espera de ser rellenadas. El evento reset ocurre cuando una botella que está siendo rellenada, o en espera de serlo, se vacía (si es necesario) y retorna al comienzo de la línea de producción. Las transiciones que comienzan y terminan en el mismo estado se denominan auto-transiciones.

Para reducir el conjunto de transiciones, se puede usar el concepto de estados anidados. El diagrama resultante sería :

Se ha introducido un nuevo estado, llamado EnProceso, que engloba los estados Vacía y Llena. Una transición que se aplica al estado EnProceso se aplica también a cada uno de los estados anidados. Ahora necesitamos dos flechas para indicar los estados iniciales : uno para el más exterior (EnProceso) y otro para los estados anidados en él (en este caso será para Vacía). Si tenemos una transición cuyo destino es EnProceso, la flecha de estado inicial nos diría cuál de los estados iniciales sería el que desempeñaría el objeto sobre el que se aplica. Lo que tenemos realmente es dos máquinas de estado : una con los estados EnProceso, Rota y Cerrada, y otra con los estados Vacía y Llena.

Cualquier estado puede contener estados anidados, y la anidación se puede producir en tantos niveles como deseemos.

En la figura que aparece a continuación se ha introducido un nuevo estado : Gotea. Además se añade una transición desde Llena hasta este nuevo estado. Ahora, como se ve, existen dos transiciones posibles desde el estado Llena, con el evento rompe : una directa y otra en virtud de su anidamiento en el estado EnProceso. Esto está permitido, y en estas situaciones la transición más interna sería la que se activara.

Debe existir una correspondencia exacta entre los estados en el diagrama de estados y los tipos de estado mostrados en la vista de tipos. Los estados anidados aparecerán, en la vista de tipos, como subtipos del estado que los encierra. Es decir, correspondiente al diagrama anterior aparecerá el siguiente modelo para el tipo de objetos Botella.

Aunque esta correspondencia existe, no es necesario que aparezcan todos los estados en la vista de tipos. Sólo será necesario considerar aquellos aquellos que pongan de manifiesto dependencias de propiedades o asociaciones.

Si consideramos ahora las precondiciones reseñadas frente al evento

añadeEmpleado(c:Compañía,nombre:Cadena,salario:Número)

(el salario debe ser mayor que 0), estas deben de aparecer en la lista de eventos, tras la descripción del tipo de eventos, encerrada entre corchetes. Es decir, en la lista de eventos del diagrama de estados de Compañía aparecerá :

añadeEmpleado(c:Compañía,nombre:Cadena,salario:Número) [salario > 0]

De forma análoga, en el diagrama de estados de Persona aparecerá, en su lista de eventos, el siguiente

destina(p :Persona,d :Departamento) [d.compañía empleador]

12.-Guardas

Vamos a considerar ahora un modelo simplificado sobre el ejemplo de la planta de llenado de botellas, donde nos centramos exclusivamente en el llenado de las mismas. Quizás el llenado de una botella pueda considerarse como una serie de inyecciones de líquido en la botella. El evento rellena se sustituye por el evento inyecta, que presenta un parámetro numérico que indica la cantidad de líquido inyectada. Se puede definir, de forma general, el número de eventos necesarios para rellenar una botella, como se muestra a continuación :

Las transiciones presentan lo que se denominan guardas. Se trata de condiciones lógicas que deben de cumplirse para que se pueda producir la transición.

Mediante la introducción de guardas se puede considerar la situación en que tengamos varias transiciones para un mismo evento, a partir del mismo estado.

En el ejemplo anterior se observa que la transición a Llena se producirá en el momento en que el contenido de la botella alcance la capacidad máxima. Mientras esto no ocurra, la aplicación de un evento inyecta no provoca cambios de estado ( y se permanece en el estado Vacía). Considerar las diferencias entre precondiciones y guardas. Las precondiciones se refieren a la validez de los parámetros (para que sean válidos han de cumplirse). Las guardas están relacionadas con condiciones de aplicación (una vez validados).

Las expresiones lógicas para las guardas pueden utilizar los nombres bajo el ámbito del tipo correspondiente, más todos los correspondientes a los tipos de estado.

Un diagrama de estados en que las guardas permitan que más de una transición pueda dispararse ante un determinado evento está mas especificada.

En el ejemplo considerado, se aprecia que el or entre las guardas conduce siempre a TRUE, por lo que siempre ocurrirá un evento. Esto no siempre ha de ser así. Imaginemos que la transición entre los estados Vacía y Llena se hace a través del evento inyecta, con la siguiente guarda :

inyecta(n) [contenido + n > capacidad]

En este caso, en el momento en que contenido + n = capacidad , no se cumplirá ninguna de las dos transiciones. En este caso podemos deducir que ningún evento de inyección rellenará exactamente la botella. En esta situación la guarda actúa también como precondición, ya que no sólo especifican el cambio de estado correcto, si no también las condiciones bajo las que puede existir un evento inyecta.

En aquellas situaciones en que el or entre las guardas de los eventos que parten de un estado sea TRUE, delimitan caminos sobre el diagrama de estados (qué transición seguir). En aquellas circunstancias en que esto no sea así, las guardas actuarán también como precondiciones.

Como se aprecia en este tipo de diagramas, el diagrama de estados completo representa un estado del tipo de objeto correspondiente que engloba a todos los demás. Esto nos permite usarlos para simplificar los diagramas, reduciendo así el número de transiciones.

Un evento vacía se introduce, que conduce a la botella, desde cualquier estado al de Vacía. Presentado el evento de esta manera, nos evitamos dibujar dos transiciones diferentes : una desde el estado Llena y otra desde Vacía.

Hay otra forma de dibujar el anterior diagrama de estados. Se basa en la idea de permitir eventos. Indicando, como se verá a continuación, que deseamos permitir un evento, se muestra que este evento será aceptable en cualquier estado : en algunas situaciones provocarán una transición y en otras no. Permitir un evento es equivalente a :

•       incluir una auto-transición, sin guardas, para todos aquellos estados en los que no exista ya una transición para este evento.

•       incluir una auto-transición, con guarda, en aquellos estados en que ya existan transiciones para dicho evento, con la guarda recogiendo la negación de la condición lógica (o su or si hay varias) de la(s) guarda(s) existente(s).

Al permitir el evento vacía, se establece una auto-transición, con este evento, en el estado Vacía, por no existir en él ninguna otra transición para el mismo. Pero el estado Llena si presenta una transición con este evento hasta Vacía. Por lo explicado anteriormente, tendríamos que introducir para este estado una nueva autotransición para este evento. Como guarda se pondría la negación de la condición lógica de las guardas ya existentes (o su or si hubiese varias). Como la transición ya existente no presenta guarda alguna, es equivalente a una condición lógica de TRUE, por lo que la negación lógica equivale a FALSE. Es decir, introduciríamos una autotransición que nunca se cumpliría, por lo que no resulta necesario hacerlo.

Este permiso puede extenderse a todos los eventos considerados. Una de estas sentencias de permiso tendrá efecto sobre el estado en que se define y sobre todos sus estados anidados.

Esto no supone, en absoluto, olvidar las precondiciones de los eventos.

Esto supone que los eventos permitidos, si cumplen las precondiciones que les afecten (si las hubiera), podrán ocurrir en cualquier instante sobre el diagrama de estados considerado, aunque en realidad no produzcan ninguna transición de estados.

Habiendo considerado este concepto, se puede definir de mejor modo la validez de una secuencia de eventos : cada evento de una secuencia válida de eventos, que aparecerá en la lista de eventos del diagrama de estado, ha de satisfacer las precondiciones (si las hay) y debe provocar una transición o bien estar permitido. Una secuencia de eventos será válida para el modelo completo, si y sólo si es válida para todos los diagramas de estado del modelo.

Vamos a considerar de nuevo el siguiente diagrama de estados :

Para completar la descripción que presenta hemos de indicar que la propiedad contenido presenta un nuevo valor tras la ocurrencia de un evento inyecta. Esto se hace mediante la inclusión de postcondiciones : se trata de expresiones lógicas que serán ciertas una vez sucedido el evento. Estas postcondiciones formalizan el concepto de consecuencia visto con anterioridad. El conjunto de nombres que se pueden usar en su especificación es el mismo que el indicado para el caso de las guardas.

Ya que habrá muchas situaciones en que se desee hacer mención a los valores previos y posterior de una propiedad, se añade la comilla (�) a la propiedad, indicando así que se trata del valor de la propiedad tras la ocurrencia del evento.

Veamos la forma en que se añadirían postcondiciones al diagrama anterior :

Vemos que las precondiciones aparecen tras las guardas, separadas de ellas por el carácter �/', encerradas entre corchetes.

Si, como ocurre en el caso anterior, son las mismas para todas las transiciones guiadas por un evento, se especificarán en la propia descripción del evento :

Como regla general, las postcondiciones no producirán cambios en el estado de más objeto que en self (el objeto en el que se origina la transición : en nuestra caso será una botella). Si un evento provoca cambios en el estado de varios objetos, ha de especificarse de forma separada para cada uno de sus tipos de objetos correspondientes, sobre sus diagramas de estado correspondientes.

13.-Operaciones de creación

Los objetos (sus instancias) son dinámicamente creados y destruidos durante el tiempo de vida de una determinada situación. En el diseño de las vistas de estado, tema que nos ocupa, se ha de reflejar no sólo la manera en que los eventos producen cambios en los estados de los objetos, si no también la forma en que se crean y se destruyen.

En el momento de creación de una nueva instancia de un tipo de objetos, ésta tomará propiedades y asociaciones a partir de información ya presente en el modelo o a partir de la aportada por el propio evento. Hemos de ver la forma en que esta información se hace visible para la nueva instancia en juego. Se hará a través de las operaciones de creación.

La creación de un objeto en el modelo, descrito de forma simple, invoca a una operación de creación. Un objeto de un tipo determinado no podrá crearse si el tipo al que pertenece no ha definido una operación de creación (en C++ estaríamos hablando del constructor de la clase). La operación de creación más simple será aquella que no involucra parámetro alguno. En algunas situaciones se hará necesaria la existencia de operaciones de creación más sofisticadas. Esto es perfectamente posible y lo normal será que para cada tipo se disponga de un conjunto de operaciones de creación distintas, diferenciadas por el conjunto de parámetros que requieren. La información pasada como parámetro será la que se haga disponible para el nuevo objeto. Las operaciones de creación, por otra parte, no tienen nombre y se describen únicamente por el conjunto de los parámetros que manejan.

Se puede asociar una postcondición a la flecha de estado inicial, indicando los valores iniciales usados por las propiedades (y asociaciones) de los objetos creados.

En la figura que sigue se muestra que se ha definido una operación de creación para objetos del tipo considerado, que aceptan un valor numérico como parámetro, que se usará para especificar su propiedad de capacidad.

También especifica un valor inicial de 0 para el contenido.

Como se aprecia, la operación de creación aparece en la parte más externa de la sección de texto del diagrama de estado.

Claramente las propiedades y nombres de asociaciones usados en las postcondiciones de las operaciones de creación han de ir marcados con el carácter (�), ya que el objeto en sí no existe hasta finalizar la creación del objeto.

Como se hacía en el caso de las postcondiciones, pueden especificarse en la sección de texto. En la figura siguiente se muestra el caso en que se definen dos operaciones de creación distintas, cada una con un conjunto distinto de parámetros :

Una posible alternativa al diagrama anterior sería presentar dos flechas distintas para el estado inicial, etiquetadas con los parámetros adecuados para cada una de las operaciones de creación. Esto se hace solamente en aquellas situaciones en que diferentes operaciones de creación dejen al nodo en estados diferentes. Se puede incluso incluir guardas sobre las flechas de estado inicial, que permitirán seleccionar un estado de inicio dependiendo de los parámetros de creación. Estas guardas sólo pueden hacer referencia a los nombres de los parámetros formales de la operación de creación, nunca al estado de los objetos (ya que el objeto, en realidad, aún no ha sido creado).

Un ejemplo de esto aparece en el siguiente diagrama :

Recordar aquí que no se pueden asociar ni guardas ni postcondiciones a aquellas flechas de estado inicial que aparecen en diagramas anidados, para mostrar cuál es el estado por defecto.

Aunque la definición de las operaciones de creación corresponde a los diagramas de estado, si se quiere, se pueden incluir también en la vista de tipos. No hace falta proporcionar nombres formales para los parámetros : sólo los tipos.

Las postcondiciones también pueden usarse para mostrar que la consecuencia de un evento es la creación de uno o más objetos nuevos. Para verlo consideraremos la siguiente vista de tipos :

Consideremos que existe un evento del tipo :

hazBotella(m : Fabricante, c : número)

que ocurre cuando se crea una nueva botella. La postcondición de este evento es que tras él existe una nueva botella, con capacidad c.

Esto se puede expresar de la forma :

donde se aprecia cómo se invoca la operación de creación.

Para cualquier tipo de objetos X la expresión

new X

conducirá a la creación de una nueva instancia del tipo X, invocando a la operación de creación que presente sin parámetros. Si se especifican parámetros, se seleccionará aquella operación de creación adecuada.

Si en la figura anterior optamos por pasar la postcondición a la sección textual, junto al evento correspondiente. Esto dejaría la sección principal "degenerada", con un estado simple con una sola autotransición sin guardas. Estas secciones principales degeneradas pueden eliminarse. La ausencia de sección principal, junto con una lista de eventos, implica la presencia de un único estado, con autotransiciones sin guardas para cada evento de la lista.

14.-Creación de asociaciones

En la figura anterior no se muestra información acerca de la asociación entre el objeto de tipo botella y la instancia de Fabricante correspondiente a su productor.

Esto se pone de manifiesto en la figura siguiente :

En la expresión de post-condición, producto hace alusión al conjunto de botellas obtenidas por navegación de la asociación de producción entre Botella y Fabricante, es decir, el conjunto de botellas fabricadas por el fabricante considerado antes del evento ; producto' se refiere al mismo conjunto de botellas, pero tras la ocurrencia del evento. Es claro que el nuevo conjunto será igual al anterior más la nueva instancia de botella creada tras que ocurra el evento hazBotella. Con definir la asociación en un sentido basta, ya que una vez establecida podrá ser navegada en ambas direcciones.

15.-Finalización

Algunos eventos producirán la destrucción de algunas de las instancias presentes. Extendiendo nuestro diagrama de estados anterior para el tipo de botellas, podría ser interesante modelizar el hecho de que las instancias dejan de ser de interés para el sistema en el momento en que son empaquetadas.

Cuando un objeto se destruye, deja de ser conocido en la situación y cualquier asociación que mantuviese se destruye también.