HISTORIA

 

Aunque hoy nos es muy familiar el concepto de número, éste fue elaborado muy lentamente a través de los tiempos. Incluso en tiempos recientes, tribus que mantenían normas de vida muy primitivas tenían los conceptos numéricos muy atrasados. Por ejemplo, se dan casos en los que no existía nombre para cantidades mayores que tres; en otros, para números un poco mayores se utilizaban términos similares a "muchos" o "incontables".

 

Si retrocedemos al tiempo, de las cuatro grandes civilizaciones del mundo occidental antiguo (  Babilonia,  Egipto,  Grecia y  Roma), veremos que babilonios y griegos desarrollaron elevados conocimientos de matemáticas.

 

Para poder realizar importantes obras agrícolas y arquitectónicas, los babilonios tuvieron que desarrollar, hacia el siglo XXII a. de C., un sistema de numeración útil.

 

Se sabe que su sistema de numeración era de base 60 (a diferencia del actual, que es de base 10); es decir, dividían la unidad en 60 partes (de forma similar a como dividimos una hora en 60 minutos). Los sumerios también utilizaban este sistema de numeración, y realizaban complicados cálculos aritméticos.

 

Aunque los  egipcios no hicieron aportaciones tan significativas como los griegos al desarrollo de los números, se ha encontrado un interesante documento, en el cual se demuestra que ya manejaban algunas fracciones sencillas. Este documento se denomina el Papiro de Rhind. Fue escrito bajo el reinado del rey Ekenenre Apopi, hacia el 1600 a. de C., y, al parecer, es una transcripción de un escrito más antiguo, que se remontaría al reinado de Amenemhat o Amenemes III (XII dinastía, 1850-1800 a. de J. C.). En este papiro se observan unas reglas para realizar sumas y restas de fracciones.

 

Cuando se debía realizar una repartición exacta, no se presentaban problemas de cálculo; sin embargo, si había que dividir 42 panes entre 10 personas, la operación se complicaba. En estos casos, los babilonios utilizaban el número decimal (4,2), mientras que los egipcios, con un sistema de numeración más primitivo, necesitaban de las fracciones para expresar estas divisiones no exactas. Conocían las fracciones de numerador 1 y de denominador 2, 3, 4 , etc., además de las fracciones 2 / 3 y 3 / 4. En el papiro de Rhind se propone un método de cálculo (bastante pesado) que permite dividir 2 entre 19 de la siguiente manera: 

 

Los  chinos también conocían las fracciones, y sabían reducir a común denominador. Llamaban "hijo"  al numerador, y "madre" al denominador.

 

Pero, entre todos los pueblos de la antigüedad, fueron los  griegos los que realizaron las aportaciones más valiosas al  desarrollo del concepto de número. La escuela pitagórica (siglo V a. de C.) descubrió que sólo con los números naturales y las fracciones no pueden realizarse todas las medidas posibles. Existían pares de segmentos, como la diagonal y el lado de un pentágono regular, o la diagonal y el lado de un cuadrado, cuyo cociente de longitudes no es una fracción. Creyeron que el caos entraba en su mundo ordenado, y llamaron a tal razón "alogos" o irracional.

 

Posteriormente se desarrolló el concepto de número negativo. Fueron los chinos, quienes en el siglo III a. de C. emplearon las varas de contar, un conjunto de barras pintadas de rojo para los números positivos, y de negro para los negativos. Un siglo después, aparecen por vez primera reglas para operar con los números negativos; sin embargo, no eran aceptados como soluciones de los problemas.

 

Siglos después, hacia el año 500, en la  India se plasmaron los orígenes de nuestro sistema de numeración. El principio de posición (valor relativo de las cifras), las nueve cifras y el cero aparecen en las obras del matemático indio Brahmagupta. Durante esta época, los matemáticos indios también aceptaron las soluciones negativas de las ecuaciones, al tiempo que admitían como números las raíces de otros números que no podían ser expresados mediante números racionales.

 

En el año 772, una embajada india llevó hasta Bagdad los libros en que se recogían estos conocimientos. Gracias a este hecho, en la primera mitad del siglo IX se recopilaron los nuevos métodos matemáticos en un tratado de Al-Khuwarizmi, que en el siglo siguiente se difundieron lentamente por Occidente.

 

La  civilización musulmana llevó estos conocimientos a Sicilia y a España, y los mercaderes árabes e italianos los adoptaron, satisfechos de no tener que llevar consigo el incómodo ábaco. Fue el mercader Leonardo Pisano quien, después de haber aprendido aquel arte de los árabes en sus viajes comerciales por Argelia, Sicilia y Oriente, reunió todos los conocimientos de aritmética y álgebra de su tiempo en una obra llamada Liber Abaci (1202), que difundió por Europa la numeración india.

 

Hasta entonces, en  Europa se habían evitado los números negativos; pero en el siglo XIII, el matemático italiano Fibonacci, en un problema referente al dinero, que no tiene solución positiva, observó su necesidad. Durante el siglo XIV, los números negativos eran denominados numeri absurdi. Se debió esperar hasta el siglo XV, para que el francés Chaquet expresara por primera vez un número negativo aislado en la ecuación

 

4x = -2

 

Durante el  siglo XVI, se popularizó el uso de la barra horizontal para separar los términos de una fracción, nomenclatura de origen árabe. Pero, aunque algunos problemas se solucionaban, surgían otros. Al intentar resolver ecuaciones de segundo grado como

 

   

x2 - 2x + 5 = O

 

y otras de grado mayor, empezaron a encontrarse expresiones, como  la raíz cuadrada de -16, que no se sabían interpretar. Aun sin entenderlas, algunos comenzaron a manipularlas con las mismas reglas que utilizaban para los números que conocian. Fue Cardano, durante este mismo siglo, quien propuso un nuevo tipo de números, que denominó ficticios, como solución a las raíces cuadradas de números negativos.

 

El problema de los números irracionales no se resolvió por completo hasta el Siglo XVII, cuando Fermat, matemático francés que puede ser considerado el padre de la moderna teoría de números, demostró que expresiones como raíz cuadrada de 3 no eran números racionales.

 

Sólo quedaba por resolver el problema de las raíces negativas; y esto ocurrió en 1777, cuando Euler dio a la raíz cuadrada de  -1 el nombre de i ( imaginario). En 1799, Gauss acabó de resolver el problema al demostrar que las soluciones de cualquier ecuación algebraica, fuera cual fuese su grado, pertenecía a un conjunto de números que él llamó complejos, a los que consideró compuestos de un número  "ordinario" (hoy lo llamamos número real), más un múltiplo de la raíz cuadrada de  -1, llamado unidad imaginaria.

 

Como ha podido comprobarse, para llegar a conceptos que hoy nos parecen sencillos y lógicos, han tenido que pasar muchos siglos y muchas culturas, cada uno de los cuales ha hecho sus aportaciones al conocimiento de los números.

 

  Numeraciones de otras civilizaciones.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

LOS NUMEROS:  e , PI , i

 

Sin duda, los tres números más famosos y que más atracción han despertado son: p, e, y i

 

* El número p se ha estudiado durante siglos, y no es más que la razón entre la longitud de la circunferencia y su diámetro:

 

 

 

* El número e, más tardío, es el límite de la sucesión de término general.

 

 
es decir,

 

* La unidad imaginaria i, se introdujo para poder dar solución a la ecuación  x2 + 1 = 0

 

 
A pesar de tener un origen tan dispar, los tres números se relacionan mediante una expresión extremadamente sencilla:

 

 

Esta igualdad se deduce de la expresión exponencial de los números complejos:

 

 

 

 

 

 

LA UNIDAD IMAGINARIA

 

Llamamos unidad imaginaria al número Ö- 1, que se representa con el símbolo i

 

De esta manera, tenemos que:  i = Ö- 1  o    i2 = - 1

 

Con la unidad imaginaria i se pueden realizar operaciones ( suma, resta, multiplicación, etc.) de manera similar a la de la familiar X de los polinomios. Con una sola excepción:  i2 = -1

 

Se admiten, por tanto, manipulaciones como las que siguen:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

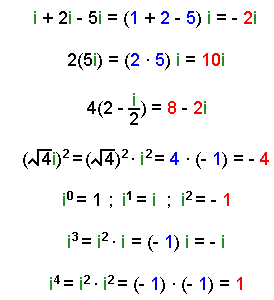
NUMEROS COMPLEJOS

 

Se llama número complejo a una expresión de la forma a + bi, donde a y b son números reales.

 

El número a se llama parte real. El número b se llama parte imaginaria. 

 

5 + 3i  (5 es la parte real, 3 la parte imaginaria)

-7 + 4i  (- 7 es la parte real, 4 la parte imaginaria)

-1 -  i    (- 1 es la parte real, - 1 la parte imaginaria)

 

Son casos especiales los complejos que tienen la parte real o imaginaria nula:

 

Si b = 0, el número complejo se reduce a un número real, ya que a + 0i = a. 

 

Si a = 0, el número complejo se reduce a bi; se dice que es un número imaginario puro.

 

Si a = 0 y b = 0, resulta el número complejo 0 + 0i, que se llama número complejo cero, y se escribe 0.

 

Dos números complejos son iguales si lo son las partes reales e imaginarias, respectivamente.

 

Se llama conjugado de z = a + bi al número complejo z definido por z = a - bi.

 

 

 

 

 

 

 

 

LOS REALES COMO SUBCONJUNTO DE LOS COMPLEJOS

 

  Al conjunto de los números complejos lo denotaremos C.

 

Todo número real se puede considerar como un número complejo con parte imaginaria cero:

 

a = a + 0 i 

 

Por tanto el conjunto de los números reales es un subconjunto de los complejos:

 

 

SUMA Y RESTA

 

 

 

Queremos sumar los números complejos 3 - 2i  y  5 + 6i:

 

(3 - 2i) + (5 + 6i) = 3 + 5 - 2i + 6i = 8 + 4i

 

Análogamente procederemos para restar el número complejo 4 - 7i de otro complejo 6 - 5i:

 

(6 - 5i) - (4 + 7i) = 6 - 4 - 5i - 7i = 2 - 12i

 

Partiendo de estos ejemplos, se puede generalizar y decir que se suma (o se resta) parte real con parte real, y parte imaginaria con parte imaginaria:

 

 

MULTIPLICACION

 

Para multiplicar complejos, se aplica la propiedad distributiva como si se tratara de números reales; debe tenerse en cuenta que :  i = Ö-1 ,  i2 = -1

 

( 3 + 4 i ) · ( 2 - 5 i ) = 26 - 7 i 

 

En general, se tiene que:

 

( 3 + 4 i ) · ( 2 - 5 i ) = [ 3 · 2 - 4 · (- 5) ] + [ 3 · (- 5) + 4 · 2 ] i = 26 - 7 i

 

Observación:

 

El producto de un número complejo por su conjugado, es un número real:

 

( a + bi ) · ( a - bi ) = a2 + b2  

 

( 2 + 3 i ) · ( 2 - 3 i ) = 4 + 6 i - 6 i - 9 i2 = 4 + 9 = 13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

DIVISION

 

Para dividir el número complejo 5 + 15i entre el número complejo 2 + i: 

 

 

multiplicaremos numerador y denominador por el conjugado del denominador; así, el resultado no se altera y, además, el divisor pasa a ser un número real:

 

 

En general:

 

INVERSO DE UN NUMERO COMPLEJO

 

Recuerda  que  el  inverso  de  un  número   N   es  otro  número   N'   tal  que  su  producto de 1:      N · N' = 1

 

El inverso del número complejo a + bi es:

 

     
ya que:

 

 

 

POTENCIACION

 

 

Para calcular (a + bi)n, podemos aplicar la propiedad distributiva y operar como en las expresiones algebraicas:

 

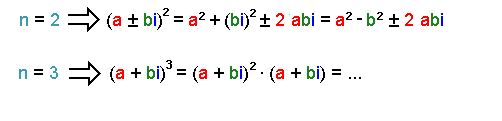
Si las potencias son superiores a 3, es conveniente utilizar la expresión del binomio de Newton

 

 

Desarrollando por el binomio de Newton la potencia (2 + 3i)4 y operando, obtenemos como resultado - 119 - 120 i 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

COMPLEJOS: PROPIEDADES DE LAS OPERACIONES

 

La adición  y la multiplicación  tienen las mismas propiedades que cuando de números reales se trata. Las enunciamos sin  demostrarlas, tarea que dejamos al lector.

Conmutativas:

 

( a + b i ) + ( c + d i ) = ( c + d i ) + ( a + b i )

 

( a + b i ) · ( c + d i ) = ( c + d i ) · ( a + b i )

 

Asociativas:

 

[ ( a + b i ) + ( c + d i ) ] + ( e + f i ) = ( a + b i ) + [ ( c + d i ) + ( e + f i ) ]

 

[ ( a + b i ) · ( c + d i ) ] · ( e + f i ) = ( a + b i ) · [ ( c + d i ) · ( e + f i ) ]

 

El elemento neutro de la suma es 0 = 0 + 0 i

 

El elemento neutro de la multiplicación es 1 = 1 + 0 i

 

El elemento opuesto de  a + b i  es  - a - b i

 

El elemento inverso de  a + b i  es  ( a - b i ) / ( a2 + b2 )

 

 

 

 

 

 

 

 

 

 

 

 

COMPLEJOS: ECUACION DE SEGUNDO GRADO

 

Las raíces cuadradas de números negativos no tienen solución real, pero en cambio tienen solución en el conjunto de los números complejos.