1 voto | Promedio: 10

INTRO. EST. DE LAS PROGRESIONES

�

Las progresiones constituyen el ejemplo más sencillo del concepto de sucesión. Desde los albores de la historia de las matemáticas se han estudiado sus propiedades, y éstas han sido aplicadas, sobre todo, a la aritmética comercial.

El estudio de las progresiones aritméticas es paralelo al de las geométricas por cuanto las propiedades de estas últimas emanan de las primeras sin más que convertir las sumas en productos, diferencias en cocientes, y el producto por un número natural en una potencia de exponente natural.

Name=1; HotwordStyle=BookDefault; El origen de las progresiones, al igual que el de tantas otras ramas de las matemáticas, es incierto. No obstante, se conservan algunos documentos que atestiguan la presencia de progresiones varios siglos antes de nuestra era, por lo que no se debe atribuir su paternidad a ningún matemático concreto.

Es conocido el problema de calcular en cuánto tiempo se doblaría una cantidad de dinero a un determinado interés compuesto, propuesto por los babilonios (2000 a.C. - 600 a.C.), lo cual hace pensar que conocían de alguna manera la fórmula del interés compuesto y, por tanto, las progresiones geométricas.

En el libro IX de Los Elementos de Euclides aparece escrita una fórmula, semejante a la actual, de la suma de n términos consecutivos de una progresión geométrica. Bhaskara, matemático hindú del siglo XII, plantea en su más conocida obra, el Lilavati , diversos problemas sobre progresiones aritméticas y geométricas.

SUCESIONES

Se entenderá por sucesión una colección de números dispuestos uno a continuación de otro.

Sirvan de ejemplo:

b) -1, 3, 7, 11, 15...

c) 3, 6, 12, 24, 48...

En el primero no es posible averiguar qué número seguiría a 13 (no se encuentra una regla que indique la relación entre los términos). En el segundo, a 15 le seguirían 19, 23, 27... (cada término es cuatro unidades mayor que el anterior). En el tercero, al término quinto, que es 48, le seguiría 96 (cada término es el doble del anterior).

Cuando se habla de una sucesión cualquiera, la forma más usual de referirse a ella es escribir a₁, a₂, a₃, a₄, ..., a_{n - 2} , a_{n - 1} , a_n , ... donde los subíndices determinan el lugar que cada término ocupa dentro de la sucesión, y los puntos suspensivos evitan la necesidad de escribir todos los números.

Es también frecuente encontrar una sucesión simbolizada por (a_n)_nN, o simplemente (a_n).

Término general de una sucesión

El término general de una sucesión es una fórmula que permite conocer el valor de un determinado término si se conoce previamente el lugar que ocupa en la misma. Por costumbre, al término general de una sucesión se le denota por a_n y se hablará de término n-ésimo.

De entre los muchos ejemplos que se podrían citar, valgan los siguientes:

Ejercicio: determinación de términos de una sucesión

-------------------------------------------------------------------------------------------------------------------------

Resolución:

‚ Escribir los seis primeros términos de la sucesión a_n = 3 • 2^{n - 1}

Resolución:

a₁ = 3 • 2^{1 - 1} = 3 • 1 = 3 a₄ = 3 • 2³ = 24

a₂ = 3 • 2 = 6 a₅ = 3 • 2⁴ = 48

a₃ = 3 • 2² = 12 a₆ = 3 • 2⁵ = 96

-------------------------------------------------------------------------------------------------------------------------

La obtención del término general de una sucesión puede entrañar una notable dificultad. No obstante, se estudiarán a continuación dos clases de sucesiones en las que el hallazgo del término general es bastante sencillo.

PROGRESIONES ARITMÉTICAS

Una progresión aritmética es una sucesión en la que cada elemento se obtiene sumando al anterior un número fijo llamado diferencia, que se representa por la letra d .

Así, si (a_n) es una progresión aritmética, se verifica que:

a_n = a_{n - 1} + d

Ejercicio: cómo reconocer una progresión aritmética

-------------------------------------------------------------------------------------------------------------------------

Para asegurarse de que una sucesión es una progresión aritmética se ha de comprobar que la diferencia entre cada término y su anterior es siempre la misma. Además, esta comprobación elemental determina el valor de la diferencia de la progresión.

� ¿Es la sucesión 7, 5, 3, 1, -1, -3, -5 ... una progresión aritmética? Si lo es, ¿cuál es la diferencia?

Resolución:

• Se determina si la diferencia entre cada dos términos consecutivos es la misma:

5 - 7 = -2; 3 - 5 = -2; 1 - 3 = -2; -1 - 1 = -2; ...

Es una progresión aritmética de diferencia d �= -2.

Resolución:

-------------------------------------------------------------------------------------------------------------------------

Término general de una progresión aritmética

La fórmula del término general de una progresión aritmética (a_n) se encuentra sin más que observar que:

a₂ = a₁ + d

a₃ = a₂ + d = (a₁ + d) + d = a₁ + 2 d

a₄ = a₃ + d = (a₁ + 2d) + d = a₁ + 3d

a₅ = a₄ + d = (a₁ + 3d) + d = a₁ + 4d

Nótese que en todos los casos el término correspondiente es la suma de dos cantidades:

- La primera es siempre a₁

- La segunda es el producto (n - 1) d .

a_n = a₁ + (n - 1) d

• Si la diferencia de una progresión aritmética es positiva, la progresión es creciente; es decir cada término es mayor que el anterior.

• Si la diferencia de una progresión aritmética es cero, la progresión es constante, es decir, tiene todos sus términos iguales.

• Si la diferencia de una progresión aritmética es negativa, la progresión es decreciente, es decir, cada término es menor que el anterior.

Ejercicio: cálculo del término general de una progresión aritmética

-------------------------------------------------------------------------------------------------------------------------

� Sea la sucesión 1, 3, 5, 7, 9, ... ¿Cuál es su término general?

Resolución:

Se trata de una progresión aritmética de diferencia d = 2 y primer término a₁ = 1. El término general es, por tanto:

a_n = 1 + (n - 1) • 2 = 2n-1

‚ Calcular a qué altura sobre el suelo se encuentra una persona que vive en un 6.^o piso, sabiendo que los bajos del edificio tienen una altura de 4 m y que entre cada dos pisos consecutivos hay un desnivel de 2,8 m.

Resolución:

• Es claro que si se considera la sucesión de las alturas de los pisos, la diferencia entre cada vivienda y la anterior es constante e igual a 2,8 m.

Así pues, se está en el caso de una progresión aritmética en la que el primer término es 4 (altura a la que se encuentra el primer piso) y la diferencia es 2,8.

• El problema se resuelve calculando el término 6.^o:

a_n = 4 + (n - 1) • 2,8

a₆ = 4 + (6 - 1) • 2,8 = 18

-------------------------------------------------------------------------------------------------------------------------

Términos equidistantes de una progresión aritmética

El interés de las progresiones aritméticas no acaba en el cálculo del término general. Estudiando más detalladamente algunos modelos de progresiones aritméticas, se pueden deducir propiedades de enorme interés:

Name=1; HotwordStyle=BookDefault; Name=2; HotwordStyle=BookDefault; Name=3; HotwordStyle=BookDefault;

En cada uno de estos tres modelos se han elegido al azar dos parejas distintas de términos, de forma que la suma de los subíndices es igual en ambos casos. Sumando el valor de los términos en cada una de las dos parejas, se observa que los resultados coinciden.

Esto conduce a la pregunta de si, elegidas cualesquiera dos parejas de términos cuyas sumas de subíndices coincidan, también coincidirán las sumas de sus términos correspondientes.

Dicho en lenguaje matemático, cabe preguntarse si será cierto que el hecho de

ser r + s = u + v, se desprende la igualdad a_r + a_s = a_u + a_v.

La respuesta es afirmativa, y este resultado se conoce con el nombre de propiedad de los términos equidistantes de una progresión aritmética.

• Propiedad: Si a_n es una progresión aritmética de diferencia d y r + s = u + v, entonces a_r + a_s = a_u + a_v.

Demostración:

Estos dos resultados son iguales por ser r + s = u + v.

Ejercicio: cálculo de términos equidistantes en una progresión aritmética

-------------------------------------------------------------------------------------------------------------------------

� En una progresión artimética se sabe que a₁ = -2, a₃₂ = 91, a₁₆ = 43. Encontrar a₁₇.

Resolución:

Puesto que 1 + 32 = 16 + 17 = 33, por la propiedad de los términos equidistantes,

a₁ + a₃₂ = a₁₆ + a₁₇

-2 + 91 = 43 + a₁₇ � a₁₇ = 46

-------------------------------------------------------------------------------------------------------------------------

Interpolación de medios aritméticos

Interpolar (de inter , entre y polos, ejes) n números entre otros dos conocidos a y b; consiste en construir una progresión aritmética a, a₁, a₂, ... , a_n, b.

Para resolver este problema basta con conocer la diferencia que ha de tener la progresión, la cual se deduce sin más que tener en cuenta dos cosas:

1) La sucesión tiene n + 2 términos

2) El primer término es a y el término a_{n + 2} es b.

Aplicando la fórmula del término general de una progresión aritmética, se tiene que:

b = a + [(n + 2) - 1] • d ,

Una vez conocido el valor de la diferencia, a₁ se obtiene como la suma de a y d ; a₂ es la suma de a₁ y d , y así sucesivamente.

Los números a₁, a₂, ... , a_n reciben el nombre de medios aritméticos.

Ejercicio: interpolación de medios aritméticos

-------------------------------------------------------------------------------------------------------------------------

� Interpolar cinco medios aritméticos entre -18 y 25.

Resolución:

• La progresión es: -18, a₁, a₂, a₃, a₄, a₅, 25.

• Aplicando la fórmula obtenida con a = -18 y b = 25.

La progresión aritmética que se buscaba es:

-------------------------------------------------------------------------------------------------------------------------

Suma de términos consecutivos de una progresión aritmética

Se denotará por S_n a la suma a₁ + a₂ + ... + a_n

Se tiene entonces:

S_n = a₁ + a₂ + a₃ + ... + a_{n - 2} + a_{n - 1} + a_n

Invirtiendo el orden,

S_n = a_n + a_{n - 1} + a_{n - 2} + ... + a₃ + a₂ + a₁

y sumando,

2S_n = (a₁ + a₂) + (a₂ + a_{n - 1}) + ... + (a_{n - 1} + a₂) + (a_n + a₁)

Ahora bien, por la propiedad de los términos equidistantes se sabe que:

a₁ + a_n = a₂ + a_{n - 1} = a₃ + a_{n - 2} = ... = a_n + a₁

Por tanto, 2 • S_n = n(a₁ + a_n), y despejando:

Esta fórmula no sólo sirve para sumar los primeros términos de una progresión aritmética sino para sumar cualesquiera n términos consecutivos.

Para sumar, por ejemplo, a₅ + a₆ ... + a₈₃, es necesario constatar que hay

(83 - 4 = 79) 79 términos (faltan los cuatro primeros).

La suma es:

Es muy conocida la anécdota según la cual a Carl Frederich Gauss (1777-1855), cuando contaba con diez años de edad, le propusieron en la escuela primaria de su aldea natal que sumara los 100 primeros números naturales. Ante el asombro del profesor, apenas éste había acabado de dictar el problema, Gauss dio la solución: 5 050.

Lo que este insigne matemático observó fue que la suma 1 + 100 era igual a

2 + 99, igual a 3 + 98, ... etc. es decir, sólo tuvo que darse cuenta de que contaba con 50 parejas de números, cada una de las cuales sumaba 101. Así, se limitó a multiplicar: 50 • 101 = 5 050.

Name=4; HotwordStyle=BookDefault;

Ejercicio: suma de términos de una progresión aritmética

-------------------------------------------------------------------------------------------------------------------------

� Sumar los veinte primeros términos de la progresión:

-5, 4, 13, 22, 31, 40

Resolución:

• La diferencia es d = 9

• a₂₀ = -5 + (20 - 1) • 9

a₂₀ = -5 + 19•9 = 166

‚ Dada la progresión aritmética 8, 3, -2, -7, -12, ..., sumar los términos comprendidos entre a₂₄ y a₃₆.

Resolución:

• La diferencia es d = -5.

a₂₄ = 8 + 23 • (-5) = -107

a₃₆ = 8 + 35 • (-5) = -167

Entre ambos hay 36 - 23 = 13 términos.

ƒ ¿Cuántos términos de la progresión -11, -4, 3, 10, ... hay que tomar para que su suma sea 570?

Resolución:

Se sabe que:

a₁ = -11, d = 7, a_n = -11 + (n - 1) 7 = 7n - 18 y S_n = 570.

Se ha de calcular n:

1140 = 7n² - 29n

7n² - 29n - 1140 = 0

Se resuelve la ecuación de 2.� grado:

-------------------------------------------------------------------------------------------------------------------------

PROGRESIONES GEOMÉTRICAS ( I )

�

Name=1; HotwordStyle=BookDefault; Una progresión geométrica es una sucesión en la que cada elemento se obtiene multiplicando el anterior por un número fijo llamado razón, y que se representará por la letra r .

Así, si (a_n) es una progresión geométrica, se verifica

a_n = a_{n - 1} • r

Ejercicio: cómo reconocer una progresión geométrica

-------------------------------------------------------------------------------------------------------------------------

Para asegurarse de que una sucesión es una progresión geométrica se ha de comprobar que el cociente entre cada término y su anterior es siempre el mismo. Además esta comprobación elemental determina el valor de esta razón de la progresión.

� ¿Es 5, 15, 45, 135, 405 ... una progresión geométrica?

Resolución:

Resolución:

-------------------------------------------------------------------------------------------------------------------------

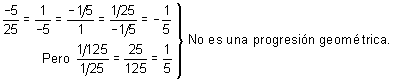
Término general de una progresión geométrica

La fórmula del término general de una progresión geométrica (a_n) se encuentra sin más que observar que:

a₂ = a₁ • r

a₃ = a₂ • r = (a₁ • r) • r = a₁ • r²

a₄ = a₃ • r = (a₁ • r²) • r = a₁ • r³

a₅ = a₄ • r = (a₁ • r³) • r = a₁ • r⁴

.......................................................

Nótese que, en todos los casos, el término correspondiente es el producto de dos cantidades:

- La primera es siempre a₁

- La segunda es una potencia de base r y exponente un cierto número, que se obtiene restando una unidad al subíndice.

En definitiva, la expresión del término general es:

a_n = a₁ • r^{n - 1}

• Si la razón de una progresión geométrica es mayor que uno, la progresión es creciente, es decir, cada término es mayor que el anterior.

• Si la razón de una progresión geométrica está comprendida entre cero y uno, la progresión es decreciente, es decir, cada término es menor que el anterior.

• Si la razón de una progresión geométrica es igual a uno, la progresión es constante, es decir, tiene todos los términos iguales.

• Si la razón de una progresión geométrica es menor que cero, la progresión es alterna, es decir, sus términos son alternativamente positivos y negativos.

Ejercicio: cálculo del término general de una progresión geométrica

-------------------------------------------------------------------------------------------------------------------------

Resolución:

• Se trata de una progresión geométrica de razón r = 3 y primer término

• El término general es, por tanto:

a_n = 3^{n - 2}

‚ ¿Cuál es el término general de la progresión -1, 2, -4, 8, -16, ...?

Resolución:

• Es una progresión geométrica en la que el primer término a₁ vale -1, y la razón es:

• Su término general es, pues:

a_n = -1 • (-2)^{n - 1}

Este tipo de progresiones geométricas recibe el nombre de progresión geométrica alternada.

-------------------------------------------------------------------------------------------------------------------------

Nótese la similitud que hasta el momento se da entre las progresiones aritméticas y las geométricas. Se seguirán comprobando todas las propiedades, sin más que cambiar sumas por productos.

Términos equidistantes de una progresión geométrica

La analogía observada hasta ahora conduce a la pregunta de si, elegidas cualesquiera dos parejas de términos cuyas sumas de subíndices coincidan, también coincidirán los productos de sus términos correspondientes.

Dicho en lenguaje matemático, cabe preguntarse si será cierto que del hecho de

ser t + s = u + v, se desprende la igualdad a_t • a_s = a_u • a_v.

La respuesta es afirmativa, y este resultado se conoce con el nombre de propiedad de los términos equidistantes de una progresión geométrica.

• Propiedad: Si en una progresión geométrica t + s = u + v, entonces a_t • a_s = a_u • a_v

Demostración:

Al ser t + s = u + v, estas dos expresiones coinciden.

Ejercicio: cálculo de términos de una progresión geométrica

-------------------------------------------------------------------------------------------------------------------------

� Encontrar el término a₁ de una progresión geométrica de la que se sabe que:

Resolución:

• Puesto que 3 + 9 = 1 + 11 = 12,

a₃ • a₉ = a₁ • a₁₁

a₁ = 81

-------------------------------------------------------------------------------------------------------------------------

Interpolación de medios geométricos

Interpolar n medios geométricos entre otros dos conocidos a y b, consiste en construir una progresión geométrica a, a₁, a₂, ..., a_n, b.

Para resolver este problema basta con conocer la razón que ha de tener la progresión, la cual se deduce sin más que tener en cuenta dos cosas:

1) La sucesión tiene n + 2 términos.

2) El primer término es a y el n + 2 es b.

Aplicando la fórmula del término general de una progresión geométrica se tiene que:

b = a • r^{n + 2 - 1}, de donde

Una vez conocido el valor de la razón, a₁ se obtiene como el producto de r por a; a₂ es el producto de a₁ por r , y así sucesivamente.

Ejercicio: interpolación de medios geométricos

-------------------------------------------------------------------------------------------------------------------------

� Interpolar cuatro medios geométricos entre 128 y 4.

Resolución:

• La progresión es 128, a₁, a₂, a₃, a₄, 4.

Aplicando la fórmula obtenida con a = 128 y b = 4:

La progresión geométrica que se buscaba es:

128, 64, 32, 16, 8, 4, ...

‚ Interpolar tres medios geométricos entre 3 y 48.

Resolución:

• Aplicando la fórmula:

Recuérdese que una raíz de índice par tiene dos soluciones, una positiva y una negativa. Así pues, en este caso, hay dos posibilidades.

• Si r = 2, la progresión es 3, 6, 12, 24, 48, ...

Si r = -2, la progresión es: 3, -6, 12, -24, 48, ...

-------------------------------------------------------------------------------------------------------------------------

Producto de términos consecutivos de una progresión geométrica

Continuando con la analogía observada, se encuentra la fórmula del producto de términos de una progresión geométrica.

Se denotará por P_n al producto a₁ • a₂ • ... • a_n.

Se tiene entonces:

P_n = a₁ •a₂ •a₃ ... a_{n - 2} •a_{n - 1} •a_n

Invirtiendo el orden P_n = a_n •a_{n - 1} •a_{n - 2} ... a₃ •a₂ •a₁

______________________________

y multiplicando P_n ² = (a₁ •a_n )(a₂ •a_{n - 1}) ... (a_{n - 1} •a₂)(a_n •a₁ )

Ahora bien, por la propiedad de los términos equidistantes se sabe que:

a₁ •a_n = a₂ •a_{n - 1} = a₃ •a_{n - 2} = ... = a_n •a₁

Por tanto P_n ² = (a₁ •a_n )ⁿ y despejando:

Para determinar el signo, ha de estudiarse cada caso concreto.

Esta fórmula no sólo sirve para multiplicar los primeros términos de una progresión geométrica, sino que también es válida para multiplicar cualesquiera n términos consecutivos, al igual que se hace en las progresiones aritméticas.

Ejercicio: cálculo del producto de términos consecutivos de una progresión geométrica

-------------------------------------------------------------------------------------------------------------------------

Resolución:

• Es una progresión geométrica de razón r = 2

Para poder escribir dicho número serían necesarias 34 cifras, lo que da idea de la gran velocidad de crecimiento que tienen las progresiones geométricas.

‚ Calcular el producto de los siete primeros términos de la progresión

1, -2, 4, -8, ...

Resolución:

• Es una progresión geométrica de razón r = -2

• a_n = 1•(-2)^{n - 1}; a₇ = 1•(-2)⁶ = 64

Para determinar el signo, obsérvese que hay tres términos negativos y al ser este número impar, el producto de todos ellos es negativo.

Así pues, P₇ = -2²¹

-------------------------------------------------------------------------------------------------------------------------

Suma de varios términos consecutivos de una progresión geométrica

Name=2; HotwordStyle=BookDefault; Se denotará por S_n a la suma de n términos consecutivos de una progresión geométrica:

S_n = a₁ + a₂ + ... + a_{n - 1} + a_n

Para obtener una fórmula que permita hacer este cálculo de un modo rápido, se multiplican ambos miembros de la igualdad por la razón:

S_n • r = (a₁ + a₂ + ... + a_{n - 1} + a_n ) • r

S_n • r = a₁ •r + a₂ •r + ... + a_{n - 1} •r + a_n •r,

y teniendo en cuenta que al multiplicar un término por la razón se obtiene el término siguiente,

S_n • r = a₂ + a₃ + ... + a_n + a_n • r

Restando ahora a esta igualdad la primera:

S_n • r = a₂ + a₃ + ... + a_n + a_n • r

S_n = a₁ + a₂ + ... + a_{n - 1} + a_n

����������������

S_n • r - S_n = -a₁ + a_n • r

S_n (r - 1) = a_n • r - a₁

Despejando S_n,

Name=3; HotwordStyle=BookDefault; Esta fórmula que da la suma de n términos consecutivos de una progresión geométrica tiene otra versión igualmente útil si se expresa el término general a_n como a₁ • r^{n - 1}:

Ejercicio: suma de términos de una progresión geométrica

-------------------------------------------------------------------------------------------------------------------------

� Sumar los quince primeros de la progresión geométrica 3/2, 9/2, 27/2 ...

Resolución:

‚ Sabiendo que 3 es el primer término de una progresión geométrica y 1 875 el quinto, calcular la suma de esos cinco términos.

Resolución:

• a₅ = 1875 = 3•5⁴ = a₁•r⁴ � r⁴ = 5⁴ � r = �5

ƒ Sumar los términos comprendidos entre el tercero y el vigésimo lugar de la

Resolución:

-------------------------------------------------------------------------------------------------------------------------

Suma de todos los términos de una progresión geométrica ilimitada decreciente

Una progresión geométrica es decreciente (cada término es menor que el anterior),

La relevancia de este apartado es que se trata de sumar todos los términos de la progresión y no una parte de ellos. Obsérvese que en el caso de una progresión creciente (cada término mayor que el anterior), la suma de todos los términos de la misma será infinito, independientemente del valor de los términos. No ocurre así para el caso de progresiones decrecientes.

Partiendo de la fórmula

donde r es un número comprendido entre cero y uno y n el número de términos de la progresión (infinito), la potencia rⁿ es una cantidad tan pequeña (tiende a cero), que se puede despreciar. Recuérdese que el resultado de una potencia cuya base está comprendida entre cero y uno va disminuyendo a medida que aumenta el exponente.

Se tiene entonces:

o bien

PROGRESIONES GEOMÉTRICAS ( II )

�

Cómo se suman los términos de una progresión geométrica de razón

-1 < r < 1

Si r es un número mayor que -1 y menor que 1, rⁿ se aproxima tanto más a cero cuanto más grande sea n; matemáticamente esto se expresa diciendo que rⁿ tiende a cero.

Obsérvese cómo, por ejemplo, (1/2)² = 1/4 = 0,25

(1/2)³ = 1/8 = 0,125

(1/2)⁴ = 1/16 = 0,0625

...............................................

(1/2)²⁰ = 1/1048576 = 0,0000009

Y de igual modo (-1/2)² = 1/4 = 0,25

(-1/2)³ = 1/8 = -0,125

(-1/2)⁴ = 1/16 = 0,0625

................................................

(-1/2)²⁰ = 1/1048576 = 0,0000009

Ejercicio: suma de infinitos términos de una progresión geométrica ( |r |< 1)

-------------------------------------------------------------------------------------------------------------------------

� Calcular la suma de todos los términos de la progresión: 0,3; 0,15; 0,075;...

Resolución:

• Se trata de una progresión geométrica decreciente cuyo primer término

‚ Sumar todos los términos de la progresión geométrica -7, 7/3, -7/9, 7/27...

Resolución:

ƒ En un triángulo equilátero de 6 metros de lado, se unen los puntos medios de sus lados, obteniéndose así otro triángulo inscrito en el primero. Este proceso se repite indefinidamente. Calcular la suma de las áreas de todos los triángulos formados.

Resolución:

Name=1; HotwordStyle=BookDefault;

• Se trata aquí de sumar todos los términos de una progresión geométrica ilimitada cuya razón es menor que uno, puesto que las áreas de los triángulos que se van formando son cada vez menores.

• El primer término de la progresión será el área del primer triángulo:

primero.

„ Dado un círculo de radio r, se construye un segundo círculo cuyo diámetro sea el radio del anterior, un tercero cuyo diámetro sea el radio del segundo y así sucesivamente. ¿Cuál será la suma de las áreas de todos los círculos así formados?

Resolución:

Name=2; HotwordStyle=BookDefault;

• Como en el caso anterior, se trata de sumar todos los términos de la progresión geométrica que forman las áreas de los círculos.

• Se observa que se trata de una progresión geométrica decreciente de

-------------------------------------------------------------------------------------------------------------------------

Entre las progresiones aritméticas y las geométricas se pueden apreciar notables diferencias. Estas últimas crecen mucho más deprisa (si la razón es mayor que la unidad) que las progresiones aritméticas; o decrecen de manera tan vertiginosa que incluso es posible sumar una cantidad infinita de números y obtener un resultado tan inesperado como sorprendentemente pequeño, cuando la razón, en valor absoluto, es menor que la unidad, como ya se ha visto.

Sirva como ilustración de cuanto se acaba de decir, la siguiente situación:

Piénsese en dos personas (de economías solventes) que acuerdan que uno dará al otro dos millones de pesetas el primer día de mes; cuatro millones al día siguiente; seis el tercero, y así, sumando dos millones diarios hasta completar el mes. Simultáneamente, el segundo dará al primero una peseta el primer día; dos pesetas, el segundo; cuatro, el tercero, y así sucesivamente, duplicando la cantidad del día anterior, hasta cumplir el plazo asignado de treinta días. ¿Quién obtendrá mayores beneficios?

El primero, la última jornada desembolsa

a₃₀ = 2 + (30 - 1) 2 = 60; 60 millones

Por su parte, el otro amigo aporta (1 + 2 + 4 + ... + 2²⁹) pesetas. Sin más que hacer uso de la fórmula de la suma de los términos de una progresión geométrica, se tiene que la cantidad es:

De otro lado, los números a que dan lugar las progresiones geométricas serían sencillamente increíbles (de hecho, son increíbles para muchas personas) a poco que se dudase de la exactitud de las matemáticas.

Piénsese en un folio de 1/20 mm de espesor; es decir, veinte folios bien prensados tendrían un grosor de 1 mm. Si se dobla el papel por su mitad; se vuelve a doblar otra vez por la mitad, y se continúa este proceso hasta repetirlo 50 veces, ¿qué grosor tendría el trozo de papel resultante?

Es claro que en la quincuagésima operación de plegado, se tendría un grosor de

2⁵⁰ veces el espesor inicial, es decir,

2⁵⁰/20 mm; o también,

2⁵⁰/200 cm; o bien,

2⁵⁰/20000 m; o mejor aún,

2⁵⁰/2000000 km.

Haciendo las oportunas operaciones; resulta que el grosor del tan citado papel es de

��56 295 500 km!!

Compárese este dato con la distancia media de la Tierra a la Luna, que es de

385 000 km.