Definición:
Llamamos serie
de potencias a toda expresión
del tipo
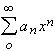, en donde 
Es
decir
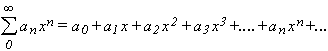
Por
ejemplo
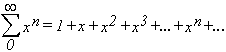
en
donde todos los 
valen 1, o
y
todos sus 
.
Es
interesante saber cuáles son los valores de x Î R para los que las respectivas series funcionales se
convierten en series numéricas convergentes. Por ejemplo si en la primera de
las dos series anteriores hacemos x=0, 
es 1 + 0 + 0 +....+ 0
+... y esta serie es
obviamente convergente. En cambio si x = 1, se convierte en 1 + 1 +... +... que
es divergente.
Pero
para x = 1/2 es
que
es una serie geométrica de razón 
y su suma 
con lo que la serie es convergente. Más aún,
es una serie
geometrica de razón x y será
convergente si 
, es decir si 
,
siendo 
.
Si
se cumple esta condición:
Entonces
bajo ciertas condiciones, una serie de potencias describe exactamentea a una
función. En este caso a 
, pero sólo en el intervalo (-1;1).
Gráficamente
|
1
|
sólo definida en la
parte marcada gruesa por la serie
Si en el segundo ejemplo tomamos x =1, se convierte en
Intervalo de convergencia: Se llama intervalo de convergencia I al conjunto de
valores reales de x que convierte a la serie de potencias
en una serie numérica convergente.
Radio de convergencia: Lamamos así a la menor de las cotas superiores del
conjunto I.
En el caso de 
se observa que el
intervalo de convergencia es I = (-1;1) y el radio de convergencia es R = 1.
Se observa que el intervalo I está centrado en el origen. Siempre es
asi para el I de 
.
Cálculo del radio e intervalo de convergiencia:
Sea la serie de potencias 
. Formemos la serie de valores absolutos, es decir
que es
una serie de términos positivos que si converge arrastrará la convergencia de 
que no necesariamente
es de términos positivos.
La convergencia de 
la estudiaremos con
el criterio de D'Alembert, o sea si
será convergente.
Desarrollando
y entonces la serie converge para
ó 
Llamamos R al
y además 
.
Para 
todos los valores de
an=1, 
, en cambio para 
es 
y el I = R
Series de McLaurin y Taylor:
Sea la fórmula de McLaurin
siendo 
con 0 < z < x.
Es decir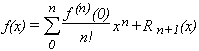 
.
Llamaremos serie de MacLaurin asociada a una función f(x) a la
expresión
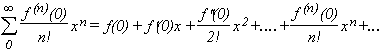
Esta serie describe exactamente a la función f(x) cuando coincida con la fórmula de McLaurin y para ello
deberá cumplirse que:
1)Se trabaje en el intervalo de convergencia de la serie y
2)
.
Ejemplo: Sea f(x) = ex
Veremos si
.
que 
.
Ejercicio:
Desarrollar f(x) = sen x en serie de potencias.
f(x) = senx ; f(0)=0
f'(x) = cosx ; f '(0)=1
f"(x)= -senx; f"(0)=0
f"'(x)= -cosx ; f"'(0)=-1
fIV(x)= senx ; fIV(0)=0
fV(x)= cosx ; fV(0) =1 y generalizando
pero en todo caso siempre son en valor absoluto
menores que 1, y finalmente
con lo que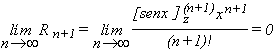 
y finalmente
Estudiemos el intervalo de convergencia
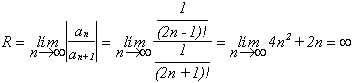y por lo tanto I = R
Monografías
(7 / 10) |
Sin comentarios | 
