Conceptos generales de campos

Envia tus archivos, resúmenes, monografías, etc.

Introducción. Definición. Formalismo matemático. Flujo de un campo vectorial. Gradiente de un campo. Ley de Gauss. Circulación. Representación gráfica de los campos. Campo escalar. Campo vectorial.

Agregado: 22 de JULIO de 2003 (Por Michel Mosse) | Palabras: 1295 | Votar | Sin Votos | Sin comentarios | Agregar Comentario
Categoría: Apuntes y Monografías > Física >
Material educativo de Alipso relacionado con Conceptos generales campos

Biografia y vida de Pedro Albizú Campos: Breve Biografia de Pedro Albizú Campos

Campos de Castilla.: Campos de Castilla, El retrato de Machado, El Paisaje castellano, Campos de Soria, El campo andaluz, España, Desde mi rincón, Las gentes, La visión del pasado, del futuro y del presente de España por Antonio Machado.

Conceptos de psicología científica, sociogénesis, positivismo y socioconstructivismo: ...

Enlaces externos relacionados con Conceptos generales campos

Conceptos generales de campos

Introducción

En bastantes campos de la física se trata el concepto de campo, introduciéndole de forma más o menos intuitiva y formulandolo después rápidamente para después realizar con él algunos cálculos. De todas formas parece más conveniente analizar ahora algunos conceptos de manera un poco más rigurosa para poder luego entender mejor la visión que sobre la física aportan los campos.

Definición

Se denomina campo a todo objeto matemático que esté definido para cualquier punto del espacio. En física una magnitud es un campo cuando está definida en todo el espacio. Si esta magnitud es un número, un escalar, tendremos un campo escalar, si es en cambio un vector, será un campo vectorial.

Por ejemplo, en un día con mucho viento, la temperatura que haga en cualquier parte de una ciudad será un campo escalar. Así podemos decir que en el punto ``tal'' existen tantos grados de temperatura y en el ``cual'' otros ciertos grados de temperatura. Dado cualquier punto de la ciudad diciendo que temperatura hace tendremos un campo escalar (de temperaturas). Si para esta misma ciudad tomamos la intensidad y dirección del viento como un vector tendremos un campo vectorial. Análogamente podremos decir: En este punto el vector de la velocidad del viento es tanto, pero en este otro punto es cuanto. Tendremos definida una cierta magnitud vectorial en todos los puntos del espacio.

Formalismo matemático

Para describir matemáticamente un campo bastará con indicar cuánto vale la magnitud que nos interese en todos los puntos del espacio indicada por una cierta función. Para un campo escalar tendremos que o quizás también del tiempo . Por ejemplo, si queremos definir el campo escalar distancias al origen de coordenadas tendremos que $M=\sqrt{x^2+y^2+z^2}$ y así hemos cumplido la definición de campo escalar. Dado un punto del espacio tenemos bien escrita una magnitud para ese punto. En el punto la magnitud, en este caso, es $\sqrt{3}$ .

Un campo vectorial se define de manera análoga, pero teniendo en cuenta que deberemos aportar las tres componentes del vector. Podemos denotarlo como $\vec{M} = \vec{f}(x,y,z)$ o también como

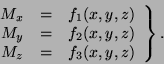
$\begin{displaymath}\left.\begin{array}{ccc} M_x & = & f_1(x,y,z) \\ M_y & = & f_2(x,y,z) \\ M_z & = & f_3(x,y,z) \end{array}\right\}.\end{displaymath}$

Un ejemplo (que representa una fuerza cualesquiera) de campo vectorial sería

$\begin{displaymath}\vec{M}(x,y,z) = x^2 \hat{\imath}+ y^2 \hat{\jmath}+ xy \hat{k}.\end{displaymath}$

Flujo de un campo vectorial

Se define el flujo de un campo vectorial como la cantidad de campo que atraviesa cierta área. Como esta definición hablada es un poco pobre, matemáticamente si tenemos un campo vectorial $\vec{M}$ que atraviesa una pequeña región tomamos como $d\phi = MdS$ . Ahora bien, no es lo mismo que la superficie que atraviese sea perpendicular al campo, en cuyo caso entraría ``de lleno'' a que dicha superficie esté situada de forma paralela, pues en este último caso no atravesaría nada de campo. Por esto se define un vector $d\vec{S}$ que sea perpendicular a la pequeña área considerada y tener así que $d\phi = \vec{M}\cdot d\vec{S}$ . Con esto logramos que aparezca el término $\cos \theta$ en la definición de flujo y poder así considerar la proyección correcta de campo que atraviesa la superficie. Para lograr tener el flujo total no hay más que integrar:

$\begin{displaymath}\phi_M = \int_S \vec{M}\cdot\vec{S}.\end{displaymath}$

Gradiente de un campo

$\circ$ Dada una fuerza conservativa ya hemos visto anteriormente como se podía extraer de un potencial, lo cual reportaba la ventaja de que una fuerza conservativa no es sino un campo vectorial, y por tanto tendrá tres dimensiones, frente a un potencial, que puede ser considerado un campo escalar y por tanto presenta sólo una dimensión.

La operación por la cual lográbamos esto la llamamos gradiente, y teníamos que $\vec{F}=-\vec{\nabla}V$ .

Así pues la operación gradiente es una forma de, a partir de un campo escalar, lograr otro vectorial y, como hemos visto en el párrafo anterior, este campo nuevo será un campo de fuerzas si el otro era un potencial.

Ley de Gauss

Si tomamos una fuerza central que decrezca con el cuadrado de la distancia, es decir, del tipo $\vec{F}=C \frac{\widehat{r}}{r^2}$ donde es una constante cualquiera, y calculamos su flujo a través de una superficie esférica centrada también respecto al origen, como la fuerza, de radio tendremos que

$\begin{displaymath}\phi = \int_S C\frac{\widehat{r}}{r^2} \cdot d\vec{S}\end{displaymath}$

y aquí considerando que para este caso la fuerza siempre corta perpendicularmente a nuestra esfera, y la distancia a ella siempre es tendremos, extrayendo las constantes y realizando el producto escalar

$\begin{displaymath}\phi = \frac{C}{R^2} \int_S dS\end{displaymath}$

que, simplemente, dará $\phi = \frac{C}{R^2} 4\pi R^2$ y, por tanto

$\begin{displaymath}\phi = 4\pi C.\end{displaymath}$

Esta ley encontrada para un caso muy particular, se puede demostrar no obstante, que sirve también tomando un campo gravitatorio o electrostático cualquiera y una superficie cerrada cualquiera. Por tanto, cualquiera que sea la superficie que tomemos

$\begin{displaymath} \phi = 4\pi K q, \end{displaymath}$

(10.1)

donde es la carga encerrada por la superficie, para el caso electrostático, o bien

$\begin{displaymath} \phi =-4\pi G m, \end{displaymath}$

(10.2)

siendo ahora la masa total que encierra la superficie.

Este resultado, en cuya demostración general no vamos a entrar, resulta muy importante y útil, ya que es práctico para resolver bastantes problemas, y se conoce con el nombre de Ley de Gauss para el campo electrostático o gravitatorio, en honor de su descubridor.

Circulación

$\circ$ Se define la circulación de un campo vectorial $\vec{M}$ a lo largo de un recorrido como la integral a lo largo de la línea de la componente del campo que es paralela a dicha línea.

Esta definición se puede expresar matemáticamente como

$\begin{displaymath}\int_L \vec{M}\cdot\vec{l}.\end{displaymath}$

Como podemos observar esta nueva magnitud, la circulación. no es más que la definición matemática de una magnitud física que ya conocemos: el trabajo.

Representación gráfica de los campos

Campo escalar

Representar un campo escalar se puede realizar por medio de sus superficies de nivel, es decir, uniendo con una línea todos los puntos que presente el mismo potencial, y observando estos dibujos tendremos una idea de cómo se comporta este campo. Un ejemplo podrían ser las líneas de nivel de un mapa geográfico. En él se indican cuanto vale en cada punto la altura. Basta echar una ojeada a un mapa geográfico para, observando dónde se acumulan más líneas de nivel saber que en esos puntos la pendiente será mayor.

$\circ$ Además, en este ejemplo, el campo escalar de las alturas coincide (salvo una constante) con el campo escalar potencial gravitatorio. De esta manera un punto donde hay muchas líneas de nivel supone un punto donde hay mucha variación de energía potencial. La variación la proporciona la derivada del escalar, en este caso el gradiente. Si esta derivada es alta el gradiente será considerable. Pero el gradiente de un potencial con signo menos es la fuerza que se siente en ese punto. ¿Cómo entender esto desde nuestro mapa geográfico?, es sencillo, allí donde las curvas de nivel están muy juntas el terreno es muy empinado, tiene mucha pendiente, y la fuerza que se ejerce sobre nosotros en esos puntos será muy pronunciada (hacia arriba o hacia abajo) porque el gradiente lo es. O escrito de otra forma ¿quién no ha sentido la dificultad de subir o bajar por un terreno muy escarpado?. Esta dificultad que nos proporcionan las fuerzas gravitatorias se puede ya ver gracias a la representación de un mapa con líneas de nivel.

Campo vectorial

Aunque representar un campo vectorial no es sencillo una manera de hacerlo es mediante el concepto de las líneas de fuerza, que son líneas tangentes en todo punto a la dirección del campo. Si el campo fuera uno de velocidades estas líneas coincidirían con las trayectorias de las partículas sometidas a dicho campo. Algunas propiedades de estas líneas es que no pueden cortarse^10.1 pues, si así fuera, tendríamos que en ese punto habría dos valores para el mismo campo. Para lograr que estas líneas nos hablen del módulo del campo (es decir, de su intensidad) se dibujan de tal manera que la densidad de líneas sea proporcional a dicho módulo.

Cuando un campo es conservativo, a los puntos donde las líneas convergen, se juntan, se denominan sumideros, y a aquellos de donde surgen o nacen fuentes. Así cualquier planeta es un ``sumidero'' de campo gravitatorio, y un protón sería una ``fuente'' de campo electrostático.