|
|
La dilatación del tiempo y la contracción de longitud de Lorentz-Einstein
|
Se demuestra primero que las Transformaciones de Lorentz de la relatividad especial de Einstein son contradictorias. En segundo lugar se presenta una alternativa a las Transformaciones de Lorentz, las transformaciones relacionales, que preservan la constancia local de la velocidad de la luz. Finalmente, mediante estas nuevas transformaciones, se analizan conceptos como la dilatación del tiempo y la contracción de Lorentz de la relatividad especial.
Agregado: 22 de ENERO de 2010 (Por Xavier Terri Castañé) | Palabras: 3252 | Votar |
1 voto 
| Promedio: 2
|
1 comentario - Leerlo | Agregar Comentario | Promedio: 2
Categoría: Apuntes y MonografÃas > FÃsica >
Material educativo de Alipso relacionado con dilatación del tiempo contracción longitud Lorentz-Einstein
Enlaces externos relacionados con dilatación del tiempo contracción longitud Lorentz-Einstein
Autor: Xavier Terri Castañé (xaterri@gmail.com)
 Este apunte fue enviado por su autor en formato DOC (Word).
Para poder visualizarlo correctamente (con imágenes, tablas, etc) haga click aquí o aquí si desea abrirla en ventana nueva. |
<
SOBRE LA DILATACIóN DEL TIEMPO Y LA CONTRACCIóN DE LONGITUD DE LORENTZ-EINSTEIN
Xavier Terri Castañé
ABSTRACT: Se demuestra primero que las Transformaciones de Lorentz de la relatividad especial de Einstein son contradictorias. En segundo lugar se presenta una alternativa a las Transformaciones de Lorentz, las transformaciones relacionales, que preservan la constancia local de la velocidad de la luz. Finalmente, mediante estas nuevas transformaciones, se analizan conceptos como la dilatación del tiempo y la contracción de Lorentz de la relatividad especial.
Keywords: Transformaciones de Lorentz, transformaciones relacionales, tiempo de retardo, intervalo temporal, variación de posición, intervalo espacial o longitud, Lorentz, Einstein, Galileo, Newton, Leibniz, teoría relacional, teoría conectada, relatividad del movimiento.
LAS TRANSFORMACIONES DE LORENTZ
La teoría de la relatividad especial de Albert Einstein se sustenta en las transformaciones de Lorentz.
Las transformaciones de Lorentz directas
de 
se escriben:
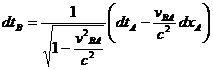
Las transformaciones de Lorentz inversas se obtienen intercambiando las etiquetas A y B. (Tanto las unas como las otras pueden ser consultadas en cualquier libro de texto sobre relatividad especial.)
Según las antiguas transformaciones de
Galileo-Newton, el tiempo no era relativo. Pero según las
transformaciones de Lorentz, el tiempo sí es relativo, relativo a la
velocidad 
. Por ejemplo, el tiempo que la secundera de un reloj C
tarda en ir de una división hasta la siguiente división (propiamente 1 segundo
según C) no es el mismo, según la relatividad especial, para A que para B. La
relación entre los tiempos de A y B para el reloj C viene dada por la primera
de las 4 anteriores transformaciones de Lorentz.
De la primera transformación de Lorentz
se deduce, haciendo 
, la famosa ‘dilación del tiempo de Lorentz-Einstein':
Haciendo 
en las
transformaciones de Lorentz inversas se obtiene ahora la famosísima dilatación
del tiempo de Einstein-Lorentz, o la de Lorentz-Einstein, que es la misma:
A
no ser que 
, es obvio que estas dos fórmulas no pueden ser ciertas
a la vez. Algebraicamente se repugnan entre sí ¿A cuál de los dos relojes, A o B, es al que le corresponde el tiempo
propio? Ya que no pueden ser ciertas a la vez, ¿a cuál de las dos anteriores
fórmulas hay que rechazar? Respuesta: las 2. Puesto que ‘velocidad' es un
concepto relativo, la teoría de la relatividad, que aún diferencia entre
referenciales inerciales y referenciales no-inerciales y entre velocidades verdaderas
y velocidades aparentes, no aporta ningún criterio sensato que permita
discernir ninguna verdad sensata. Ya he hablado sobre ello en otros lugares
(véase el artículo La contradicción de los gemelos, en el blog Einstein
vs Teoría Conectada).
Lo que ahora quería resaltar es algo distinto. Según las transformaciones de Lorentz, el tiempo entre dos sucesos (entre un tic y un tac del reloj C, por ejemplo) es relativo a la velocidad relativa de B con respecto a A, que es la misma (salvo signo) que la de A con respecto a B. De donde se deduce que las transformaciones de Lorentz son tan absurdas como afirmar 2=3. Y lo demuestro. Si se admite que el tiempo es relativo a la velocidad entre los relojes A y B, entonces, por la misma razón, también se deberá admitir que el tiempo es relativo a todas las velocidades posibles. En el caso concreto que ahora nos ocupa, aparte de la velocidad entre A y B, la velocidad entre A y C y la velocidad entre B y C.
Ante el problema de la relatividad del tiempo, la teoría de la relatividad de Einstein tan sólo tiene a priori 2 opciones lógicas: 1) si el tiempo no es relativo a la velocidad, entonces las transformaciones de Lorentz son falsas, y 2) si el tiempo sí es relativo a la velocidad, entonces es relativo a todas las velocidades posibles, y las transformaciones de Lorentz, que tan sólo hacen intervenir a una de las 3 velocidades posibles, son falsas.
Tenemos 3 relojes, no sólo 2, luego sus 3 velocidades relativas deberán aparecer en las fórmulas de unas ecuaciones de transformación que pretendan ser consideradas verdaderas (estás 3 velocidades se relacionan ulteriormente a través de la "suma" relacional de velocidades, que coincide con la conocida suma de velocidades de la relatividad especial).
Las transformaciones de Lorentz afirman que el tiempo sí es relativo a la velocidad. Pero de las 3 velocidades relativas posibles entre A, B y C tan sólo utilizan la velocidad entre A y B e ignoran las otras 2. Luego "contradicen en 2/3" su propia afirmación, luego son contradictorias (no existen contradicciones fraccionarias: algo no es contradictorio o sí lo es), luego las transformaciones de Lorentz-Einstein son falsas.
El lenguaje matemático per se no garantiza la verdad de lo que expresa. Matemática mal interpretada nunca será física. Además de ser contradictorias, las transformaciones de Lorentz de Einstein son incompatibles con la absoluta relatividad del movimiento. No saben reconocer que incluso en ausencia de gravedad y de aceleraciones relativas, la constante "c" debe limitarse a representar la velocidad local de la luz (ver el artículo La nueva revolución copernicana). Son un mero entretenimiento matemático sin sentido físico.
LAS TRANSFORMACIONES RELACIONALES
Tan sólo nos limitaremos a presentar aquí las nuevas transformaciones relacionales. El lector interesado en comprobar su deducción puede consultar La paradoja de los gemelos de la teoría de la relatividad especial de Einstein en Bubok.com o en Google.
Transformaciones relacionales directas para 
:
Las transformaciones relacionales preservan la constancia local de la velocidad de la luz para todos los observadores con independencia de sus velocidades relativas.
TIEMPO DE RETARDO E INTERVALO TEMPORAL
Einstein pone el conocido ejemplo de un
observador A que, estando en reposo junto a la vía del tren, observa dos rayos
que caen en sendos extremos de la vía C y D. El observador A se encuentra en el
punto medio de los dos sucesos C y D. En el ejemplo concreto que plantea
Einstein, los dos rayos son simultáneos para A. Y entonces pregunta: ¿son
también simultáneos para un segundo observador B que pase junto a A, en el
sentido de C hacia D, viajando en el tren a la velocidad relativa constante ?
El observador B se acerca a D y se aleja de C. A no ser que la velocidad de propagación de la luz fuese infinita, el rayo en D cae antes, según B, que el rayo en C. No hay la menor duda: si los dos rayos en C y D son simultáneos para A, entonces es imposible que lo sean para B. A y B asignan distintos tiempos a la caída de los rayos en C y D. Pero, ¿significa esto también que los tiempos de A y B transcurren a un distinto ritmo?
Einstein resalta, no le falta razón, que las coordenadas temporales para A no son las mismas que las coordenadas temporales para B. Mediante su sencillo ejemplo consigue destacar que, en diferentes sistemas de referencia, las coordenadas temporales resultan ser distintas. Y, según pretende Einstein, la presente historia también demuestra que el tiempo es relativo.
¿Qué significa ‘relativo'? Hay infinitas acepciones de ‘relativo'. La presente declaración de Einstein sobre la relatividad del tiempo está sustentada en las transformaciones de Lorentz. Es una declaración precipitada por su ansia de intentar explicar la sorprendente e inesperada constancia local de la velocidad de la luz sin invocar la "materia oscura" de su época, el inexistente y oscuro éter lumínico. Dicha declaración da lugar, como es bien sabido, a paradojas y contradicciones lógicas. Los genios suelen precipitarse... El tiempo será relativo dependiendo de lo que queramos entender por relativo.
De la no simultaneidad general de todos los sucesos nunca es lícito inferir que el ritmo en el devenir del tiempo sea relativo para distintos entes. Y ni mucho menos relativo en la manera en que las transformaciones de Lorentz, el sustento teorético de la relatividad especial de Einstein, entienden la relatividad del tiempo. Es del todo cierto que dos sucesos que puedan ser simultáneos para un observador determinado dejan de serlo, en general, para cualquier otro posible observador. En este sentido, hasta Newton, el mismísimo inventor del tiempo absoluto, estaría de acuerdo en que las coordenadas temporales son relativas. Pero Newton nunca atribuiría este tipo tan especial de "relatividad" del tiempo a que distintos entes puedan envejecer a un ritmo temporal distinto y descompasado. Desimetrizado. Lo atribuiría, con pleno sentido, a la velocidad finita, no infinita, de propagación de la luz.
Definiremos dos conceptos:
1) Variación en el tiempo de retardo:
Diferencia en las coordenadas temporales asignadas a un solo ente C. El tiempo
de retardo no es el mismo según A que según B: 
. Luego la variación: 
2) Intervalo temporal: Diferencia
temporal entre dos entes sucesivos C y D. Los dos entes son los extremos
temporales de una entidad cuyo intervalo temporal según A es: 
. Y según B: 
La semiótica éntica de la teoría relacional facilita el manejo de todo este tipo de conceptos.
En el ejemplo de las vías del tren de
Einstein el observador A está en reposo con respecto a los puntos C y D y
situado en el punto medio del segmento CD. Por tanto: 
y 
. Supondremos
también que A está situado en su origen de coordenadas y que 
.
De la primera de las 4 transformaciones relacionales es fácil deducir, suponiendo las condiciones iniciales habituales y haciendo "C=D":
Puesto que 
:
El segundo término del paréntesis es debido a la velocidad finita de la luz. La variación en el tiempo de retardo para D según A y B:
Como B se dirige hacia D, su velocidad
con respecto a A es positiva: 
. Como también lo es 
, resulta que la diferencia en el tiempo de retardo
para D según B y A es negativa y, por tanto: 
. Es decir, B ve el rayo D antes que A. Cosa lógica si
tenemos en cuenta que es B, y no A, el que se dirige hacia D.
Las coordenadas temporales para D según A y B son, como bien dice Einstein, distintas. Cosa que equivale a decir que la diferencia entre las respectivas coordenadas temporales para D según A y B no es nula. Pero esto nunca significa, necesariamente, que el tiempo transcurra a un ritmo distinto para B que A, pues la única causante de que el término del segundo miembro de la anterior ecuación no sea nulo es la velocidad finita de propagación de la luz. No existe otra causa o razón suficiente.
(Sólo para el que quiera ejercitarse en el empleo de las coordenadas relacionales aplicadas al ejemplo precedente de Einstein de los rayos sobre las vías del tren.)
Por la transformación relacional temporal:
y dado que es negativa, la
variación en el tiempo de retardo para C según A y B:
resulta ser positiva: 
Es decir, B ve
el rayo C después de A. Cosa lógica, pues es B, y no A, el que se está alejando
de C.
De las dos últimas ecuaciones se obtiene la ‘diferencia de simultaneidad para C y D según A y B':
donde 
es la distancia
entre C y D.
Puesto que C y D son simultáneos
para A, 
, se obtiene que para B son no simultáneos, y que están
temporalmente distanciados según:
Pero no hay que confundir
el tiempo de retardo con el intervalo temporal. Cosa que queda trivialmente
demostrada por el hecho de que si 
, entonces C y D serían también simultáneos, no
sucesivos, para B.)
Las anteriores fórmulas tan sólo hacen referencia a tiempos de retardo debidos a la velocidad finita de propagación de la luz. La diferencia entre los tiempos de retardo para C o D según B y A no significa que A y B envejezcan a ritmos distintos.
INTERVALO TIEMPORAL
Sean C y D dos entes sucesivos. Primero C, luego D. Supongamos que tienen sus respectivas ocurrencias, según A, en el mismo punto de su referencial A (el tic, luego el tac del reloj del lector acontecen, según el propio lector A, en un mismo punto). Entonces, según B, sus respectivas ocurrencias tienen lugar en diferentes puntos de su referencial B. Por definición de tiempo propio, es el ente A, y no B, el que mide el intervalo de tiempo propio entre C y luego D.
Puesto que ocurren en el mismo punto según A:
Además para que puedan tener su ocurrencia en el mismo punto según A, los entes C y D tienen que haber permanecido en reposo con respecto a A:
La primera transformación relacional nos permite escribir:
Todavía la primera:
Teniendo en cuenta las 4 fórmulas precedentes, el intervalo temporal entre C y D según B es,
, el mismo que según A.
Tanto A como B miden el mismo intervalo temporal entre C y luego D.
La dilatación de tiempo de Lorentz-Einstein no existe (cosa que ya habíamos demostrado, mediante el argumento del reloj lumínico y sin fórmulas matemáticas, en el artículo ‘La relatividad del tiempo. El tiempo de la relatividad'.)
VARIACIóN DE POSICIóN E INTERVALO ESPACIAL
A nadie conviene que las inteligencias se confundan. Del mismo modo que no conviene confundir la variación en los tiempos de retardo para un solo ente C según B y A con una hipotética relativización del intervado temporal entre dos entes sucesivos C y luego D según A y B, tampoco conviene confundir la variación en la posición con una hipotética relativización del intervalo espacial o de la longitud.
El libro que el lector está leyendo en este preciso momento, es un ente que siempre permanece posicionado, desde la perspectiva del propio lector, en el mismo lugar del espacio. En cambio, visto desde la perspectiva de un imaginario observador que habitara en el sol, este mismo libro, puesto que la tierra se mueve con respecto al sol a una velocidad relativa de unos 30 km/s, se ha convertido en un ente cuya posición está variando sin cesar a través del espacio. Cada nuevo segundo varía sin pausa su posición precedente. Sus nuevos lugares en el espacio relacional avanzan 30 incesantes kilómetros con respecto a los lugares precedentes cada segundo anterior. El inmóvil libro del lector, desde el punto de vista del observador solar, es un ente móvil que nunca permanece estático en el mismo lugar.
En este sentido, hasta Newton, el mismísimo inventor del espacio absoluto, estaría de acuerdo en que ‘variación de posición' es un concepto relativo.
Ambos observadores, el lector y el observador solar, ven muy distintas variaciones de posición para el mismo libro. Pero ¿difieren también éstos en cuanto a su longitud? Tal vez coincidan, por qué no, en que la longitud del libro pueda ser la misma para ambos. Sin contracción de Lorentz-Einstein.
Definamos dos conceptos:
1) Variación en la posición:
Diferencia de las coordenadas espaciales asignadas a un solo ente C en dos
instantes distintos de tiempo. No es la misma según A que según B: 
2) Intervalo espacial o longitud:
Distancia espacial entre dos entes C y D en reposo relativo en el mismo
instante de tiempo. Los dos entes son los extremos espaciales de una entidad
cuya longitud según A es 
Y según B: 
Tanto la variación de posición como la longitud vienen dadas por las transformaciones relacionales. Nos ocuparemos aquí de la longitud.
INTERVALO ESPACIAL O LONGITUD
La longitud de una vara de medir en
reposo con respecto a B es la distancia entre sus extremos D y C en el mismo
instante de tiempo relacional 
. La longitud entre D y C según B es:
y según A:
De la segunda de las 4 transformaciones relacionales es fácil deducir:
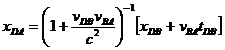
y:
Como la vara de medir está en reposo con
respecto a B (cosa que significa que se mueve con respecto a A a la velocidad: 
): 
.
Por tanto, la longitud entre D y C según A,
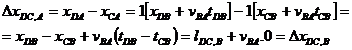
, es la misma que según B.
Tanto A como B miden la misma longitud.
La contracción de longitud de Lorentz-Einstein no existe.
La contracción de longitud y la dilatación de tiempo de Lorentz-Einstein no existen.
¿POR QUÉ LA VELOCIDAD LOCAL DE LA LUZ ES LA MISMA PARA CUALQUIER POSIBLE OBSERVADOR LOCAL?
La relativización relacional en la variación de posición es la verdadera causante de que la velocidad local de la luz sea constante para todos los observadores locales.
Las nuevas transformaciones relacionales demuestran que no hace falta ni paradójicas dilataciones temporales ni contradictorias contracciones de Lorentz para explicar la constancia local de la velocidad de la luz.
Es más, ¡pensad fácil!, la velocidad local de la luz es constante, precisamente, porque ni existen dilataciones temporales ni existen contracciones de Lorentz: Todos los observadores locales, con total independencia de sus posibles velocidades relativas, están de acuerdo en que la luz recorre la misma longitud -sin contracción- en el mismo tiempo -sin dilatación-. Su cociente es siempre la constante "c".
Las asimetrías en el uso del lenguaje ordinario relativista bastan para demostrar que la teoría de la relatividad es falsa. Pues si la relatividad se ve obligada, para intentar justificar de cualquier modo la constancia local de la velocidad lumínica, a inventar una dilatación del tiempo, ¿no debería haber también inventado, con la proporcional correspondencia simétrica que preservara dicha constancia, una dilatación de la longitud, que no contracción de Lorentz?
Ni la relatividad de la variación de posición ni una posible relatividad de la longitud consiguen que el espacio deje de ser absoluto. Las transformaciones de Lorentz-Einstein reemplazaron las transformaciones de Galileo-Newton, pero no consiguieron eliminar el espacio absoluto de Newton. Las nuevas transformaciones relacionales refutan las de Lorentz-Einstein para implantar el nuevo espacio relacional, no absoluto.
Einstein nunca supo cómo deshacerse del espacio absoluto y de los sistemas de referencia inerciales de Newton. Hizo lo contrario de lo que debería haber sabido hacer. Su principio de equivalencia empeoró todavía más las cosas de lo que ya lo estaban por culpa de las transformaciones de Lorentz. Al volver a proclamar, aunque tan sólo fuese localmente, la supuesta existencia real de los sistemas inerciales absolutos de Newton, ¡incluso en presencia de campos gravitatorios!, consiguió lo contrario de lo que debería haber conseguido. Contaminó de confuso espacio absoluto cualquier posible recóndito lugar del universo.
Todo observador, esté o no esté en caída libre gravitatoria, tiene derecho a considerarse una referencia espaciotemporal "absoluta". Referencia relacional (en esto llevaba razón Leibniz). Las ecuaciones de la nueva teoría conectada, que generalizan las ecuaciones de la nueva teoría relacional, han conseguido por fin eliminar el espacio absoluto de Newton-Einstein: la constante "c" tan sólo representa la velocidad local de la luz. La verdadera naturaleza de todas las coordenadas espaciotemporales es relacional.
Basta ya de números complejos y de tramposos cambios de sistemas de coordenadas imaginarias... 1687 pasará por fin, porque se lo merece, a la historia de la física. Ha llegado la hora de la nueva revolución copernicana. La verdadera invariancia universal de las leyes físicas. La absoluta relatividad del movimiento.
La verdad... ¿no os parece que el sol empieza a moverse...?
P.D.: Desde la sección Información del blog ‘Einstein vs Teoría Conectada' se puede acceder a todas las referencias incluidas en el presente texto.
| Este apunte fue enviado por su autor en formato DOC (Word).
Para poder visualizarlo correctamente (con imágenes, tablas, etc) haga click aquí o aquí si desea abrirla en ventana nueva. |
Comentarios de los usuarios
Agregar un comentario:
Fecha: 04/01/2012 -- Hora: 17:31:49
Autor: Ricardo - mythbusterfvc@hotmail
Asunto: Lorentz-Einstein
Mensaje: No es necesario poder entender las ecuaciones del trabajo presentado para saber que sus conclusiones son ridÃculas y expresadas con una insólita arrogancia. La dilatación temporal predicha por la Relatividad ha sido comprobada experimentalmente sin falla alguna...multitud de instrumentos funcionan asumiéndola, los GPS para nombrar sólo uno. Aquà nos pretenden demostrar que todo eso no sucede...en fin
Boletín de Novedades
Acceso rápido
• Monografias
• Examenes
• Enlaces
• Publicar material o sitio
• Foros
• Diversion
• Test de Orientacion
• Institutos
• Secundarios
• Universidades de Argentina
• Residencias Universitarias
• Guia de Carreras Universitarias y Cursos
• Cultura del Mundo
• Buscador en tu sitio
Sobre ALIPSO.COM
Monografias, Exámenes, Universidades, Terciarios, Carreras, Cursos, Donde Estudiar, Que Estudiar y más: Desde 1999 brindamos a los estudiantes y docentes un lugar para publicar contenido educativo y nutrirse del conocimiento.
Contacto »Legales