La encriptación
|
Introducción. ¿Por qué usar criptografía? Métodos criptográficos. La sustitución. Breve historia de la criptografía. Complejidad
Agregado: 06 de JULIO de 2008 (Por Ramiro Gomez) | Palabras: 2872 | Votar |
 | Promedio: 10
| Promedio: 10
Categoría: Apuntes y Monografías > Ciencia y tecnología >
Material educativo de Alipso relacionado con encriptación
Enlaces externos relacionados con encriptación
Autor: Ramiro Gomez (ramiagomez@yahoo.com.ar)
 Este apunte fue enviado por su autor en formato DOC (Word).
Para poder visualizarlo correctamente (con imágenes, tablas, etc) haga click aquí o aquí si desea abrirla en ventana nueva. Este apunte fue enviado por su autor en formato DOC (Word).
Para poder visualizarlo correctamente (con imágenes, tablas, etc) haga click aquí o aquí si desea abrirla en ventana nueva. |

Indice
Introducción ............................... 1
¿Por qué usar criptografía? ................ 2
Métodos criptográficos ..................... 3
La sustitución ............................. 4
Breve historia de la criptografía .......... 5
Complejidad ................................ 7
Palabras finales ........................... 8
Bibliografía ............................... 8
Introducción
Todos hemos oído alguna vez hablar de los hackers, ya sea en
películas, en alguna noticia, o que nos cuenta un amigo. El
propósito de los hackers se centra en la piedra filosofal de
la era actual: la era de la información.
Ha habido algunos teóricos importantes que afirman que hoy por
hoy el poder no está basado exclusivamente en el dinero, sino
en la información. Quienes tengan la información justa en el
momento preciso, serán capaces de lograr fortunas o poder, sin
límites aparentes que los restrinjan.
Imaginen poder saber con anticipación los valores que tendrán
las bolsas en el mundo, saber qué hará el enemigo, determinar
la ubicación exacta de determinada persona, saber cuál va a
ser el destino de la humanidad en el futuro. Y habría miles de
ejemplos.
Hay personas que saben determinadas cosas que la gran mayoría
desconoce. Conocimientos o información que son muy difíciles
de obtener, o caros (fórmulas químicas, fórmulas de
medicamentos, información sobre procesos industriales,
mensajes entre altos funcionarios de algún gobierno, etc.). Es
por eso que la encriptación surge para brindar métodos seguros
de comunicación, aún con el canal interceptado o el algoritmo
criptográfico obtenido.
En el caso de estas personas que tienen conocimientos o
información secretos, deben aplicar encriptación a sus
mensajes para comunicarse con otra persona sin que el mundo se
entere.
Encriptar significa traducir un mensaje o conjunto de datos a
símbolos y códigos variados que no tienen un significado
directo; es decir que cualquiera que intercepte el canal de comunicación y tenga acceso al mensaje (a la señal) no pueda entender cuál es su verdadero significado. Por ejemplo, el texto
"Peiper te ofrece white papers gratuitamente!", puede ser traducido a
"oos�;watr48%(#/$ljf#"=00r4mfsYY402:-$le%0�&�". Si alguien lee el texto encriptado no va a poder entender de qué se trata, conservando el verdadero contenido del mensaje para su destinatario original.
Claro que no es realmente necesario encriptar los mensajes para saludar a un amigo o un pariente, pero a nivel gubernamental y a veces empresarial la posesión de determinados datos o información es en extremo valiosa.
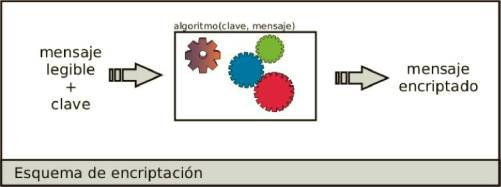
Por esta razones, en esta edición digital de Peiper vamos a hablar de la encriptación o criptografía (tomándo ésta última como la disciplina que estudia la encriptación). Como obsequio de nuestro sitio Peiper, en la sección "progs" van a encontrar un software casero desarrollado por el autor de este white, que aunque no tiene las complejidades de los algoritmos más actuales, es suficiente para resguardar nuestra información casera bajo llave. Ahora sigamos con lo nuestro!
¿Por qué usar criptografía?
Los métodos criptográficos pueden ser usados a nivel proveedor
o usuario. Tal es el caso de las empresas telefónicas que
encriptan los datos de la voz; o Internet, que dispone de una
cartera de algoritmos criptográficos para garantizar la
seguridad de la red.
Pero por otro lado, aunque la mayoría no sea capaz de obtener
los mensajes originales, sí lo puede hacer, por ej., la
empresa telefónica. Si adicionalmente le damos a nuestros
datos protección extra, ni siquiera la empresa podrá conocer
nuestro mensaje.
Como criterio de decisión para usar o no criptografía,
determinamos que si la información es muy importante y nos
puede llegar a perjudicar que otras personas no destinatarias
la lean, debemos usarla.
Si sólo enviamos saludos o cartas a amigos/as o parientes, no
tenemos motivos para usarla.
Hoy por hoy no tenemos casi necesidad de hacerlo por nosotros
mismos, ya que cuando se trata de tarjetas de crédito, cuentas
bancarias, etc. el banco o empresa nos brinda una base de
seguridad considerable.
Métodos criptográficos
Las técnicas más comunes que usa la criptografía son:
� sustitución
� trasposición
� checksums, hashing o variantes de éstas
La sustitución reemplaza un carácter o conjunto de caracteres por otro conjunto de caracteres. Matemáticamente la podemos expresar como una función que asigna a un valor x, un valor y.
Sust : N(L) → N(L+A)
Esto quiere decir que la longitud de los datos de salida (imágen) es la longitud de los de entrada más/menos un valor entero positivo A. En general, A ≈ 0. Si A < 0, estamos hablando de compresión (que en cierto sentido también es encriptación) y el mensaje encriptado reduce su longitud. Si A = 0 es problable que el mensaje se halla codificado reemplazando cada carácter por otro, posiblemente bajo un sistema criptográfico ROT.
Sust : f(x1 x2 ...) = a1 a2 ...
(con x1 x2... ≠ a1 a2 ..., long(x1) ≥ 0, long(x2) ≥ 0, long(xi) ≥ 0, long(x1) + long(x2) + ... ≥ 1)
La trasposición cambia el orden de los caracteres o conjuntos de caracteres. Usando esta técnica la longitud del mensaje encriptado es igual a la del mensaje original. Los checksums, por su parte, son valores numéricos que se obtienen de sumar todos los valores de los carácteres del mensaje. Luego de hacer esta suma, su valor se agrega al final del mensaje. Cuando se procesa el mensaje se hace nuevamente esta suma y tiene que ser igual a la anterior que está almacenada en el mensaje. Esto sirve para saber si el mensaje fue modificado ilegalmente (por ej. con un editor de texto). Para poder modificarlo y evitar que sea detectada esta acción deberíamos cambiar no sólo el mensaje sino también la suma de verificación.
Extendiendo la idea de checksum, se pueden generar otros valores computados a partir del mensaje usando hashing. Esto
daría una especie de resúmen que nos firma el mensaje de acuerdo a su contenido.
Hay que nombrar que esta técnica es muy usada en las firmas digitales, de modo que se consigue una clave privada que relaciona la clave pública con el contenido del mensaje. Métodos similares se usan en los archivos comprimidos para saber si el mensaje se preserva en estado consistente; y hasta en algunos dispositivos de almacenamiento como discos rígidos (a muy bajo nivel, implementado en hardware).
La sustitución
Vamos a hacer hincapié en esta técnica porque es la que realmente modifica el contenido del mensaje para dejarlo ilegible.
La sustitución en general se basa en problemas matemáticos complejos, muchas veces relacionados con la teoría de números: números primos, álgebra de módulo, divisiones enteras, etc. Estos problemas son ideales para encriptar ya que la operación de desencriptado consiste en resolverlos, y ésto puede tomar tiempos exponenciales. En general se usan problemas cuya solución rápida o analítica se desconoce, y la única manera de obtenerla es probando una por una.
Resolver un problema como la factorización de un número muuyy grande en sus factores primos hoy en día es complicado. No se han descubierto (mejor dicho: divulgado) algoritmos eficientes de factorización, lo que significa que debemos usar la fuerza bruta para romper claves. Usar fuerza bruta es probar con todas las posibilidades, hasta que se encuentre la correcta. Por ejemplo: si tenemos una clave (contraseña) de 32 bits (4 bytes o 4 caracteres ASCII) para probar todas las posibilidades tendremos que evaluar 2^32 claves. Esto ocurre si la correcta es justo la última (tuvimos mala suerte!). Entonces es mejor calcular la media (promedio) del total de pruebas. 2^32/2=3^31. Sigue siendo un número grande, más de 2000 millones.
|
¿Por |
qué es |
2^n? |
|
|
|
|
|
|
|
|
|
Imaginen que tenemos 1. |
4 bits, |
donde cada |
uno |
puede |
tomar un |
valor |
0 o |
|||
|
Para |
1 bit tenemos 2 |
combinaciones: 0 o |
1. |
|
|
|
|
|
||
|
Para |
2 bits |
tenemos |
4 comb.: |
00, 01, 10, |
11. |
|
|
|
|
|
|
Para |
3 bits |
tenemos |
8 comb.: |
000, 001, 010, |
011, |
100, |
101, |
110, |
111. |
|
|
Para |
4 bits |
tenemos |
16 comb. |
|
|
|
|
|
|
|
Ahora harémos una clasificación de acuerdo a la variación de
los códigos utilizados.
� sustitución simple: cada carácter se reemplaza por otro. Por ej. a -> n. La correspondencia no cambia en todo el cifrado. Un ejemplo es el sistema criptográfico ROT. Es el cifrado más inseguro, y posibilita la detección de
repeticiones de caracteres, como espacios por ej.
� sustitución en intervalos: los
caracteres se reemplazan
por otros pero se repiten cada determinado intervalo.
Por ej. a→n, b→m, ........ , a→w, b→x, ....... a→n,
b→m. Aquí vemos que la primera "a" se sustituye por la letra "n", la segunda "a" por la letra "w". Pero después de cierto intervalo, la "a" se reemplaza nuevamente por "n".
� sustitución
azarosa: cada carácter se reemplaza por uno
distinto, y no hay una ley precisa que determine los
intervalos de repetición. Por ej. a→n, b→m, .........
a→w, b→x, ......... a→1, b→2, ... Es decir que cada
carácter nunca se va a reemplazar por un mismo carácter con igual frecuencia. Es la generalización de las 2 primeras clasificaciones, siendo la más segura de todas. Además no permite detectar carácteres repetidos. Una desventaja de ésta es que es muy probable que deje al mensaje con poca capacidad de compresión, o sea que casi no lo podremos comprimir por los métodos tradicionales basados en redundancia de información. Un ejemplo es el software Seyo 2 que tiene implementados los 3 niveles. El algoritmo básico ByteXByte es el caso de sustitución simple. El algoritmo xorizador nos provee de sustitución en intervalos. Y el más seguro de todos es motorikke, que brinda sustitución azarosa. El problema de la sustitución presentado hasta aquí parece ser trivial, pero no lo es. Para desarrollar un sistema criptográfico sus creadores parten de la base de que el algoritmo de cifrado es público, se conoce. Es posible obtenerlo mediante técnicas de ingeniería inversa. Por eso el secreto no debe estar en el algoritmo, sino en la clave. Un buen algoritmo criptográfico es aquel que depende de su clave. Dependiendo de su valor, el algoritmo se comportará de una u otra manera. Así tenemos millones de algoritmos posibles que se pueden generar a partir de todas las claves posibles. Como ven, no es algo trivial; menos si se trata de cifrado asimétrico (con 2 claves, una para encriptar y otra para desencriptar).
Breve historia de la criptografía
De acuerdo a diversos documentos, la criptografía tiene sus orígenes en Grecia. Es posible que la primera persona en idear un sistema criptográfico fuera Polibio. Su sistema se basaba en sustituir las letras del mensaje por letras asociadas en una tabla. Sería el caso de sustitución simple que planteamos arriba. Otro método ideado por los griegos se denominaba escitala espartana, que consistía en un cilíndro en el que se enrollaba el mensaje y se formaban las claves de encriptación
- desencriptación.
También se le atribuye a Julio César (a cargo de la milicia
del imperio romano) uno de los primeros sistemas. Se lo puede
encontrar como algoritmo Caesar, o ROT (de rotación).
En el año 1465 el italiano Leon Battista Alberti ideó un
sistema basado en sustitución polialfabética. Esto quiere
decir que a un conjunto de carácteres de entrada con longitud
n se le asocia un conjunto de salida de longitud m. Supuso un
avance importante para la época.
En el siglo XVI el francés Blaise de Vigenere escribió un
tratado sobre la por entonces denominada "escritura secreta".
En el siglo XVII tenemos a Selenus, cuya obra es
"Cryptomenytices et Cryptographiae" (escrita en 1624).
En este mismo siglo los reyes, que por ese tiempo eran las
personas más poderosas, demostraron mucho interés en las
técnicas para hacer "códigos secretos". El rey Felipe II
encomendó a sus matemáticos hacer un sistema secreto, que
luego fue roto por el matemático Fracois Viete para el rey de
Francia.
Es curioso como en la mayoría de los casos el desarrollo de la
criptografía se relaciona con fines militares. Y lo sigue
haciendo hasta hoy.
|
|
En la 2da Guerra Mundial hubo
un avance importante en
criptografía (lamentablemente
gracias a una inútil guerra).
Los nazis diseñaron la máquina
Enigma (que vemos en la foto),
que estaba conformada por
rotores que automatizaban los
cálculos para encriptar y
desencriptar los mensajes. Para
descifrar los mensajes nazis se
convocó a los mejores
matemáticos de la época, que
fueron ayudados por máquinas
automáticas de cálculo, las
primeras computadoras.
Turing estuvo muy relacionado
con la obtención de algoritmos
de descifrado.
Avances posteriores fueron hechos en parte por Claude Shannon
con su teoría de la información. Shannon también se destacó
por sus investigaciones sobre compresión, y estableció un
límite para la compresión máxima posible llamado umbral de
Shannon.
En esta época ya se puede ver que la actividad criptográfica
estaba monopolizada por las agencias de inteligencia, en especial por algunos departamentos de Estados Unidos, el dep. de defensa por ej.
Como nos cuenta Manuel Castells en una lección inaugural:
"En Estados Unidos, la supersecreta National Security Agency (con poderes
mucho más extensos que los del FBI o la CIA) fue y es la que dispone de la
mayor capacidad tecnológica de encriptación/desciframiento del planeta. Tal
importancia se le atribuyó a esta tecnología que se clasificó en el rubro de
armamento que no se podía exportar fuera de Estados Unidos sin un permiso
especial del Departamento de Defensa.
De modo que enviar una fórmula matemática a un colega fuera de Estados Unidos
se convirtió en un delito penado por la ley. Más aún, la NSA tuvo buen
cuidado de cooptar, contratar o amenazar a aquellos matemáticos que se
adentraron en ese complejo campo de investigación. Pero hubo quienes
resistieron a la presión y se atrevieron a desarrollar fórmulas autónomas de
encriptación. Tal fue el caso del legendario Whitfield Diffie, un matemático
sin carrera académica, obsesionado por la encriptación desde joven, que, en
colaboración con un profesor de Stanford, Marty Hellman, y con la ayuda de un
estudiante de Berkeley, Ralph Merkel, descubrió, a mediados de los setenta,
nuevas formas de encriptación y, pese a las presiones del gobierno, las publicó. Su genialidad consistió en el llamado principio de la doble clave o
clave pública."
Como vemos, esta gente se lo tomó muy en serio y enviar una de estas fórmulas a un colega fuera de Estados Unidos implicaba un delito.
Posteriormente, a medida que la criptografía dejó de ser en parte un secreto de estado, se la comercializó. Se implementaron sistemas para comercio electrónico, firma digital, banca virtual, etc. La mayoría están basados en criptografía asimétrica, con una clave privada y otra pública. Hoy en día (diciembre de 2007) ya no es tan misteriosa la palabra criptografía, y hay miles de profesionales en todo el mundo especializados en ella. También hay muchos criptoanalistas, personas especializadas en descifrar los códigos secretos.
Complejidad
En general, la seguridad de un mensaje cifrado pasa por su clave. Si la sabemos hechamos por la borda todo el algoritmo de cifrado. Es por eso que muchos criptoanalistas intentan romper la clave antes que realizar un análisis de frecuencia, por ejemplo.
La longitud de las claves depende del sistema de cifrado que estemos utilizando. En los sistemas de única clave (criptografía simétrica) la longitud tiende a ser menor que en los de doble clave (crip. Asimétrica).
Una clave normal tiene una longitud de 256 bits. También tenemos valores menores como 128, 64, 32 bits, etc. Los valores mayores se consideran "imposibles" de romper. Se sabe que para claves lo suficientemente largas y uando fuerza bruta
el tiempo que se tardaría en romperlas sería mucho mayor que
la edad del Universo conocido (13000 millones de años).
Claves de 1024 bits están muy por encima de lo considerado por
los sistemas militares de todo el mundo.
Todo esto nos dice que la fuerza bruta no es la solución. De
hecho, el fuerte de la criptografía moderna está en este
punto. Para romper los códigos criptográficos tal vez sería
mejor usar los puntos débiles, que son...
Bueno, si lo supiera es probable que no estaría escribiendo
este white, no les parece?
Para finalizar, hemos comentado que se han desarrollado métodos de encriptación en extremo avanzados, algunos de los cuales anuncian ser "indestructibles". Pero nos preguntamos... ¿qué necesidad hay de proteger tanto algunos mensajes? ¿Existe información tan importante como para llegar a implementar cosas de este estilo? Y la respuesta es que no lo sé, pero sin duda el banquete debe ser grande, tan grande como para construir o derribar una nación entera...
Palabras finales
Hemos visto una rápida y jugosa introducción a la criptografía (más bien de estilo conceptual), pero nos han quedado muchas cosas por contar. No hablamos de los algoritmos actuales, ni del criptoanálisis, ni del futuro de la criptografía. Desde el sitio web "Peiper" te prometemos que habrá una segunda entrega sobre este tema. Tan sólo mantente actualizado en nuestro sitio. �Hasta la próxima!
Ramix
Bibliografía
Wikipedia: www.wikipedia.com
Textos científicos: www.textoscientificos.com
Servicio de Informática de la Universidad de Cantabria
Lección inaugural del curso académico 2001-2002 de la UOC
Manuel Castells: www.uoc.edu
Encriptación.
Recursos digitales
Esquema de encriptación: Ramix
Máquina Enigma: Wikipedia (www.wikipedia.com)
White paper perteneciente al sitio "Peiper": www.peiper.com.ar







