1 voto | Promedio: 10

LA PARADOJA DE LOS GEMELOS DE LA TEORíA DE LA RELATIVIDAD DE EINSTEIN

LA TEORíA RELACIONAL: UNA INTRODUCCIóN A LA TEORíA CONECTADA

Xavier Terri Castañé

� Del texto: B-2320-09

Xavier Terri

Barcelona, 5-5-2009

Autor: Xavier Terri Castañé

Editora: Alicia Pardo Mateo

Printed in Spain - Impreso en España por

Bubok ediciones

 

En el presente texto me limito a demostrar, libremente enfrentado a todo lo que hasta ahora se sabe, que las célebres Transformaciones de Lorentz de la Relatividad Especial no son las únicas ecuaciones que consiguen explicar la constancia de la velocidad de la luz en el vacío.

Aquí presento unas nuevas ecuaciones alternativas, las transformaciones relacionales, que son las únicas ecuaciones que son consistentes con la constancia de la velocidad de la luz en el vacío y que, a un mismo tiempo, resuelven la paradoja de los gemelos.

Es la muerte del relativismo. Yo creo...

Donde los muy inteligentísimos tan sólo alcanzan a ver informes pedruscos, Isaac Newton, el indiscutible mayor genio de toda la historia de la humanidad, descubre a orillas del inabarcable océano de la verdad, al menos de vez en cuando, redondeados guijarros.

SUMARIO

CAPíTULO 1: ¿ES UNA PARADOJA LA PARADOJA DE LOS

GEMELOS? ................................................................................. 9

1.        el método cinematográfico ...................................................... 11

2.        magnitudes invariantes ............................................................. 15

3.        la paradoja de los gemelos ....................................................... 17

4.        justificación relativista de la paradoja ................................ 18

5.        la contradicción de los gemelos ............................................. 21

CAPíTULO 2: LA MÉTRICA RELACIONAL .................................................... 29

1.        ecuaciones de transformación relacionales ........................ 31

2.        ecuaciones de transformación relacionales

tensoriales .................................................................................. 34

3.        determinación de �y �........................................................... 35

4.        transformación de la métrica relacional ............................ 37

CAPíTULO 3: LA MÉTRICA RELACIONAL TETRADIMENSIONAL ......... 41

1.        el intervalo diferencial elemental al cuadrado ............... 42

2.        ecuaciones de transformación relacionales 4-d ................. 46

3.        ecuaciones de transformación tensoriales 4-d ................... 49

4.        consistencia de la métrica relacional y las

transformaciones relacionales .............................................. 49

5.        transformación relacional de velocidades ........................ 51

6.        reescribiendo las transformaciones relacionales ............ 52

FORMULARIO .................................................................................................... 55

PARA REFLEXIONAR ....................................................................................... 56

¿ES UNA PARADOJA LA PARADOJA DE LOS GEMELOS?

Para dar cuenta de la constancia de la velocidad de la luz en el vacío en todos los referenciales en movimiento relativo rectilíneo uniforme, en 1905 Einstein rechazó las teorías de Newton y postuló la teoría de la relatividad especial. Su idea esencial consistió en sustituir las transformaciones de Galileo newtonianas por las transformaciones de Lorentz einstenianas.

El espacio y el tiempo, que, por separado, se convirtieron en magnitudes físicas relativas a la velocidad relativa, quedaron, no obstante, unificadas bajo un nuevo concepto absoluto, no relacional: el espaciotiempo de Minkowski, caracterizado por la célebre métrica "plana" de Minkowski:

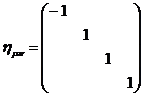(1)

Cualquier métrica presupone una definición teorética de espaciotiempo. La métrica relativista de Minkowski (1), que es matemáticamente invariante bajo las célebres transformaciones de Lorentz, presupone el espacio y el tiempo relativos a la velocidad característicos de la relatividad especial de Einstein. Además, a partir de ella, es fácil deducir la antedicha premisa: la de la constancia de la velocidad de la luz.

La predicción más espectacular, consecuencia de (1) (o de las transformaciones de Lorentz), de la teoría de 1905 de Einstein, la relatividad especial, fue la denominada dilatación del tiempo (?), que, en lenguaje ordinario, se suele expresar con la vaga proposición: �los relojes en movimiento andan más despacio', y cuya concreción relativista exacta en lenguaje matemático diferencial resulta ser:

(2)

Todos los signos son de sobras conocidos. El diferencial de tiempo �corresponde al "ente" B y el diferencial de tiempo �corresponde al "ente" A. La velocidad de B con respecto a A, , es constante, pues se considera que la relatividad especial sólo es válida para los referenciales cuyo movimiento relativo sea rectilíneo uniforme.

La dilatación relativista del tiempo (2) es consecuencia directa de las transformaciones de Lorentz einstenianas, que son las transformaciones asociadas a la métrica (1).

La doctrina relativista sostiene: la constancia de la velocidad de la luz implica apodícticamente la dilatación del tiempo, y la dilatación del tiempo implica apodícticamente la constancia de la velocidad de la luz. Esto es, ambas cosas se coimplican apodicticamente. Tal vez ¿aporéticamente?

Se presupone que la fórmula relativista de la dilatación del tiempo es compatible con la simetría según la velocidad del movimiento rectilíneo uniforme, a saber: si el ente B (referencial, o reloj, u observador, ...) se mueve con velocidad uniforme �con respecto al ente A -el cual se autoconsidera en reposo: -, entonces el ente B , en simetría cinemática con respecto de A, también tiene derecho a autoconsiderarse en reposo, , y afirmar que es en realidad el ente A el que se mueve con velocidad �con respecto a B.

La teoría de la relatividad cree que dicha simetría del movimiento requiere que la fórmula (2) permanezca matemáticamente inalterada (menos por menos es más) bajo el cambio:

(3)

La paradoja del fotón atemporal

Nótese que según la fórmula relativista de la dilatación del tiempo (2), para un ente B que se mueva a la velocidad de la luz con respecto a otro ente A (con respecto a nosotros mismos, por ejemplo), , "el tiempo se detiene": . Los relojes se detienen. Pero ¿es esto cierto? ¿Existe algún ente único que viaje a la velocidad de la luz, ? Sí. Claro que existe. Existe un único ente. La luz viaja a la velocidad de la luz. ¿Y no es acaso la frecuencia lo que caracteriza la luz? ¿No es �frecuencia' sinónimo de �reloj'? ¿No es cada fotón lumínico un luminoso ejemplo de reloj lumínico?

Las transformaciones de Lorentz, que constituyen la esencia de la relatividad especial, y que tan sólo son válidas en ausencia de gravedad y entre entes cuyo movimiento relativo sea rectilíneo uniforme, consiguieron salvaguardar la constancia de la velocidad de la luz (todos los entes con movimiento relativo rectilíneo uniforme, con total independencia de sus velocidades relativas, obtienen el mismo valor para la velocidad lumínica: la famosa constante "") a cambio de postular la naturaleza relativa del tiempo; en concreto, al precio ¿elevado? de postular el tiempo relativo a la velocidad que aparece en (2).

En lo que sigue voy a demostrar, en contra de lo que hasta ahora (no) se sabe, que las transformaciones de Lorentz einstenianas no son las únicas transformaciones posibles que consiguen salvaguardar la constancia de la velocidad de la luz. Pero antes de presentar las nuevas transformaciones capaces de conseguir también dicho objetivo, transformaciones que sólo serán válidas entre entes con movimiento relativo rectilíneo uniforme y en ausencia de gravedad (o de cualquier otra posible interacción), será conveniente introducir algunas nuevas distintas ideas.

La teoría de la relatividad especial tan sólo habla de �dilatación de tiempo' y de �contracción de longitudes'. ¿Por qué no también de �contracción de tiempo' y �dilatación de longitudes'? Esta asimetría relativista en el uso del lenguaje ordinario ¿no revelará una asimetría en la estructura lógica de la teoría misma?

EL MÉTODO CINEMATOGRÁFICO

Toda teoría de la física que admita a priori un tiempo relativo , no absoluto, también deberá admitir a priori un tiempo relacional. Y viceversa.

Imaginemos que en una divertida, pero monótona película aparece una escena en la que el protagonista -observador A- se dedica a comprobar que la velocidad de un automóvil es de 30 m/s. Si sobre la pantalla cinematográfica se está reproduciendo la película a su ritmo propio, podremos llegar a acordar con el observador A que, también para nosotros, el automóvil se desplaza a la citada velocidad. Pero si ahora doblamos, sirviéndonos del método cinematográfico conocido como cámara rápida, el ritmo de reproducción de la película, para nosotros el automóvil también habrá doblado su velocidad, los 30m/s se habrán transformado en 60 m/s. Si triplicamos el ritmo de la reproducción de la película, entonces se habrán convertido en 90 m/s; si... En general, si multiplicamos por la constante �el ritmo propio de reproducción del film, la velocidad del automóvil, así como la de cualquier otro ente que aparezca sobre la superficie de la pantalla, también quedará multiplicada por . ¿Pero cuál será la velocidad para el observador propio A, que "habita" en el interior de la película y que, tan plano como planos puedan ser los fotogramas a través de los que su mismísimo ser se sucede en el tiempo, está imposibilitado para tomar distancia con respecto a todo lo que en ella misma pueda suceder?

Es fácil de ver que para el desafortunado observador A, atrapado por el celuloide y cuyo ser no es más que una mera y monótona sucesión de fotogramas, la velocidad del automóvil no habrá variado en absoluto. La razón de ello es que para él, que está imposibilitado para escapar del interior de su propia película, se habrán mantenido internamente invariables todas las proporciones temporales. Por el contrario, para nosotros -un observador B, por ejemplo-, capaces de mirar la película a cámara rápida y desde una supuesta superioridad externa, todo lo que aparece sobre la divertida pantalla, el automóvil, los movimientos del propio protagonista, el avance de las manecillas de los relojes �el tiempo mismo!... habrá multiplicado su proceso temporal por un factor igual a la constante .

Lo rápido presupone lo lento. Por una elemental dialéctica entre opuestos simétricos, si hablamos de la cámara rápida también deberemos hablar de la cámara lenta. Si aceptamos a priori que el tiempo no es absoluto, sino relativo, entonces también deberemos aceptar que, si , el ritmo del tiempo relacional cinematográfico de A con respecto a B va a cámara rápida, y que, si , el ritmo del tiempo relacional de A con respecto a B va a cámara lenta. Existe un ritmo superior al ritmo propio y existe un ritmo inferior al ritmo propio. Una teoría de la física que no aceptara estas dos posibilidades sería tan paradójica como una moneda con cruz pero sin cara.

Sin embargo, continua siendo cierto que para el plano prisionero del celuloide el devenir de su propio tiempo ni se habrá "dilatado" ni se habrá "contraído", sino que se habrá mantenido inalterado. Para él -observador A- todas las proporciones temporales se habrán mantenido inalteradas de un modo meramente interno. Su automóvil, muy indiferente tanto a la cámara rápida como a la cámara lenta, continúa desplazándose a su ritmo propio, simbolizado, en el presente ejemplo, por los 30 m/s iniciales.

Pero ¿y si fuese cualquiera de nosotros -un observador B, por ejemplo- el que realmente estuviese atrapado, cual fotoaplanado prisionero, dentro de su propia película? ¿No tendría también el mismo derecho el observador A, desde su propia perspectiva, a decir que es él el que siempre ha permanecido habitando en su propio tiempo entre tanto que era al observador B al que, comparativamente, el tiempo le transcurría a la mitad, a un tercio,... en general, a �veces más rápido (es decir, �veces más lento) que con respecto a sí mismo?

Al observador A no le faltaría razón por un simple motivo: no existen observadores privilegiados. No existen relojes absolutos o privilegiados. Todos los observadores habitan en su propia película. Todos los entes son planos con respecto a sí mismos. Cosa que implica que todo observador, sin excepción posible, tiene derecho a considerarse a sí mismo una referencia temporal "absoluta" (la referencia "plana"). Es decir, A tiene derecho a afirmar lo que sigue: �para mí mismo el tiempo va como va, y para B el tiempo va la mitad de rápido que para mí mismo'; pero, tan "plano" como A y con igual "absoluto" derecho, B puede afirmar lo recíproco que A: �para mí mismo el tiempo va como va, y para A el tiempo va el doble de rápido que para mí mismo'. Admitir la naturaleza relativa del tiempo (el genial descubrimiento de Einstein) equivale a admitir que el tiempo puede transcurrir de distinto modo para idénticos entes, A, B, C,... que estén siendo sometidos, en diferentes grados, a estímulos físicos capaces de relativizar el fluir del tiempo.

Por tanto, el tiempo que un ente determinado, por ejemplo A, pueda asignar a otro ente idéntico, por ejemplo B, pero que esté sometido, en distinto grado que A, a estímulos físicos relativizadores del tiempo, dependerá relacionalmente tanto de B como de A. Ya que la absoluta relatividad del tiempo, la naturaleza relativa del tiempo, se manifiesta tanto a través de A como a través de B, carece de sentido hablar de �tiempo para B'. Una vez ya aceptada la einsteniana naturaleza relativa, no absoluta, del tiempo, entonces la� ciencia lógica nos obliga a expresarnos en un lenguaje que emplee proposiciones del tipo �tiempo asignado a B por A', o mejor aún, sintéticamente hablando, �tiempo para B según A', �tiempo para A según B',... Todos los observadores, todos los entes, habitan en su propia película, y cada uno de ellos es muy libre de escoger su ritmo propio como la referencia temporal propia con la que determinar, relacionalmente, las evoluciones temporales ajenas.

El ritmo propio de la película en la que habita cada ente constituye el patrón temporal "absoluto" y "localmente plano" gracias al cual dicho ente puede establecer, relacionalmente a través de él, el ritmo temporal en el que se suceden los fotogramas de cada una de las restantes películas en las que habitan el resto de los entes ajenos, cada uno de los cuales tiene a su vez idéntico derecho a considerarse a sí mismo tan "absoluto" y tan "localmente plano" como pueda pretender serlo cualquier otro posible ente.

Alcanzado este esclarecido punto, habremos de considerar una cuestión de índole meramente semiótica. Abriremos un pequeño paréntesis en las presentes explicaciones porque, antes de proseguir, será imprescindible disponer de una nítida notación sígnica que nos permita manejar con clara soltura todas estas, aunque muy simples, distintas ideas.

Imaginemos dos relojes idénticos A y B. El tiempo que tarda la secundera del reloj A en avanzar desde una división de su esfera hasta la división inmediata posterior dependerá del ritmo de reproducción de la película en la que habita el reloj A. A mayor ritmo de reproducción cinematográfica, más rápido avanzará su secundera, empleará menos tiempo. Pero el reloj B también habita en su propia película. Cuanto mayor sea el ritmo de reproducción de esta última, mayor será el tiempo que, desde la perspectiva de B, tardará la secundera de A en avanzar dicha división, empleará más tiempo. Luego, el tiempo asignado al reloj A para el avance de su manecilla desde una división determinada hasta la subsiguiente división dependerá no sólo de A, sino también de B. Esto es, dependerá relacionalmente tanto de A como de B. Luego, el tiempo asignado será un tiempo �para A según B'. Esto significa que notaciones sígnicas relativistas del siguiente tipo monádico:

, , , ,...

son incompletas. Son notaciones que no permiten representar la naturaleza relacional del tiempo absolutamente relativo. Carecen ya de todo sentido. En su lugar se deberá emplear una notación relacional diádica tal como:

(4)

que significa �tiempo para A según B'.

Nótese que esta notación no obedece a ningún capricho, pues en general es fácil de ver que: , , , ...

(En el presente caso concreto de la antedicha secundera, puesto que A y B son relojes idénticos, propiamente -es decir, cuando los entes se limitan a permanecer encerrados dentro de su propia película- se tiene que: )

La posición relativa en el medio gravitatorio como estímulo físico relativizador del tiempo

Quien haya leído mi tractatus physico-philosophicus sabrá que, según la teoría conectada, el tiempo transcurre de distinto modo en diferentes puntos del medio gravitatorio. La posición relativa en el medio gavitatorio es, pues, un estímulo físico relativizador del tiempo. Sean dos entes idénticos unos observadores que observan el tiempo. Claro está, me refiero a dos relojes idénticos, A y B. Como el fluir del tiempo depende del punto del medio en el que está ubicado cada reloj, el tiempo que según B tarda la secundera del reloj A en desplazarse desde una división de su esfera hasta la división inmediata posterior (propiamente, un segundo según A), dependerá de la posición en el medio en donde está ubicado el reloj A. Pero dicho tiempo también dependerá de la posición en donde está ubicado B, pues si el tiempo transcurre de distinto modo en diferentes puntos del medio gravitatorio, entonces dicha relativización del tiempo actuará no sólo sobre la posición de A, sino también sobre la posición de B.

En este ejemplo se aprecia muy claramente que en toda teoría que admita a priori la relatividad del tiempo, las monádicas notaciones sígnicas relativistas, por ejemplo �o , deben ser reemplazadas por notaciones relacionales diádicas: , , �y . Ulteriormente la teoría deberá ser capaz de establecer cómo se relacionan entre ellas.

¿Qué significa la fórmula relativista de la dilatación del tiempo (2)? ¿ o ? ¿Es compatible la estructura matemática de la relatividad especial con la simétrica naturaleza relacional del tiempo?

En síntesis: si queremos construir una teoría que esté dispuesta a admitir a priori la naturaleza relativa del tiempo y que, además, rechace la existencia de cualquier tipo posible de observador privilegiado o absoluto, entonces habremos de tener siempre presente que la coordenada temporal se tiene que definir a priori mediante una proposición relacional. Las proposiciones monádicas relativistas �tiempo para A', �tiempo para B',... no tienen el menor sentido en el contexto de una tal teoría. Tendremos que expresarnos con proposiciones relacionales parecidas a: �tiempo para A según B', �tiempo para B según A', �tiempo para B según C',... Y, en general, cuando intervenga cualquier ente (...) susceptible de ser tratado relacionalmente: �(...) para B según A'.

Dos relojes idénticos pero expuestos, en diferenciados grados, a estímulos físicos relativizadores del tiempo habitan en distintas películas. Para expresar correctamente la relatividad del tiempo deberemos indicar las correspondientes dos películas en donde habitan los dos relojes (obviamente, para Newton no existe ningún tipo de estímulo físico relativizador del tiempo y todos los relojes habitan en una misma película: �Tiempo absoluto').

Todo lo que se acaba de decir sobre las proporciones relacionales temporales puede también decirse con respecto a las proporciones espaciales. Un observador B podría afirmar que la imagen de la pantalla, en donde habita el observador A, se ha ampliado, o se ha reducido, �veces; pero el observador A tendría derecho a sostener, recíprocamente y con idéntico pleno derecho, que es la imagen de la pantalla en donde habita el observador B la que relacionalmente se ha ampliado, o se ha reducido, �veces. De hecho, desde dentro de nuestro pequeño "universo", atrapados en nuestra propia película, aunque las dimensiones espaciales y temporales estuviesen cambiando incesantemente, si éstas se mantuvieran relacionalmente inalteradas, nunca seríamos capaces de notar variación alguna. Un muy eminente sabio, exterior a nuestro pequeño universo, podría advertir que la imagen espacial de nuestra película se está expandiendo incesantemente a lo largo y ancho de todas sus direcciones espaciales. Podría advertir que cada día que pasa todos los entes que la habitan, incluidos nosotros mismos, están, por decir algo, doblando su tamaño incesantemente. Pero nosotros mismos, prisioneros del celuloide y tan planos como planos puedan ser los fotogramas en los que se sucede nuestro ser, seríamos incapaces de reconocerlo.

Los argumentos precedentes, no obstante, no son del todo completos. No son del todo exactos si tenemos en cuenta que pueden ser reinterpretados, en el contexto de un nivel lógico superior, como "meta-argumentos". El ser comienza a ser percibido. El ente se revela contra lo cerril; tetradimensionándose comienza a adquirir relieve sobre el plano fotograma. En efecto, cuando decimos que no podemos escapar de nuestra propia película estamos ya reconociendo, de algún modo, que existe algo más allá de nuestra propia película. Algo más allá de nuestra limitada visión, "localmente plana", de todos los entes, de los cautivos entes que se eternizan dentro de sus planos fotogramas. En realidad, estamos ya reconociendo que estamos a punto de trascender todas las teorías sobre el tiempo hasta ahora conocidas. Estamos intuyendo la esencia de lo aún por venir...

"¿'El enigma no existe'?"

¿'La lógica llena el mundo'? ¿Somos capaces de trascender �el' mundo, "entendido como un todo"? ¿Es posible que alguien tenga la facultad de escapar de �el' mundo para, cual altísima y serenísima divinidad, contemplarlo desde una supuesta no antinómica exterioridad? ¿Es posible descubrir una expansión del universo desde dentro del propio universo? ¿Acaso no son falsas las ecuaciones que proporcionan el sustento teorético -las Ecuaciones de Einstein- a los orígenes absolutos de �el' tiempo y a las teorías bigbangvescas? ¿No será la "teoría" del big bang el mayor fraude intelectual del pasado siglo? ¿No serán ciertos sectores de la ciencia oficial actual los prepotentes canalizadores del mismo tipo de energúmenos que antaño vociferaban en nombre de lo Absoluto? ¿Tan prestas aguardan las llamas?

¿No, no,no,no sí, sí sí, sí? ¿(...)? Luego ¿(...)?, ..., ¿(...)?, ..., ...infinitamente etcétera...

Dados tres entes A, B y C, la naturaleza relacional del tiempo implica que éstos se relacionan mediante la siguiente trivialidad (trivialidad que la teoría de la relatividad es incapaz de entender):

Si �entonces (5)

Es decir, si un proceso cualquiera C, al cual sempiternamente le place ocupar una cierta "esfera temporal" (es decir, para que todos nos entendamos y todas las inteligencias congenien entre sí, un ente al que le place hacer tic-tac, tic-tac, tic-tac,...), transcurre �veces más rápido según A que según B, entonces transcurre �veces más rápido según B que según A. Lo mismo puede decirse con respecto a las proporciones espaciales.

Para expresar las tetracoordenadas relacionales diferenciales espaciotemporales para B según A emplearemos la siguiente notación:

(6)

donde el superíndice tensorial �puede tomar los cuatro valores 0 (índice temporal), 1, 2 y 3 (índices espaciales).

MAGNITUDES INVARIANTES

Aun con el riesgo de llevarla demasiado lejos, pero con la esperanza de que ayude al inteligente lector a alcanzar cierta esencia de lo aún por venir, si seguimos con la anterior metonimia cinematográfica observaremos que toda película tiene ciertas propiedades intrínsecas con las que todos los observadores congenian y están de común acuerdo.

Un avisado observador exterior B puede considerar que, para él, la velocidad del anterior automóvil es de 60 m/s, el doble de la velocidad que mide el observador plano A que habita dentro de su propia película. Pero B, consciente del método cinematográfico de la física, podrá averiguar de algún modo que, para A, la velocidad del automóvil continúa siendo de 30 m/s . De forma parecida, el observador B puede considerar, por decir algún número, que la longitud del automóvil es de 12 metros, entre tanto que para el observador A tal longitud es de 4 metros. Pero esta aparente discrepancia entre A y B también tiene una explicación. La razón es la misma de antes: la unidad de medida, el metro, es para A propiamente 1 metro, pero, para B, que ve una película fotográficamente ampliada, este metro se ha convertido en 3 metros, de tal modo que B es capaz de inferir que, para A, se han mantenido inalteradas las proporciones espaciales (12:3=4). Así, aunque para B la longitud real del automóvil es de 12 metros, B también es capaz de averiguar, trascendiendo su propia película, que la longitud del automóvil A que aparece en la película A es de 4 metros para el ente A.

Con total independencia del ritmo de reproducción de la película o de si cada uno de sus fotogramas está ampliado o reducido fotográficamente, la película posee ciertas propiedades intrínsecas que son comunes -invariantes- para todos los observadores posibles. Tales propiedades son las que mediría directamente un observador "plano" que habitara dentro de los fotogramas de la propia película, pero que, indirectamente, también pueden llegar a ser conocidas o deducidas por el resto de los observadores externos a dicha película.

Desde un punto de vista lógico, la clase de las proposiciones relacionales �(...) para B según A' contienen la subclase de las proposiciones autorreferentes �(...) para A según A' o �(...) para B según B'. Estas últimas son las proposiciones propias que permiten expresar las magnitudes invariantes de la película. Son las proposiciones que permiten resaltar todas las propiedades intrínsecas de la propia película, propiedades en las que todos los observadores posibles convergen. Aunque diferentes observadores externos puedan asignar, por supuesto, con idéntico pleno derecho, diferentes longitudes reales al automóvil A de la película A que la longitud que le asigna el propio ente A, todos coincidirán en que la longitud propia de este automóvil, �la longitud para A según A', es siempre de 4 metros. La longitud propia es, pues, un ejemplo de magnitud invariante.

Como más adelante tendremos ocasión de comprobar, la métrica también tiene, al igual que las tetracoordenadas, una naturaleza relacional. Es, en general, una métrica �para B según A'. Esto significa que, en particular, podrá ser reducida a una métrica propia �para A según A'. Esta métrica propia, tan particular e incapaz de trascender su propia película, no es otra cosa que la relativista métrica plana de Minkowski (1).

�Demostrado!: la velocidad local de la luz es siempre igual a "c"

Lo expresado en el presente subtítulo es válido para cualquier teoría tetradimensional que no admita observadores privilegiados. En acuerdo con el principio de conexión (ver Tractatus physico-philosophicus) todo observador, sin excepción posible, tiene derecho a considerarse una referencia espaciotemporal absoluta, es decir, tiene derecho a considerar que su métrica propia coincide con la métrica plana de Minkowski (1). Como más adelante tendremos ocasión de comprobar, la métrica relacional local de un fotón con respecto a cualquier observador es proporcional a la de Minkowski. Y, como se sabe, a partir de cualquier métrica que sea proporcional a la métrica de Minkowski se deduce que la velocidad de la luz en el vacío es igual a la constante "". Por tanto, en acuerdo con el principio de conexión, para todo observador la velocidad local de la luz es siempre igual a "". Cosa que, incluso suponiendo una ausencia total de gravedad, implica la siguiente alternativa lógica: para todo observador la velocidad no local de la luz puede no ser igual -luego puede ser mayor o menor- que "" (ver El fin del espacio-tiempo roto).

Aún todavía persisto. En acuerdo con el principio de conexión, es decir, en acuerdo con la invariancia universal de las leyes físicas, el movimiento es absolutamente relativo. Cosa que implica, como más adelante el propio lector tendrá ocasión de comprobar mediante un muy sencillo cálculo, lo siguiente: no existe ninguna cota máxima insuperable para las velocidades reales de la naturaleza.

LA PARADOJA DE LOS GEMELOS

Aunque no antinómica, aporía es. Pero toda aporía es consecuencia de la finita inteligencia.

La fórmula de la dilatación del tiempo relativista (2), según la cual "los relojes en movimiento andan más despacio", es tan sólo función de la velocidad relativa entre A y B. Además, la relatividad especial presupone y sobreentiende la simetría según la velocidad del movimiento relativo rectilíneo uniforme, (3), aunque, en rigor, jamás se ha conseguido demostrar que las consecuencias que se derivan de la fórmula relativista de la dilatación del tiempo, a pesar de las apariencias, sean compatibles con dicha sobreentendida simetría (véase para reflexionar: �la paradoja cinética').

Sean dos gemelos A y B. El gemelo A se autoconsidera en reposo, , y observa que B inicia un largo viaje interestelar con una muy veloz y muy galáctica nave espacial. Al cabo de un determinado tiempo, B alcanza una muy lejana estrella y, después de un rápido viraje, emprende el camino de regreso hacia el punto de partida, donde de nuevo se reúne con A. El gemelo A cree que el tiempo es relativo a la velocidad según el modo concreto que dictamina la relativista fórmula (2). A cree que "los relojes en movimiento andan más despacio" y, en consecuencia, cree que a B, por ser B el que ha estado en movimiento, el tiempo le ha transcurrido más despacio que a sí mismo. Así, con la ayuda de la citada fórmula, calcula que B ha envejecido, por decir algo, a un ritmo 25 veces menor. Cree, comparativamente hablando, que a B tan sólo le han transcurrido 2 años escasos desde que partió de viaje hasta el momento de su regreso, mientras que a él mismo, el gemelo A, le han transcurrido 50 largos años. Hasta aquí, para quien esté acostumbrado a la idea de la relatividad cinemática del tiempo, no parece (aunque sólo lo parece) que de momento haya nada extraño que discutir.

Pero hay un inconveniente. El gemelo B también conoce la fórmula (2). Y en virtud de la simetría según la velocidad del movimiento (3), es B el que se considera a sí mismo en reposo, , mientras que interpreta que es A el que en realidad partió de viaje. Según B, es A el que ha estado en movimiento. Luego, simétricamente, B calcula lo mismo y lo contrario que A. Calcula que a sí mismo le han transcurrido 50 largos años mientras que a A tan sólo le han transcurrido 2 escasos años desde que partió de viaje hasta el momento de su regreso al punto de partida, punto donde A y B se reúnen de nuevo, el mismo punto donde siempre ha permanecido B en espléndido reposo con respecto a sí mismo. ¿Cuál de los dos gemelos es el que realmente ha envejecido menos durante el transcurso del recíprocamente excluyente viaje? Esta historia, tan "simétricamente contraria" resume lo que en relatividad especial se conoce como la �paradoja de los gemelos'.

En principio, aún de un modo precipitado, parece que podríamos trivialmente eliminar la paradoja de los gemelos (suponiendo, de momento, que se trate de una verdadera paradoja) afirmando que para ambos gemelos ha transcurrido exactamente el mismo tiempo. Afirmando, pues, que ambos gemelos han envejecido exactamente lo mismo desde que se separaron hasta que volvieron a coincidir en el mismo punto. Si se consigue que ambos estén de acuerdo en cuanto al cálculo del tiempo -¿cuánto tiempo? ¿2 o 50 años, o cualquier otro número arbitrario de años?- y que este tiempo sea común para ambos, entonces no parece que tenga ya sentido hablar de paradoja alguna. Desaparece la mutua discrepancia temporal, y con ello desaparece también la posibilidad de que la paradoja se convierta en una inoportuna e insidiosa contradicción.

Pero negar dicha discrepancia temporal equivaldría a refutar la expresión relativista de la dilatación del tiempo (2) en la que ambos gemelos han confiado a la hora de realizar sus anteriores cálculos, fórmula que sostiene que el tiempo transcurre de distinto modo para entes con una velocidad relativa no nula, es decir, para entes que se estén moviendo el uno con respecto al otro o el otro con respecto al uno. Y puesto que esta fórmula es, como muy bien se sabe, consecuencia directa de las transformaciones de Lorentz (o de la métrica de Minkowski), entonces, por modus tollens, se deduce que: refutar la fórmula relativista de la dilatación del tiempo (2) equivale a refutar las transformaciones de Lorentz (y, con ello, la métrica de Minkowski). Con lo cual, al refutar estas últimas, también estaríamos refutando la premisa -consecuencia de las transformaciones de Lorentz- de la constancia de la velocidad de la luz en el vacío, premisa que no parece que pueda ser refutada a no ser que pretendamos regresar de nuevo a las insostenibles tesis newtonianas. Sería absurdo, esto está claro, regresar a Newton, pero todo parece indicar que, a partir de aquí, Einstein empezará a divagar entre graves apuros.

Todo parece indicar que Einstein ha querido atraparnos dentro de un insoluble laberinto aporético: si mantenemos la premisa relativista de la constancia de la velocidad de la luz, entonces se deduce (2), generándose la paradoja de los gemelos. Pero si solucionamos la paradoja de los gemelos del modo que aquí se acaba de exponer (negando lo que (2) afirma), entonces estaremos negando la premisa de la constancia de la velocidad de la luz. No hace falta decir que es esta última premisa la que los defensores de la relatividad mantienen como una premisa inquebrantablemente absoluta. Pero luego... ahí está, insultante, la paradoja de los gemelos: para los relativistas la fórmula (2) es también una fórmula absolutamente inquebrantable. Por lo visto, al contrario que el asno de Buridan, ciertos dogmáticos nunca dudan: comen y beben y beben y comen. Al final, agotados ya todos sus recursos, acaso acabarán, al igual que le ocurrió al pobre asno, muriendo de sed y de hambre y de hambre y de sed.

Sobra también decir, porque tampoco hace falta decirlo, que la opción elegida por los relativistas, los que defienden la teoría de la relatividad a capa y espada, es absolutamente coherente: los relativistas niegan que la paradoja de los gemelos sea una paradoja. Los defensores de la relatividad niegan que la paradoja de los gemelos implique ninguna insidiosa e inoportuna contradicción.

(Aunque en estos precisos momentos al lector tal vez aún le parezca imposible, más adelante demostraré que es posible solucionar la paradoja de los gemelos sin negar ni la naturaleza relativa del tiempo ni la premisa de la constancia de la velocidad de la luz. Lo demostraré a medida que vayamos construyendo lo que he denominado teoría relacional. Teoría especial, tan sólo aplicable para entes con movimiento relativo rectilíneo uniforme, que nos ayudará a comprender mejor la emergente esencia de lo aún por venir: la nueva teoría conectada.)

JUSTIFICACIóN RELATIVISTA DE LA PARADOJA

¿Cuál es, pues, la solución diseñada por los relativistas? ¿Una paradoja no es una paradoja? ¿La relatividad especial es una teoría no contradictoria que da lugar a contradicciones? Si no es no es, si sí es...

La solución que los relativistas ofrecen a la paradoja de los gemelos consiste en romper la simetría de la presente historia acerca de los gemelos A y B, de tal modo que tenga pleno sentido afirmar, sin contradicción y sin necesidad alguna de refutar la fórmula (2), que a los gemelos el tiempo les puede haber transcurrido, ya que han vivido historias dispares, de distinto modo. Los defensores a ultranza de la relatividad argumentan que A y B no han experimentado situaciones en absoluto simétricas. Y, en efecto, así es: el gemelo A permaneció en tierra (por citar algún lugar) mientras el gemelo B emprendía un muy veloz viaje en su muy galáctica nave espacial. Cosa que implica, y con ello se rompe la aparente simetría entre A y B, que el gemelo B habrá experimentado durante el transcurso de su largo viaje, a diferencia del gemelo A, aceleraciones y desaceleraciones. Fuerzas de aceleración al inicio de su viaje hacia la muy lejana estrella y fuerzas de desaceleración, para detener su nave, justo antes de alcanzar la muy lejana estrella. Fuerzas de aceleración al inicio de su viaje de regreso desde la muy lejana estrella hacia el punto de partida inicial y fuerzas de desaceleración, para detener su nave, justo antes de llegar al punto de partida inicial y reunirse de nuevo con A (si no existieran ni la tierra ni la lejana estrella, si sólo existieran A y B, ¿con respecto a qué estaría acelerado B? ¿y A?).

Expresado en el lenguaje -ciertamente cargado de viejas reminiscencias newtonianas- de los futuristas relativistas, el gemelo A es un observador inercial y el gemelo B es un observador no-inercial. Por lo visto, con total independencia de cuál pueda haber sido la duración total -tal vez ínfima comparada con la duración total del viaje- de los susodichos períodos de aceleración y desaceleración, a los relativistas les parece que los gemelos A y B han gozado de distintos privilegios e infortunios. A y B aparecen como opuestos dialécticos, uno es inercial y el otro es no-inercial. Es de este modo, con el uso de un irreconciliable abismo dialéctico entre opuestos contrariados, como los relativistas creen que han conseguido "romper la simetría" a favor ¿arbitrariamente? de este último: es al afortunado gemelo no-inercial B al que, comparativamente hablando, el tiempo le ha transcurrido más despacio. Veredicto asimétrico y unidireccional de la supersimétrica teoría relativista: 2 años para B y 50 años para A.

Ahora bien, lo que los contrariados relativistas parece que han logrado solucionar con el uso de (in)ciertos conceptos (e) y (in)ciertas proposiciones del lenguaje ordinario (disimulados bajo una cierta estética que a veces parece más propia de Star Treck que de las grandes obras clásicas -mi Tractatus, por ejemplo-, al final han regresado a los antitéticos conceptos �inercial' y �no-inercial' newtonianos), no parece que de veras hayan logrado solucionarlo con el uso del lenguaje matemático. El logos es uno: si un problema ha sido verdaderamente resuelto con el uso de algún tipo de lenguaje particular, entonces también deberá poder ser resuelto con el uso de cualquier otro posible tipo de lenguaje. Nunca podrá abrirse ningún abismo infranqueable entre distintos tipos de lenguaje cuando todos ellos han sido usados para expresar una misma verdad.

Prometo que lo he intentado -y ruego al lector que también lo intente-, pero, por mucho que me mire y remire la fórmula (2), me resulta imposible descifrar en ella nada que tenga que ver con aceleraciones o desaceleraciones, con fuerzas de aceleración o con fuerzas de desaceleración, con gemelos inerciales o no-inerciales, ...(a propósito, si se supone la simetría según la velocidad del movimiento rectilíneo ¿por qué no también la simetría según la aceleración del movimiento rectilíneo? ¿Es la relatividad compatible con estas dos simetrías de la cinemática pura?). Una fórmula, muy cierto es, puede depender en principio de muchísimas variables. En concreto podría depender ¿por qué no? de variables físicas tales como la aceleración, la fuerza de aceleración o de desaceleración, ... , la temperatura, la entropía, ... �Hasta podría depender, suponiendo que los gemelos A y B no sean calvos, del número de cabellos de sus respectivos cráneos! Si se diese el caso de que tales variables operasen sobre A y B en distinto grado, entonces, tal vez, podríamos encontrar alguna manera de justificar la inoportuna paradoja de los gemelos.

Pero, insisto y persisto, por mucho que examine la fórmula (2) -y ruego al lector que también la examine bien-, lo único que en ella soy capaz de constatar es que lo que en su matemático lenguaje se expresa no es más que es una sencilla relación algebraica entre sendos tiempos, el de A y el de B, que únicamente está escrita en función de la velocidad relativa entre A y B; la velocidad de A con respecto a B o la velocidad de B con respecto a A ("" es una mera constante). En la relativista fórmula (2) tan sólo soy capaz de ver una muy sencilla relación entre sendos tiempos que tan sólo depende de -y está caracterizada y determinada por- la velocidad relativa , y de por nada más. De nada más depende. Por nada más está caracterizada o determinada. Luego, ya que se presupone la simetría según la velocidad del movimiento (3) y en la fórmula (2) la velocidad aparece elevada al cuadrado (menos por menos es más), no veo ningún modo matemático posible de justificar la antedicha rotura de la simetría entre A y B que, con el uso de un obsoleto lenguaje newtonianorelativista, argumentan los defensores a ultranza de la teoría de la relatividad al objeto de rápidamente desprenderse, con tan antitética impaciencia, de la tan recalcitrante, tonta, insidiosa, estúpida e inoportuna paradoja.

Tanto A como B tienen idéntico derecho a considerarse a sí mismos en reposo, y lo único que simultáneamente dicen la fórmula (2) y su fórmula "simétrica" según la simetría del movimiento (3), obtenida al hacer en (2) la permuta de las "etiquetas" A y B, es lo que sigue: según A, B ha envejecido menos que A, y según B, A ha envejecido menos que B. Y lo que en el claro y nítido lenguaje formal de la matemática es contradictorio, es contradictorio en cualquier otro tipo posible lenguaje: ¿una paradoja no es una paradoja?

Tranquilos. Nada pasa no. Al fin y al cabo ¿no es el absurdo principio de contradicción aristotélico un principio anticuado y metafísico?

�Que lo general reniegue lo especial!

La relatividad especial no la entiende ni Dios. Nunca un confundido se confunde. Los aturdidos relativistas, cuando ya empiezan a ahogarse entre los graves apuros que provoca la relatividad especial, suelen invocar a Einstein y a su omnisciente teoría de la relatividad general. Sublime teoría, tan sólo apta para los muy inteligentísimos serenísimos, que los no iniciados, al igual que nos ocurre con aquélla, tampoco somos capaces de comprender.

Puesto que intervienen aceleraciones, la solución correcta a la paradoja de los gemelos está relacionada con el problema del ascensor "acelerado" de Einstein. Problema que, como ya expliqué en mi Tractatus, la relatividad general es incapaz de solucionar. Según esta teoría, el movimiento de una partícula libre con respecto del ascensor acelerado viene dado por unas ecuaciones de movimiento que se denominan geodésicas. Según éstas, la aceleración queda determinada por las derivadas de las componentes de la métrica con respecto a las coordenadas. Pero ¿qué es lo que hay que hacer para determinar dicha métrica? Según la relatividad general, una vez conocidas las fuentes gravitatorias, la métrica queda absolutamente determinada, sin flexibilidad alguna posible, por las Ecuaciones de Einstein de campo. Pero suponiendo, tal como es el caso del ascensor "acelerado", una total ausencia de fuentes gravitatorias, ¿qué es lo que hay que hacer para determinar la métrica?

Por otro lado, ¿a qué viene esa inflexibilidad? ¿No podría acaso el ascensor -o el autobús, o la nave espacial, o lo que sea- estar "acelerado" de un modo arbitrario? ¿Cómo soluciona la relatividad general el movimiento de una partícula libre con respecto al ascensor acelerado de Einstein? ¿Supongo que no será asegurando, al igual que ya lo hacía Newton, que el ascensor es un sistema no-inercial? ¿O, tal vez, con el uso de "tetrafuerzas ficticias de Minkowski? ¿Sí? �Bien! ��Regresad a Newton!

Entre tanto que provoca una escamada abismática inquietud, es fascinantemente fascinante comprobar cómo la relatividad general es la teoría idónea para colaborar en las mayores proezas metafísicas -el descubrimiento del origen de �el' tiempo, el sublime origen del universo todo-, y, sin embargo, no tiene ni la menor idea de cómo resolver el movimiento de un pasajero que esté viajando en un autobús "acelerado".¿No será que la relatividad aún está contaminada -insisto y persisto- por la arcaica dicotomía inercial-no inercial newtoniana?

Los verdaderos problemas nunca son los grandes enigmas. Para hallar la solución correcta a todo este tipo de problemas en los que intervienen aceleraciones relativas, hay que acudir a la nueva teoría conectada. Las ecuaciones de campo de la teoría conectada contienen una función escalar �-que nada tiene que ver con la galáctica, absurda e inflexible constante cosmológica relativista �- que resulta ser la clave para conseguir ajustar las aceleraciones relativas entre los diversos entes.

�Bien! Ya que estamos tan emparadojados, paradójicamente concedamos que la relatividad especial ha conseguido solucionar la paradoja de los gemelos. Concedamos, a pesar de todo, que la teoría de la relatividad ha conseguido demostrar matemáticamente (?) que es el gemelo B el que menos ha envejecido, resolviéndose, con el antitético y asimétrico método que se acaba de comentar, la estúpida paradoja, generada por ella misma, de los gemelos. Lo que de ningún modo se podrá acatar es que haya también solucionado el caso que a continuación se expondrá. Caso que añadirá una reveladora variante -ausencia de aceleraciones relativas- a la precedente historia acerca de la paradoja de los gemelos. Lo conoceremos como: la contradicción de los gemelos.

LA CONTRADICCIóN DE LOS GEMELOS

Dos entes A y B, o dos entes B y A, mantienen una relación perfectamente simétrica. A dice: �soy hermano de B'. Entonces, en perfecta simetría, B dice: �soy hermano de A'. A dice: �mi edad duplica la de B'. Secnotne, simetría perfecta en también, B dice: �mi edad duplica la de A'.

Imaginemos dos entes gemelos A y B que, desde una determinada distancia inicial por ambos bien conocida, se están aproximando mutuamente en movimiento relativo rectilíneo uniforme, en sentido opuesto y con la misma celeridad constante con respecto a la carretera (por tanto, sea la que sea, la celeridad relativa de B con respecto a A es la misma que la de A con respecto a B). Aunque podrían serlo, no es necesario que los gemelos A y B sean gemelos, incluso podrían ser simples colegas de diferentes edades. Aunque podría serlo, no es necesario que dicha distancia inicial sea astronómica, un colega puede partir de Girona y el otro de Barcelona. Tampoco es necesario que viajen en muy veloces naves espaciales interestelares, tan galácticas. Pueden viajar en sendos coches convencionales, algo lentos incluso. Supongamos que ahora, en este preciso instante, sus respectivos relojes, que son idénticos, están sincronizados (una forma de sincronizarlos, teniendo en cuenta que la celeridad de cada ente con respecto a la carretera es la misma, consistiría en que un tercer ente situado en el punto medio de dicha carretera lanzara sendas señales simultáneas hacia A y B para "poner a cero" sus relojes).

El ente A se autoconsidera en reposo mientras observa que B se le aproxima a una cierta celeridad, no necesariamente elevada y siempre constante. Recíprocamente, desde el punto de vista de B, es él el que, con idéntico derecho al de A, tiene derecho a considerarse en reposo. Por tanto, el ente B se autoconsidera en reposo mientras observa que A se le aproxima a una cierta celeridad, simétricamente la misma celeridad que antes A observaba sobre B. Ya que el tiempo es relativo a la celeridad relativa, puesto que "los relojes en movimiento andan más despacio", ¿cuál de los dos entes es el que menos habrá envejecido desde el inicio del viaje hasta que se crucen en el mismo punto de la carretera? (La verdad es simple. Supongo que el lector ya sabe la respuesta acertada. Pero aún debe ser usted cauto y no precipitarse, pues aún nos las habemos con los demasiado inteligentes -retorcidos- argumentos del relativismo. No obstante, sugiero al lector que retenga esa lógica respuesta en su mente para que así, a lo largo de las próximas páginas, pueda ir verificando que, desde luego, se trata de la respuesta acertada.)

A y B, o B y A, son (casi) unos ignorantes del todo: aunque ya conocen las teorías de Newton, teorías que ellos respetan y admiran, ignoran la moderna teoría de la relatividad especial de Einstein. No obstante, a semejantes entes, se les ocurre hacer un sencillo experimento: medir la velocidad de un rayo de luz -de un fotón- en el vacío. Así, tras varios ensayos, consiguen comprobar que el resultado de tal experimento acaba siendo siempre el mismo. Tal experimento siempre reproduce el mismo, para ellos, inesperado resultado: con total independencia de su celeridad relativa, los dos entes siempre obtienen un valor idéntico para la velocidad (módulo) del rayo de luz: la constante c=300.000 km/s. �Sorpresa! �Para sumar las velocidades no hay que sumar las velocidades! Un fotón, con total independencia de si lo "perseguimos" o nos "alejamos" de él, siempre nos ofrece la misma velocidad. Si nos alejamos de él, por ejemplo, a 100 km/h= 0,028 km/s, el "sentido común" parece indicarnos que su velocidad total con respecto a nosotros se obtendrá a partir de una simple suma: (c+0,028) km/s. Sin embargo, A y B acaban de comprobar experimentalmente que, de hecho, nunca ocurre así: el módulo de la velocidad -celeridad- de un fotón nunca admite "sumas" y resulta ser siempre igual a "c". A raíz de este preciso experimento y a pesar de la evidente imposibilidad de conciliar el resultado obtenido con sus caras teorías de Newton, acaban por convencerse de la veracidad de la premisa que afirma que la celeridad de la luz es constante para todos los observadores -como es el caso de A y B- cuyo movimiento relativo sea rectilíneo uniforme.

Tal premisa es sorprendente. Desagradable y molesta. Contradice la ley de la suma de velocidades newtoniana. Contradice, inoportuna e insidiosamente, las únicas y caras teorías que hasta ahora ellos conocen, las teorías de Newton. Pero por rarísima fortuna, tanto A como B no son extrañas antinomias metafísicas que están de efímero paso por este mundo, contemplando cómo los altísimos pedruscos caen hacia arriba desde más arriba pero directos hacia sus pétreos y telúricos cráneos. Son entes independientes e inteligentes, elevados espíritus inspirados por la eterna búsqueda de la verdad. No tienen el menor reparo -es más, creen incluso que es su libre obligación ética- en refutar una teoría si ésta se descubre falsa o absurda. Son filosóficos seres. No les preocupa que por mirar hacia las distantes y tan altas estrellas, sin ni siquiera darse cuenta de lo que discurre por debajo de sus mismísimos pies, puedan tropezar con algún pedrusco y caer dentro de cualquier tramposo pozo que les aceche desde cualquier inesperado lugar del camino. Anteponen la verdad a sus propios intereses. Deciden, aun a su pesar, refutar las únicas teorías que hasta ahora ellos conocen, las muy geniales e intocables teorías de Newton. Pero a la par, conscientes de su socrática ignorancia, se disponen a buscar y crear alguna nueva verdad. De hecho no les queda otra alternativa. Están obligados a construir una nueva teoría que sepa "sumar" velocidades y que sea consistente con la tan sorprendente premisa acerca de la constancia de la velocidad lumínica.

B y A, o A y B, son alquimistas de espíritu. No les importa la materia, sino las leyes que la rigen. Con esfuerzo, con un poco de matemáticas y un algo de física, con unos cuantos gramos de inmaterial filosofía y con una pizca de lógica que se evapora, con muchas gotas de genialidad, consiguen reinventar la teoría de la relatividad especial de Einstein. Crean así, superando las teorías newtonianas, la teoría de la relatividad especial de Einstein.

Es de este modo, con su tetradimensional y flamante minkowskiniana nueva teoría, como consiguen explicar la inesperada constancia de la velocidad lumínica. Al precio ¿elevado? de postular una nueva conceptualización del tiempo: un nuevo tiempo que reemplaza al viejo tiempo absoluto newtoniano y que ahora resulta ser relativo a la velocidad. En concreto, relativo a la velocidad tal cual lo dictamina la fórmula (2). Así pues, A y B ya conocen ahora todas las principales fórmulas relativistas: las transformaciones de Lorentz, la métrica tetradimensional de Minkowski,... y la susodicha fórmula relativista de la dilatación del tiempo (2).

A y B, o B y A, críticos cartesianos falsacionistas, creen que es bueno dudar, por perfecta que parezca, de cualquier intocable teoría. Deciden, pues, someter a prueba incluso a su propia teoría (que al fin y al cabo es una teoría muy limitada: no es aplicable entre entes acelerados ni para entes que gravitan). En concreto, quieren constatar la hipotética veracidad de la relativista fórmula (2) sobre la dilatación del tiempo, según la cual, expresado vagamente en lenguaje ordinario, "los relojes en movimiento andan más despacio". Por todo ello, cuando al cabo de un rato se cruzan en el punto medio de la carretera que une los respectivos orígenes, Barcelona y Girona, desde los cuales partieron A y B, A predice, con el uso de la citada fórmula, que el reloj en movimiento de B ha retrasado 7 diezmilmillonésimas de milmillonésimas de micronanosegundo con relación al suyo. Según A, él ha permanecido siempre en reposo mientras B se movía hacia su encuentro, acercándosele a determinada celeridad constante. Por simetría, B predice lo muy idéntico que A y lo muy al revés que A. Lo mismo y lo contrario. Según B, es él el que siempre ha permanecido en reposo entre tanto que A se estaba moviendo hacia su encuentro. Por tanto, según B, es el reloj en movimiento de A el que en realidad ha retrasado 7 diezmilmillonésimas de... �A pesar de que disponen de la misma teoría no consiguen ponerse de acuerdo!

¿Cuál de los dos es el que menos ha envejecido? De los dos tiempos distintos, no iguales, que reclama la monádica fórmula relativista (2) ¿cuál es el que se corresponde con A y cuál es el que se corresponde con B? El ente A dice: �Yo estoy en reposo y es B el que se mueve' y �B ha envejecido menos que yo'. El ente B dice: �Yo estoy en reposo y es A el que se mueve' y �A ha envejecido menos que yo'. �Lo contrario y lo mismo! La contradicción resulta mismamente evidente. Pero nada hay en el presente ejemplo, ninguna excusa relativista posible, que permita romper la simetría éntica entre A y B. La anterior justificación -¿"solución" acaso?- relativista a la �paradoja de los gemelos' no es aplicable al presente caso de la �contradicción de los gemelos'. En virtud de la simetría según la velocidad del movimiento rectilíneo uniforme (3), es imposible que ambos entes a la vez puedan tener razón en cuanto a cuál de los dos es el que asimétricamente ha salido "favorecido" por la relatividad cinemática del tiempo. Tal vez, ya que no se desplazan en galácticas naves espaciales y su velocidad relativa es pequeña comparada con la de la luz, tan sólo discutan por culpa de unas irrisorias 7 diezmilmillonésimas de milmillonésimas de micronanosegundo, pero basta un infinitésimo intervalo de tiempo de discrepancia para que la contradicción resulte infinita. Absoluta y total. No hay "contradicciones infinitésimas", algo es contradictorio o no lo es.

Por todo ello, la respuesta acertada a la anterior pregunta �¿cuál de los dos entes es el que habrá envejecido menos desde el inicio del viaje hasta que se han cruzado en el mismo punto de la carretera?' es, desde luego, la que el lector de las acertadas respuestas aún retiene en su mente: ninguno de los dos. �El tiempo ha transcurrido exactamente igual para ambos! Muy cierto es que a veces pueden existir varias maneras de detectar diferentes tipos de asimetrías en estructuras argumentales aparentemente equilibradas, pero en esta presente historia la simetría entre A y B es infinita. Total y absoluta. Ninguno de los dos entes ha gozado de privilegio alguno. Es del todo imposible hallar ningún tipo de asimetría en la presente historia que permita justificar unidireccionalmente la dilatación del tiempo relativista (2).

La única posibilidad lógica que queda para eliminar la presente contradicción de los gemelos es afirmar, digan lo que quiera el relativismo y la fórmula (2), que para ambos "gemelos" ha transcurrido exactamente, sin duda alguna posible, el mismo tiempo (cosa que, continúo insistiendo, no equivale a negar la naturaleza relativa del tiempo, pues asumir a priori la naturaleza relacional de la coordenada temporal equivale a asumir a priori la absoluta relatividad del tiempo. Pero sobre lo que no puede quedar ninguna duda es que en el presente caso en concreto el tiempo relacional para B según A tiene que ser exactamente el mismo que el tiempo relacional para A según B).

A y B son ignorantes del todo pero no del todo ignorantes. Son entes filosóficos, inteligentes e independientes. Son entes que son seres (en todos los sentidos posibles de �seres'). Por rarísima fortuna, a diferencia de los antinómicos sabelotodo relativistas, no tienen el menor reparo en refutar una teoría si ésta se descubre absurda o falsa. Antes ya habían refutado, a pesar de ser su más caro genio, a Newton. Antes ya habían descubierto, aun a su enorme pesar, que las caras teorías de Newton ya no les servían para nada. Ahora acaban de descubrir �vaya tragedia! que incluso la muy nueva teoría que ellos mismos han logrado crear, la relatividad especial de Einstein, en tanto que, a través de la fórmula (2), es la responsable de la "infinitésima contradicción" de los gemelos, tampoco les sirve para nada: les vale para nada porque para nada les vale. Mas... ¿nada vale?

Humana o divina, demasiado divina, ¿existe alguna ley eterna? Algunos historiadores sostienen que el gran Pitágoras ahogó al discípulo estúpido que se atrevió a demostrar la existencia de los números irracionales.

¿Cómo se puede ser un tan gran estúpido? Lo obscuro agrede lo lumínico. Es (im)propio del tonto con-fundir el arriba y el abajo. Todo fluye por el camino de lo paradójicamente coherente...

Los perros ladran, los gatos rebuznan, los asnos hablan y los tontos tontan. Una doble simpleza de lo presente empieza a resquebrajarse por ambas irracionales mitades. Ya no nos resta otra escapatoria que descontradecir la contradicción de los gemelos sin violar -por el breve momento este será el reto- la premisa de la constancia de la velocidad de la luz. Por todo lo comentado con anterioridad, parece que estamos atrapados en el interior de un laberinto aporético: refutar la irrefutable fórmula de la dilatación del tiempo relativista parece que conlleve, apodícticamente, refutar la irrefutable constancia de la velocidad lumínica, y versavice. �Nada que hacer! Pero luego ahí está, aporética, la contradicción de los dos gemelos.

Lo que está claro, aunque en estos precisos instantes a nuestra finita inteligencia le pueda aún parecer imposible, es que el incomprensible laberinto relativista tiene una salida. Ya que somos nosotros mismos quienes la creamos, estamos apodícticamente destinados a comprender nuestra propia representación del mundo. Si nuestra propia representación del mundo fuese contradictoria, no la comprenderíamos. Luego, aunque ahora aún no nos lo parezca, estamos destinados apodícticamente a crear la nueva teoría que nos permitirá escapar del incomprensible laberinto relativista...

El punto clave para encontrar la salida del aporético laberinto relativista, para escapar definitivamente de la "irrefutable" teoría de la relatividad, consiste en tener presente que si queremos construir una teoría que admita a priori la naturaleza absolutamente relativa del tiempo, entonces tal teoría también deberá admitir a priori la naturaleza absolutamente relacional del tiempo (nótese, ya que defiendo con insistencia la naturaleza relacional del tiempo, que en ningún momento estoy negando el genial descubrimiento de Einstein, a pesar de que no supo cómo resolverlo, de la relatividad del tiempo. Aún irracional pero en cósmica fusión, durante un breve eterno momento, el genio percibe cosas que ni tan siquiera él mismo alcanza a comprender). Luego, como pronto tendremos ocasión de comprobar, una métrica absoluta -no relacional- como la de Minkowski carece de sentido físico. Es una métrica plana "sólo para A". Tiene que ser sustituida por una métrica que sea capaz de trascender su propia película. Una métrica de naturaleza relacional �para A según B', �para C según A',... Muy así de tan simple, mas nunca nadie antes había reparado en ello.

Antes de introducir este nuevo tipo de métrica relacional, será conveniente sintetizar, en términos matemáticos, algunas de las ideas precedentes.

Sea �el diferencial de tiempo relacional para A según B, y sea �el diferencial de tiempo relacional para B según A. Supongamos que A está en reposo (siendo B el que se mueve) y que ambos tiempos están relacionados del siguiente modo:

(7)

Es decir, el tiempo para B según A transcurre �veces más rápido que el tiempo propio de A, es decir, el tiempo para A según A (todo observador tiene derecho, sin excepción posible, a considerarse a sí mismo como una referencia espaciotemporal "absoluta").

Pero para B, por la naturaleza relacional de las tetracoordenadas, el tiempo para A según B transcurre veces más rápido que su propio tiempo. Por tanto, a partir de (7) y por la naturaleza relacional del tiempo (5) se deduce, cosa que además es una absoluta trivialidad (dado que se considera que los relojes de A y B son idénticos, el tiempo propio es un invariante relacional: ):

(8)

También a partir de (7), pero ahora por la simetría según la velocidad del movimiento, (3), se deduce (pues ahora es B el que se considera en reposo):

(9)

Ambas fórmulas, (8) y (9), parten de un común origen, (7), y son trivial consecuencia directa de sendas evidencias: (5) y (3). Sin embargo, se repugnan entre sí.

La única salida satisfactoria, desde un punto de vista meramente matemático, es: . Cosa que, desde el punto de vista de la física, implica que la única solución lógica posible para la contradicción de los gemelos es:

(10)

Como ya sabíamos distintamente por la pura estructura lógica del lenguaje (me refiero al premeditado uso lógico del lenguaje a lo largo de todas las páginas precedentes), sin necesidad alguna de recurrir al lenguaje matemático, para ambos gemelos el tiempo ha transcurrido del mismo modo. Cualquier otra alternativa distinta, diga lo que diga la teoría de la relatividad, seríamos incapaces de entenderla. Ya lo advertí en mi Tractatus: nadie en este mundo entiende la teoría de la relatividad.

No es ningún problema no entender a Einstein. El verdadero problema es que algunos destacados intelectuales, tras tres siglos, aún no han conseguido entender a Newton (cosa que prueba que Newton es el mayor genio de la historia de la humanidad). Para Nietzsche, paradójico genio, un paradigma de genio es... Napoleón.

�Indignante! Los ignorantes, incapaces de salvarse a sí mismos, prefieren antes salvar el mundo (Nietzsche tiene toda la razón del mundo). Con tantos altruistas �cómo no vamos a ser optimistas!

Comprendo qué no comprendo. Jamás he aspirado a comprender �el' mundo. Entiendo qué entiendo. Siempre he aspirado a entender mi representación del mundo.

�Que la lógica llene la representación el mundo! No nos resta otra opción que construir una teoría alternativa a la relatividad especial. Una teoría que carezca de la contradicción de los gemelos. Lo haremos a lo largo de las próximas páginas...

��Ya lo sabía', dijo Einstein. (Advertencia sobre la verificación empírica)

Sir Arthur Eddington, que presumía de ser el único hombre en el mundo que comprendía la relatividad general de Einstein, organizó una expedición a no recuerdo dónde para observar un eclipse solar. Su misión consistía en verificar, durante el transcurso del eclipse, la conocida predicción de Einstein sobre el ángulo de desviación, a causa de la gravedad del sol, de los rayos lumínicos. A pesar de que, en aquel tiempo, los datos obtenidos por Eddington y sus colegas, datos muy imprecisos, parecían simpatizar mejor con la teoría de la gravedad de Newton (combinada con una teoría corpuscular de la luz) que con la teoría de la relatividad, la expedición resulto ser un éxito sin precedentes. Cumplió, claro está, con el objetivo previsto. Eddington certificó haber verificado la predicción de Einstein, que, a pesar del fraude, se convirtió en una de las predicciones más célebres de la historia de la ciencia.

Cuando a Einstein le comunicaron este tremendo éxito de Eddington respondió, sin ni siquiera dignarse a alzar la vista, con un lacónico �ya lo sabía'. A los relativistas les place interpretar esta respuesta, casi carente de entusiasmo a pesar de que parecía corroborar las teorías de Einstein, como una prueba de la fe del genio en el poder anticipatorio de la sola razón, de la ilimitada fe del genio en que, con el auxilio de la sola razón, se podría incluso llegar a comprender el mundo. ¿Tan ingenuo es un genio? ¿No sería más bien en el tan previsible triunfo de Sir sinvergüenza Eddington en lo que Einstein tenía depositada una inquebrantable fe? (La infalible fe de una nula confianza.) La vanidad y la estulticia nunca mienten.

Nunca faltará gente con la pericia necesaria para verificar lo que haga falta verificar. Por ejemplo, un reloj, incluso un tosco reloj de péndulo, siempre puede ser "ajustado" para que parezca corroborar lo que nos venga en gana corroborar. Pero ¿cuál es el extraño reloj que ha sido capaz de verificar empíricamente la contradicción de los gemelos? (Aunque ya hablaré con precisión de ello en otro lugar, anticipo ahora que toda teoría de la física -digna de ser tenida en consideración- está categóricamente obligada a definir lo que ella entiende por �reloj'. ¿Qué es un reloj según cada teoría histórica de la física? ¿Un fotón, que se caracteriza por su frecuencia, no es acaso un reloj? ¿Existe en la naturaleza algún extraño y antinómico reloj -aún aguardando en los remotos territorios metafísicos- capaz de "hacer ciertas" las contradictorias fórmulas de la teoría de la relatividad? Puesto que es manifiestamente cierto que el tiempo no se "detiene" a la velocidad de la luz -para un fotón el tiempo nunca se detiene-, no es necesario verificar nada para afirmar que la paradoja del fotón atemporal se resuelve así: la teoría de la relatividad es falsa.)

Otro ejemplo. El concepto �masa en reposo del fotón', ¿no es una evidente contradictio in adjecto? La proposición �la masa del ente E es igual a x kg' es ingenua. Pueril. Hay que complementarla sintéticamente del siguiente modo: �la masa del ente E es igual a x kg según la teoría T'. Teorías distintas "verán" masas distintas. Este hecho hay que tenerlo en cuenta a la hora de verificar empíricamente las masas correspondientes a los diversos entes, algunos ciertamente extraños, de la naturaleza. No hay que hacer demasiado caso a las verificaciones empíricas. �Incluso hay quienes creen que el sol no se mueve! Lo empírico es superfluo durante el proceso creativo de una nueva obra.

Es muy obvio que no sería lícito afirmar que, por regla general, todos los empíricos verifican con la mala fe. Simplemente les ocurre que no tienen otra alternativa que "filtrar" el mundo a través de nuestras limitadas teorías. Observamos el mundo a través de unas gafas con cristales azules, y, entonces, acabamos verificando que �en efecto! el mundo es azul. Pero sería imperdonable que sucumbiésemos ante el pueril engaño, pues, en el fondo, ya sabemos que lo que estamos viendo no es un mundo de color azul, sino el mundo, que es el que es, filtrado por el color azul.

Es muy obvio que hay que tener muchísima más fe, a pesar de sus claras limitaciones, en la sola razón que en los que sostienen que han verificado empíricamente que los círculos son cuadrados. El creador de lo nuevo tiene que precaverse ante todo posible artificio. Tiene que permanecer muy al tanto de todas las "verificaciones" que proliferan en la literatura científica oficial. Tales verificaciones siempre están adaptadas al color del cristal de las teorías consideradas oficialmente verdaderas (hoy en día están filtradas por el color negro oscuro: agujeros negros, materia oscura y energía oscura). Tales tramposos pozos saben cómo entorpecer el reconocimiento de la obra excelsa. Luego, aun inexorable, el destino retrocede.

LA MÉTRICA RELACIONAL

�Métrica relacional' es un concepto clave para la inteligencia plena del nuevo principio de inercia generalizado (principio éste que, digámoslo con claridad, más que una generalización supone una total refutación del principio de inercia clásico).

Antes se ha explicado que todas las tetracoordenadas, no sólo la temporal, tienen una naturaleza relacional. Una métrica no es otra cosa que una especie de regla que nos enseña cómo manipular las tetracoordenadas. Dado que éstas poseen una naturaleza relacional, así también la métrica.

Del mismo modo que no tiene el menor sentido hablar, en el contexto de una teoría que acepte que el tiempo no es absoluto, de �tiempo para A', tampoco tiene el menor sentido hablar de �métrica para A'. No existe la métrica para un único ente A. Sólo tiene sentido hablar relacionalmente de �métrica para B según A', de �métrica para A según B', de �métrica para C según A',...

Puesto que estamos suponiendo que todos los entes se mueven con movimiento relativo rectilíneo uniforme, lo único que podrá caracterizar la relación entre dos determinados entes será su velocidad relativa constante. Además, antes de que estemos preparados para elevarnos a un nivel lógico superior y alcanzar nuevas dimensiones énticas (la teoría conectada), la métrica aún deberá postularse para que sea acorde -aunque a los relativistas aún les pueda parecer que se repugnan entre sí- con estas dos condiciones: 1) para todos esos entes la velocidad de la luz en el vacío coincide con la constante , y 2) al menos para el caso concreto de los entes A y B que antes han sido analizados en la �contradicción de los gemelos', el tiempo tiene que transcurrir del mismo modo.

Al lector de las acertadas respuestas, poco debe importarle ya lo que los relativistas acérrimos aún puedan alegar. Tanto aquí en la tierra (por citar algún lugar) como en la luna o en cualquier otra parte, una contradicción es una contradicción. A es A, B es B y una contradicción es una contradicción. ¿Cómo aniquilar de una vez por todas la �paradoja de los gemelos'?

Hipótesis: la métrica relacional para B según A es (supongo que tanto A como B se mueven sobre la misma recta: el eje OX. La métrica es espacialmente cartesiana):

(11)

donde la constante �depende de una propiedad para B según A: su velocidad relativa constante (la constante que sigue no es igual a ninguna de las constantes que se han utilizado en expresiones previas):

(12)

Si ahora definimos el intervalo elemental al cuadrado para B según A como (nótese que, por la notación de Einstein, el intervalo contiene un sumatorio entre dos índices covariantes y dos índices contravariantes. Luego se trata de un escalar: es una magnitud invariante con respecto a todos los posibles entes):

(13)

donde:

(14)

Se define el diferencial de tiempo propio como �el diferencial de tiempo para A según A':

(15)

Por la invariancia del intervalo elemental al cuadrado:

(16)

Sustituyendo en (16), las expresiones (11) y (14) y teniendo en cuenta que �y que, por tanto, , y :

(17)

Por tanto:

(18 )

Y teniendo en cuenta (12):

(19)

(Nótese que si en lugar de la métrica (11) hubiésemos utilizado la métrica (1), en lugar de (19) habríamos vuelto a recaer en (2).)

Simétricamente, se pueden repetir los mismos cálculos �para A según B', y al final se obtiene:

(20)

Por tanto, la métrica relacional (11) permite eliminar la contradicción de los gemelos: el tiempo ha transcurrido igual para A que para B. Cuando se crucen en el mismo punto de la carretera ya no habrá entre ellos discrepancia temporal alguna. Ya no hay ninguna contradicción de los gemelos. (Nótese, de paso, que (20) también soluciona la paradoja del fotón atemporal.)

Además, puesto que la métrica (11) es proporcional a la de Minkowski, es fácil demostrar, igualando a cero el intervalo elemental al cuadrado, que tanto para A como para B la velocidad de la luz en el vacío coincide con la constante . Tanto para A como para B se cumple, pues, la premisa sobre la constancia de la velocidad lumínica. ¿Solucionada ya la aporía? ¿O aún está pasando una antinomia por aquí?

A pesar de que todo lo que hasta aquí se ha realizado ha sido con la sana intención de eliminar una contradicción, la contradicción de los gemelos, sin violar a su vez la premisa de la constancia de la velocidad de la luz, todo ello no ha supuesto más que un mero procedimiento ad hoc. Aunque plausibles, la métrica relacional (11) junto con la definición (12) han sido introducidas (casi) sin ningún tipo de justificación. Está claro, admitámoslo pues, que nada aún ha quedado formalmente demostrado hasta aquí.

Como es obvio la métrica relacional (11) no coincide con la de Minkowski, sino que es proporcional a ésta (curioso, ambas se aproximan cuando las velocidades de los entes son relativamente bajas). Este pequeño detalle implica que las transformaciones de Lorentz, matemáticamente consistentes con la métrica de Minkowski, han perdido cualquier sentido con la nueva concepción relacional de las tetracoordenadas. Por tanto, el siguiente paso lógico consistirá en hallar unas nuevas ecuaciones de transformación relacionales que sean consistentes con esta nueva forma de ver las distintas cosas, y que, por consiguiente, gracias a ellas, la hipótesis ad hoc (11) referente a la nueva métrica relacional se convierta en un postulado consistente, claro y distinto.

ECUACIONES DE TRANSFORMACIóN RELACIONALES

Las transformaciones de Galileo newtonianas no son válidas, pues son incompatibles con la constancia de la velocidad de la luz. Las transformaciones de Lorentz einstenianas no son válidas, pues son compatibles con la contradicción de los gemelos.

Las históricamente célebres trasformaciones de Lorentz entre A y B dicen que, dado un ente C que ocupa una cierta esfera temporal, el intervalo de tiempo registrado por A y el intervalo de tiempo registrado por B para ese ente C es relativo a la velocidad de B con respecto a A, , pero no hacen la menor mención a la velocidad del ente C con respecto a A, , o a la velocidad del ente C con respecto a B, ; el factor de Lorentz tan sólo depende de . No obstante, también es posible definir unas transformaciones de Lorentz entre A y C, y entonces, dado el ente B que ocupa una cierta esfera temporal, el intervalo de tiempo registrado por A y el intervalo de tiempo registrado por C para ese ente B resulta ser relativo a , pero no relativo a �ni a ; el factor de Lorentz tan sólo depende de . No obstante, rueda rueda, también es posible definir, del mismo modo rotativo anterior, unas transformaciones de Lorentz entre B y C, y entonces, dado... etc. Como es fácil comprobar, las transformaciones de Lorentz defienden un tipo de tiempo que es relativo a la velocidad (a través de ellas se deduce la fórmula (2)), pero discriminantemente relativo a la velocidad y de un modo selectivo: en cada caso anterior, dados los 3 entes, las transformaciones de Lorentz tan sólo hacen intervenir la velocidad relativa entre dos de estos entes, e ignoran las otras dos velocidades relativas. Las transformaciones de Lorentz no son "triangularmente simétricas".

Ignoran, en contra de lo que exige la naturaleza relacional del tiempo (5), que lo que deberían intentar resolver es un problema en cuya índole general intervienen 3 entes. En consecuencia, deberían intervenir también en ellas las 3 velocidades relativas entre estos 3 entes. Esto quiere decir que si a priori suponemos que el tiempo es relativo a la velocidad (cosa que, por el mero hecho de suponer que el tiempo es relativo, implica suponer a priori la naturaleza relacional del tiempo), entonces unas ecuaciones de transformación triangularmente simétricas deberán hacer intervenir a las 3 posibles velocidades citadas. No hay ninguna razón para que en cada uno de los 3 casos triangulares posibles se tome como privilegiada, aunque pueda ser reemplazada de un modo transferencial rotativo, una de las 3 velocidades en perjuicio de las otras dos. Las transformaciones de Lorentz "triseccionan" el tiempo relativo a la velocidad de Einstein.

Lo más suave que se puede oponer aquí, lo mínimo que se puede decir, es que las transformaciones de Lorentz ignoran la plena naturaleza relacional de cualquier tiempo que se pretenda a sí mismo como un tiempo de naturaleza absolutamente relativa. En este caso, ignoran la naturaleza relacional de un tiempo al que se lo supone relativo a la velocidad.

Además, en cuanto a lo que antes nos estaba ocupando, hay que insistir en que las transformaciones de Lorentz son "coherentes" con la contradicción de los gemelos. �Son coherentes con lo no coherente! Basta con esto para que queden refutadas.

.2 no es 33 no es 2.

Vagando de aquí para más allá y de allá para más aquí, con una falsa sensación de verdad, hemos tardado demasiado en descubrir el simétrico punto que parte hacia el camino acertado. Todo fluirá... hacia el lugar que le corresponde.

Estamos destinados a postular una nuevas ecuaciones de transformación relacionales, por supuesto, distintas de las de Lorentz, que deberán cumplir dos condiciones (la primera es una condición doble): 1) solucionar la contradicción de los gemelos a la vez que salvaguardan la premisa sobre la constancia de la velocidad de la luz, y 2) reducirse a las transformaciones de Galileo newtonianas en el caso particular en que las velocidades de los 3 entes sean bajas en comparación con la velocidad de la luz; esto es:

(21)

Seguidamente, a partir de la séptima línea desde aquí, introduciremos las funciones �y .

Estamos enfrentados a un problema general de 3 "entes": A y B, y C. Ensayemos, por todo lo que se acaba de comentar, las siguientes ecuaciones de transformación entre A y B para el ente C en coordenadas cartesianas diferenciales (la coordenada �x'):

Las transformaciones directas �para el ente C las escribiremos:

(22a)

(22b)

Las transformaciones inversas �para el ente C las escribiremos:

(23a)

(23b)

Para pasar de (22) a (23) se han permutado las "etiquetas" A y B y se ha tenido en cuenta la simetría según la velocidad del movimiento: .

(Para conocer exactamente (22) y (23), el lector impaciente puede consultar (42) y (43).)

Obviamente, si nuestro simple y único objetivo tan sólo fuese conseguir la constancia de la velocidad de la luz para todos los observadores con movimiento relativo rectilíneo uniforme, entonces nos bastaría con reinstaurar unas "nuevas" transformaciones de Lorentz "relacionales", y reinstaurar el ya desfasado factor de Lorentz:

(24)

Pues en este caso las ecuaciones de transformación (22) se reducirían a las transformaciones de Lorentz directas; y las ecuaciones (23) a las de Lorentz inversas (las transformaciones de Lorentz pueden consultarse en cualquier libro de texto sobre relatividad especial).

Pero no estamos luchando por un simple objetivo. Tampoco por un objetivo simple. Estamos porfiando, con la meritoria intención de escapar del aporético laberinto relativista, por un doble objetivo: además de la constancia de la velocidad de la luz para los observadores con movimiento relativo rectilíneo uniforme, queremos solucionar, cosa que las transformaciones de Lorentz son incapaces de conseguir, la aporética contradicción de los gemelos. Luego la expresión (24), que lamentablemente nos reconduciría de nuevo hacia las transformaciones de Lorentz, no nos vale.

Ya que no nos vale, la única alternativa lógica a (24) es, necesariamente:

(25)

Aún ignoramos qué son �y �por separado, pero al menos podemos asegurar -a no ser que pretendamos recaer en la contradicción de los gemelos- que . Paso a paso, nudos y entuertos se deshacen.

Por (22a) y (23a):

(26)

De donde se deduce:

(27)

ECUACIONES DE TRANSFORMACIóN RELACIONALES TENSORIALES

Las ecuaciones de transformación �para el ente C, (22), pueden ser escritas en notación tensorial como:

(28)

Consultando (F-3), ver el formulario, vemos que pueden ser escritas de forma más compacta del siguiente modo (la identificación de cada parte de (28) con la expresión que sigue es evidente):

(29)

Análogamente, la transformación inversa �para el ente C, (23), se escribe:

(30)

La cual, en atención a (F-4), puede compactarse como:

(31)

Por tratarse de transformaciones inversas entre sí:

(32)

donde �es el tensor identidad.

Es fácil comprobar que:

(33)

Comparando (33) con (32) se deduce:

(34)

Y sustituyendo (27) se obtiene una expresión que relaciona las velocidades relativas entre los tres entes:

(35a)

De esta expresión se puede despejar, por ejemplo, la velocidad . Después de unas operaciones elementales, se obtiene la regla que nos enseña cómo "sumar" velocidades:

(36)

Por la simetría de la transferencia triangular, a partir de (35a) se deducen, rueda rueda, las expresiones:

(35b)

y:

(35c)

(Recordemos que hemos supuesto que los 3 entes se mueven a lo largo del eje OX, por tanto todas las velocidades que aparecen en esas fórmulas anteriores se refieren a las componentes X.)

DETERMINACIóN DE �y

Para deducir todo lo precedente nos ha bastado con saber que las funciones indeterminadas �y �no son idénticas, ver (25), y que cumplen la condición (27). Pero aún ignoramos la expresión exacta que corresponde a cada una por separado.

Las determinaremos de tal modo que la contradicción de los gemelos quede aniquilada. Como antes vimos, tanto para A como para B tiene que haber transcurrido exactamente el mismo tiempo desde que empezaron su pequeño viaje hasta que se cruzaron en el mismo punto de la carretera entre Girona y Barcelona. Con más precisión: el tiempo para A según B tiene que coincidir con el tiempo para A según A: .

Si hacemos "C=A" (la simbología de la izquierda es éntica, no hace referencia a ninguna de las anteriores funciones) en la ecuación de transformación relacional (22a), ésta queda reducida a dos entes, y se obtiene:

(37)

de donde se deduce (puesto que cualquier ente tiene derecho a considerarse a sí mismo en reposo, la variación diferencial de la coordenada espacial para A según A es nula: ):

(38)

Además, sustituyendo (38) en (27), si "C=A":

(39)

Para eliminar la contradicción de los gemelos también se tendrá que cumplir: . De un modo completamente análogo a estos últimos razonamientos, si ahora hacemos "C=B" en la ecuación de transformación relacional inversa (23a) y volvemos a tener en cuenta (27) se obtienen, simétricamente, los siguientes resultados:

(40)

y:

(41)

La única respectiva y simultánea manera de obtener (38) y (39) cuando "C=A" y (40) y (41) cuando "C=B" es:

(42)

y:

(43)

Nótese que siempre se verifica (27).

Para escribir las nuevas ecuaciones de transformación relacionales directas basta sustituir (42) en las dos ecuaciones (22). Para las inversas, se habrá de sustituir (43) en (23).

Estas nuevas ecuaciones de transformación relacionales, que, en acuerdo con (21), se reducen a las transformaciones de Galileo newtonianas cuando las velocidades de los entes son pequeñas comparadas con la velocidad de la luz, reclaman su derecho histórico para reemplazar a las de Lorentz.

Pero aún no hemos demostrado su consistencia...

TRANSFORMACIóN DE LA MÉTRICA RELACIONAL

Aunque se había introducido mediante un mero procedimiento ad hoc, antes habíamos visto que una métrica de tipo relacional como la de la hipótesis (11) lograba el meritorio doble objetivo que antes nos habíamos exigido: 1) la constancia de la velocidad de la luz para todos los entes con movimiento relativo rectilíneo uniforme, y 2) aniquilaba la contradicción de los gemelos. Pero faltaba aún encontrar unas ecuaciones de transformación relacionales, asociadas a esta nueva métrica, que demostraran su consistencia.

Elevemos la hipótesis (11) a la categoría de postulado. Vamos a demostrar que este postulado es, en efecto, plenamente consistente con las transformaciones relacionales (22) y (23) .

Postulado: sea la métrica relacional para C según A:

(44)

con:

(45)

¿Cuál será la métrica relacional para C según B? ¿El lector ya sabe la respuesta? Bien. La respuesta acertada es fácil, pero aún hay que demostrarla. Las transformaciones relacionales (22 ) y (23) serán las encargadas de hacerlo.

Consultando (F-6) en el formulario:

El tensor �es el mismo que actúa en (30) o (31). Por tanto:

(46)

Recordando las fórmulas (43) y (45) se obtiene:

(47)

A partir de (47) y teniendo en cuenta (35) y (43) y que, por la simetría según la velocidad del movimiento:

, �y (48)

se puede escribir:

(49)

Finalmente:

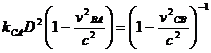(50)

Por tanto, sustituyendo (50) en (46), la métrica relacional para C según B resulta ser:

(51)

con:

(52)

Quedando así demostrada la consistencia del postulado (44) a través del cual se definió la nueva métrica relacional (basta que el lector compare (44) y (45) con (51) y (52)).

La nueva métrica relacional (44) es proporcional a la métrica de Minkowski. Desde un punto de vista matemático, la novedad es nimia. Sin embargo, esta nimia novedad matemática nos está obligando a revisar en profundidad todos los conceptos y todas las proposiciones de la física actual.

También es conveniente seguir insistiendo en que la presente teoría relacional, aunque esté libre de las contradicciones de la relatividad especial, no puede ser considerada más que un sencillo caso especial de una nueva teoría general: la teoría conectada.

A la hora de generalizar la presente teoría relacional (para adaptarla al fenómeno gravitatorio y al nuevo principio de inercia tetradimensional) habremos de tener en cuenta que no es la métrica local, la métrica en el punto en el que el mismo observador se encuentra, la que deberá reducirse a la métrica de Minkowski (suponiendo que no existan aceleraciones relativas entre C y A, la métrica local �para C según A' es relacionalmente proporcional a la de Minkowski), sino la métrica propia �para A según A'.

MÉTRICA RELACIONAL TETRADIMENSIONAL (4-D)

El presente capítulo, aparte de algunas novedades, generalizará los resultados ya obtenidos anteriormente. Hasta ahora hemos supuesto que los 3 entes A, B y C se movían a lo largo del eje OX. Por esto nos ha bastado trabajar con 2 dimensiones tensoriales. Hay que ampliar los resultados anteriores a las 4 dimensiones espaciotemporales (las 3 dimensiones espaciales continuarán siendo tratadas en coordenadas cartesianas).

Puesto que disponemos de libertad para etiquetar una dirección, supondremos que los entes A y B siempre se mueven a lo largo de la dirección del eje OX, entre tanto que el tercer ente C es libre de moverse en cualquier otra posible dirección (por supuesto, los movimientos relativos entre los 3 entes continúan siendo rectilíneos uniformes).

Postulado: La métrica relacional tetradimensional para C según A es:

(53)

con:

(54)

Obsérvese que cuando la velocidad para C según A, es decir, la velocidad relativa de C con respecto a A, es relativamente baja comparada con la velocidad de la luz, , la métrica relacional (53) coincide aproximadamente con la métrica relativista absoluta de Minkowski. Lo cual significa que, desde el punto de vista de la nueva teoría relacional, la relatividad especial sólo puede proporcionar resultados numéricos aceptables cuando las velocidades de todos los entes son pequeñas comparadas con la velocidad de la luz. Curiosa conclusión: la nueva teoría relacional inflige a la relatividad especial la misma suerte que esta última creyó haber infligido a las teorías newtonianas.

De (53) y (54) se deduce que tan sólo la métrica relacional propia, definida como:

(55)

coincide exactamente con la métrica plana de Minkowski (1).

Otra propiedad de la nueva métrica (53), también muy fácil de comprobar, es su simetría relacional con respecto de los dos entes, es decir:

(56)

Esta simetría es consecuencia de la simetría del movimiento (3).

La métrica relacional también es simétrica, por supuesto, con respecto a los dos subíndices tensoriales covariantes (que en la presente notación se han dado por sobreentendidos).

EL INTERVALO DIFERENCIAL ELEMENTAL AL CUADRADO

El intervalo diferencial elemental al cuadrado para C según A se define relacionalmente como:

(57)

donde:

(58)

y:

(59)

Los índices tensoriales nos indican que la expresión (57) es un escalar invariante (se sobreentiende la notación de Einstein). El significado semiótico de los "subíndices" énticos es el mismo de siempre: �(...) para C según A'.

Por ser la expresión (57) un escalar invariante, resultará ser la misma para todos los entes posibles. Así, dado un ente cualquiera C, la expresión (57) para C según A será la misma que la expresión para C según B, siendo también A y B entes cualesquiera (recordemos que en la presente teoría relacional siempre estamos suponiendo que los movimientos relativos entre todos los entes son rectilíneos y uniformes):

(60)

El diferencial de tiempo propio se define como el diferencial de tiempo para un ente A según A:

(61)

En este caso particular, "C=A", la métrica relacional para C según A se reduce a la métrica relacional propia (55), y, por la definición (60), se obtiene (nótese que ):

(62)

Por la expresión (60) sabemos que (62) es un escalar invariante. Luego el tiempo propio también es un escalar invariante ("" es una mera constante).

Por todo ello, la expresión (57) puede ser desarrollada como:

(63)

Como ya vimos en (12), (18) y (19), la expresión definida en (54) es la que permite eliminar la contradicción de los gemelos.

El intervalo diferencial elemental al cuadrado para C según A cuando el ente C es un fotón (luz) cumple que:

(64)

y por (63) (nótese que la constante relacional entre el fotón C y el ente A, , se simplifica):

(65)

Es decir, la velocidad de un fotón coincide con la constante "".

Para deducir (65) ha sido imprescindible hacer uso de (64). Puesto que (64) es un escalar invariante, se obtiene que: para todos los entes en movimiento relativo rectilíneo uniforme la velocidad de la luz siempre coincide con la constante "".

Por otro lado, nótese que en general se tiene que cumplir que: . Cosa que según (63) implica que:

(66)

Reagrupando términos se obtiene, después de simplificar la constante relacional :

(67)

Es decir, la velocidad relativa entre dos entes cualesquiera C y A no puede superar la constante "", que se convierte, de este particular modo, en la velocidad máxima posible entre dos entes cualesquiera.

Los resultados (65) y (67) de la nueva teoría relacional coinciden con las famosas premisas o conclusiones de la teoría de 1905 de Einstein: la relatividad especial. Pero ¿son ciertos estos resultados? Expresado con más precisión: ¿son resultados generales?

La respuesta es un categórico no. Para obtener estos resultados se ha utilizado la métrica relacional postulada en (53), la cual tan sólo es válida cuando el movimiento relativo entre los entes A y C es rectilíneo uniforme. Es decir, no es válida cuando intervienen aceleraciones relativas o cuando intervienen campos gravitatorios. La métrica (53) a partir de la que se han deducido los famosos resultados (65) y (67) es tan sólo una métrica de aplicación particular. Por tanto, los resultados que a través de ella se puedan obtener nunca deben ser considerados como unos resultados con carácter general.

Para determinar las métricas cuando intervienen aceleraciones relativas y/o campos gravitatorios hay que hacer uso de las ecuaciones generalizadas (171) y (172) de la teoría conectada (La métrica (53) tan sólo representa la solución trivial de éstas ecuaciones. Ver Tractatus physico-philosophicus). Al ser todas estas métricas generalizaciones de (53), es decir, en general distintas a (53), no tienen por qué predecir que la velocidad real de la luz para todos los observadores viene determinada por la misma constante "". Tampoco tienen por qué estar obligadas a afirmar que el valor numérico de la constante "" -que, en efecto, es una constante- representa la máxima velocidad posible de la naturaleza.

La velocidad real de la luz se obtiene igualando a cero el intervalo elemental al cuadrado. Es una completa obviedad que la velocidad así obtenida, si la métrica no viene dada por (53), podrá ser mayor o menor que la representada por la famosa constante "". Por tanto, lo máximo que podemos decir al respecto es que la constante "" tan sólo representa la velocidad local de la luz en el vacío. La velocidad no local, incluso suponiendo una total ausencia de gravedad y dependiendo del caso particular que se considere, podrá ser mayor o menor que "" (pero, supuestas unas mismas condiciones para un fotón y para cualquier otro ente, éste nunca podrá superar la velocidad real del fotón).

La existencia de una velocidad máxima de la naturaleza es incompatible con la premisa de todas las premisas: la invariancia de las leyes físicas (la absoluta relatividad del movimiento)

El "espacio absoluto" para un número finito de cuerpos sería "algo" que permanece en absoluto reposo, o en movimiento rectilíneo uniforme, con respecto al centro de masas de tales cuerpos. El espacio absoluto de Newton, el sensorio de Dios, sería algo que permanece en absoluto reposo, o en movimiento rectilíneo uniforme, con respecto a �el' centro del Universo, luego no existe. No existe ningún metafísico referencial absoluto -o inercial- con el que describir el movimiento de los cuerpos. La premisa de todas las premisas, para mí tan clara y distinta como para Descartes pudiese serlo su célebre cogito, es: �el movimiento es absolutamente relativo'. Todo cuerpo, sin excepción alguna posible, tiene el pleno derecho a autoconsiderarse en reposo, e interpretar, consecuentemente, que son los restantes cuerpos del universo los que se mueven con relación a él. Negar dicha premisa equivaldría a negar la invariancia universal de las leyes físicas y a creer que aún existen referenciales privilegiados -¿cuáles?- con relación a los demás. Negar la absoluta relatividad del movimiento equivaldría a afirmar la existencia de referencias absolutas: el espacio absoluto de Newton, en definitiva.

En particular, nuestra propia tierra tiene pleno derecho a considerarse a sí misma en reposo. No hace falta viajar a lejanas galaxias ni observar lo que ocurre en los modernos aceleradores de partículas (al fin y al cabo, en tales máquinas, los sabelotodo verificarán lo que les venga en gana verificar. Me atrevo a predecir que hasta serán capaces de ver, a mayor gloria, �el mismísimo origen divino de �el' tiempo!) para alcanzar valiosas "iluminaciones". Desde nuestra propia tierra se observan estrellas pertenecientes a nuestra propia galaxia que describen una vuelta completa a nuestro alrededor en tan sólo 24 horas. Sabiendo que la longitud de una circunferencia es y que la distancia del sol a la tierra es de unos 150 millones de kilómetros, propongo al lector un muy sencillo cálculo: ¿cuáles son las velocidades de las estrellas cuyas distancias con respecto a la tierra son mayores en tan sólo unas 28 veces la distancia tierra-sol? ¿Superan estas velocidades el valor de c=300000km/s? ¿Son "aparentes" los eternos movimientos de tales estrellas? ¿Tanto nos engañan los sentidos? ¿Tanto nos engaña la razón? ¿Es un malin génie el malin génie de Descartes? ¿Acaso hemos de regresar a las dicotomías newtonianas �movimiento verdadero-movimiento aparente' y �sistema inercial-sistema no-inercial'? ¿No es el movimiento verdadero y real de tales estrellas, precisamente, la clara evidencia de que los cuerpos libres son libres de no moverse según el capricho del principio de inercia clásico? ¿No resulta obvio que es necesario un nuevo principio de inercia generalizado, un principio que no obligue a que el movimiento de los cuerpos libres tenga que ser, necesariamente, rectilíneo uniforme? ¿Acaso a un cuerpo (tetradimensionalmente) libre no le está permitido, incluso, estar acelerado?

¿Qué es lo que aún todavía sostiene la doctrina relativista? ¿No es acaso la existencia real de sistemas inerciales y no-inerciales lo que aún postula el absurdo y dicotómico principio de equivalencia de Einstein? ¿Por qué es la tierra la que verdaderamente gira sobre sí misma? ¿Por qué los relativistas aún sostienen que la tierra es un sistema no-inercial provisto de un movimiento de rotación absoluto? El espacio absoluto ya no existe �nunca ha existido! luego ¿rotación absoluta con respecto a qué?

El relativismo, que empezó con buen pie en 1905 refutando el espacio absoluto de Newton, ha regresado de nuevo, "gracias" al principio de Equivalencia de Einstein, al espacio absoluto y a la dicotomía inercial-no inercial newtonianos. Cosa que, a pesar de ser contradictoria y muy absurda, tiene su interesada "lógica": si realmente existen velocidades superiores a "c", entonces la teoría de la relatividad, tanto la especial como la general, queda refutada incontinenti. ¿La pura evidencia no nos obliga a concluir que las velocidades reales de la naturaleza pueden superar con creces el valor de "c"? ¿Ha terminado ya el lector ese muy sencillo cálculo? ¿No estará su espíritu infernalmente poseído por algún oscuro genio maligno? Espero que el lector haya sabido acertar todas las respuestas.

La pura evidencia es eterna; el sesudo prejuicio, efímero (el principio de inercia clásico, por ejemplo).

Otra clara limitación de la teoría relacional que aquí se está exponiendo, es que sólo es capaz de discernir a los entes entre sí según su velocidad relativa. Expresado de un modo más preciso: si la velocidad relativa entre dos entes A y B es nula, entonces tales entes juegan, con respecto a las ecuaciones de transformación relacionales, un idéntico papel. Son, para dichas ecuaciones, énticamente indiscernibles:

Si �entonces "A=B" (68)

Sabemos, no obstante, que el tiempo es relativo a la posición en el medio gravitatorio. Sabemos que si los entes A y B son sendos relojes idénticos situados en diferentes puntos del medio gravitatorio, entonces, aunque la velocidad entre ellos sea nula, el tiempo no discurrirá del mismo modo para ambos. Luego, el formalismo de una teoría general (la teoría conectada) debe ser capaz de discriminar entre una gama de alternativas mucho más amplia. Debe admitir, incluso suponiendo que la prótasis de la anterior implicación (68) sea la misma, la posibilidad de que A sea discernible de B.

 

ECUACIONES DE TRANSFORMACIóN RELACIONALES 4-D

Las presentaremos sin previa justificación. Directamente. Más adelante el lector ya tendrá ocasión de demostrar la consistencia entre las nuevas ecuaciones de transformación relacionales y la nueva métrica relacional (53).

Transformación directa de �para el ente C:

(69a)

(69b)

(69c)

(69d)

Estas son las 4 transformaciones directas. Las expresiones �y �se escriben como:

(70)

y:

(71)

Si tenemos en cuenta las relaciones (35), esta última expresión también puede ser escrita como:

(72)

En efecto, sustituyendo (35b) y (35c) en la expresión anterior:

(73)

y por (35a):

(74)

Transformación inversa de �para el ente C:

(75a)

(75b)

(75c)

(75d)

Estas son las 4 transformaciones directas. Las expresiones �y �se escriben como:

(76)

y:

(77)

Si tenemos en cuenta las relaciones (35), esta última expresión también puede ser escrita, en perfecta simetría con respecto a la (72), como:

(78)

Como ya ocurría en (34):

(79)

y por (72) y (78):

�(80)

Ha tenido que pasar más de un siglo para que la contradictoria relatividad especial quede refutada. La nueva teoría relacional está destinada a ocupar su lugar. A los contrariados relativistas, que durante tantísimo tiempo han sido incapaces de detectar ni una sola contradicción en una teoría tan "perfecta" como la contradictoria relatividad especial, tal vez, paradójicamente, les dé por preguntar ahora: ¿no habrá alguna contradicción en la nueva teoría relacional? Tan serenísima duda conlleva un espléndido augurio: aunque un poco demasiado tarde, tal vez los inteligentísimos relativistas estén ya empezando a descontradecirse.

Es obvio que a todos aquellos que se han familiarizado, durante demasiado tiempo, con las transformaciones de Lorentz einstenianas, al principio les resultarán increíbles y sorprendentes las nuevas ecuaciones de transformación relacionales. Y, en efecto, son sorprendentes e increíbles. Sería muy conveniente que el lector inteligente empiece ya a adiestrarse en su empleo. Vamos a comentar aquí las ecuaciones (69c), (69d), (75c) y (75d).

Es importante que nunca se olvide que las nuevas ecuaciones de transformación relacionales tratan a las tetracoordenadas relacionalmente y que, dichas ecuaciones no hacen referencia a tan sólo 2 entes, sino a 3: A y B, y C. Para empezar, supongamos el caso especial en el que el tercer ente C esté en reposo con respecto a A. Entonces, como vimos en la proposición (68), el ente A y el ente C son énticamente indiscernibles para las ecuaciones de transformación relacionales. Por tanto, "A=C" y, trivialmente, las componentes de la velocidad relativa de C con respecto a A serán:

, �y (81)

y con respecto a B:

, �y (82)

De las respectivas dos últimas expresiones de (81) y (82) se obtiene:

(83)

Por tanto, con total independencia de cuales puedan ser los valores de �y de , las ecuaciones (69c), (69d), (75c) y (75d) se verifican trivialmente.

Pero, en general, el tercer ente C no tiene por qué coincidir ni con A ni con B. Además puede moverse no sólo en la dirección OX, sino en cualquier otra posible dirección. En este caso general tenemos dos alternativas:

1) Si , entonces, por (72) o (78), (84)

2) Si , entonces (85)

En el primer caso, también trivial, no se viola ni la naturaleza relacional de las tetracoordenadas ni la simetría según la velocidad del movimiento relativo rectilíneo uniforme.

En el segundo caso, las "distancias diferenciales transversales" (la "y" o la "z") para el ente C no son las mismas según A que según B, cosa completamente lógica si tenemos en cuenta que hemos partido del supuesto de que la componente "x" de la velocidad para el ente C tampoco era la misma según A que según B. Luego tampoco se viola aquí la simetría según la velocidad (3). Además (80) garantiza la naturaleza relacional de las coordenadas transversales.

En definitiva, las nuevas ecuaciones de transformación relacionales (69) y (75) han conseguido eliminar la paradoja de los gemelos a la vez que respetan la naturaleza relacional de las tetracoordenadas y la simetría (3) del movimiento. Por otro lado, como vimos en (65), también respetan la premisa de la constancia de la velocidad de la luz para todos los entes cuyo movimiento relativo sea rectilíneo uniforme.

Pero aún falta demostrar que la nueva métrica relacional (53) es consistente con las nuevas transformaciones relacionales.

ECUACIONES DE TRANSFORMACIóN TENSORIALES 4-D

Transformación directa �para el ente C (ver (69)):

(86)

Transformación inversa �para el ente C (ver (75)):

(87)

Aparte de (69) y (75), se han tenido en cuenta (F-3) y (F-4).

Es fácil demostrar que:

CONSISTENCIA DE LA MÉTRICA RELACIONAL Y LAS TRANSFORMACIONES RELACIONALES

Sea:

(88)

con:

(89)

Entonces, por (F-6):

Tras unas operaciones elementales:

(90)

Al igual que vimos en (50):

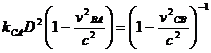(91)

y por (89) y (78):

(92)

Por tanto, sustituyendo (91 y (92) en (90), se obtiene:

(93)

con:

(94)

Queda aquí demostrada la consistencia entre la métrica relacional y las ecuaciones de transformación relacionales. Hemos cumplido, es nuestra libre obligación ética, con los objetivos que antes se habían anunciado.

El inteligentísimo es al sesudo prejuicio lo que el genio es a la pura evidencia. (In)visible obscuridad, luz (in)visible

La historia demuestra que... con excesiva frecuencia, la inteligencia excesiva es enemiga de la genialidad pura. Son ya muchos los personajes eminentes, algunos muy (re)conocidos, los que han recibido mis nuevas teorías. Salvo alguna prometedora excepción, que me ha confesado que aún todavía no ha detectado ningún error en ellas, la inmensa mayoría de esos personajes está optando por guardar silencio. ¿Ignaro silencio? Aun inexorable ¿el destino retrocede? Tranquilos. La eternidad nunca tiene prisa. Tarde o menos tarde, tal vez antes de un siglo, cualquier teoría -oídlo bien, cualquier teoría- se descubre errónea. Pero por mucho que algunos prefiráis continuar jugando a ser una cierta excesiva especie de genios despistados, por mucho que al interés no le interese lo desinteresado, al menos ahora ya sabéis lo que antes no sabíais: que vuestras tan excelsas transformaciones de Lorentz ya no son las únicas que consiguen salvaguardar vuestra tan intocable premisa: la de la constancia de la velocidad de la luz a través de la nada. Premisa que, por si aún todavía no os ha quedado claro, se ha convertido en un dogma absurdo: es incompatible con la absoluta relatividad del movimiento y, por ende, con la invariancia universal de las leyes físicas. La teoría conectada, que es la legítima generalización lógica de la teoría relacional que aquí se ha presentado, ya lo ha logrado superar. El relativismo ha muerto.

Los positivistas científicos, los mismos que tan sólo creen en las evidencias empíricas y que -en consecuencia- saben fehacientemente cuándo comenzó �el' mundo, sostienen que no existen (que no tienen justificación empírica alguna) los metafísicos juicios sintéticos a priori de Kant (por cierto, os iría bien leerlo y entenderlo). Pero el juicio �la constante "c" representa la máxima velocidad posible de la naturaleza', ¿acaso no sería para el relativismo un juicio sintético a priori? ¿Cómo sino a posteriori?

No añadiré más comentarios. El caro lector de las acertadas respuestas, tal vez el mismo anónimo lector que en otro filosófico lugar ya me ayudó a demostrar, por el mero hecho de leer el Tractatus, la invariancia universal de las leyes físicas, no los necesita.

TRANSFORMACIóN RELACIONAL DE VELOCIDADES

Tanto a partir de (69) como de (75) es posible deducir las ecuaciones de transformación para las velocidades.

Combinando (69a) con (69b) se obtiene:

(95)

Por tanto:

(96)

Que es la misma fórmula que había sido obtenida en (36) (el significado de las variables que en ella intervienen es obvio).

La transformación de las componentes transversales se obtiene de forma parecida. Basta tener en cuenta (69a) y (69c) o (69d). Resultan:

(97)

y:

(98)

Como era previsible, las expresiones matemáticas para la transformación relacional de velocidades coinciden con las de la relatividad especial.

Las transformaciones inversas de velocidad se pueden obtener de las 3 anteriores simplemente haciendo el cambio: .

REESCRIBIENDO LAS TRANSFORMACIONES RELACIONALES

Sacando factor común �en el segundo miembro de la ecuación (69a), ésta se puede reescribir como.......

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

�no implica que . Falta una constante de integración. "Multiplicando por dos" el argumento, �y �no implican que si �entonces tenga que ser también . Pues, en general, será . Es decir, dos sucesos C y D pueden ser simultáneos para A, pero no serlo para B (salvo casos particulares, dos sucesos que sean simultáneos para A no lo serán para B, y vicecersa). Pero de la no simultaneidad general de los sucesos, no es lícito concluir, como argumentan los textos relativistas, que el tiempo es relativo, entendiendo �relativo' como un concepto opuesto al �absoluto' newtoniano. Lo máximo que es lícito deducir sobre ello es que la velocidad de propagación de la luz es finita y que, por tanto, los tiempos de retardo respectivos que tarda la luz en alcanzar a A y a B para informarles de los sucesos C o D son tiempos finitos y, en general, distintos. (Lo que en relatividad otorgaba una naturaleza relativa y genuinamente no newtoniana al tiempo era el factor de Lorentz -éste era el culpable de hacer envejecer a ritmos distintos a distintos observadores-, no la no simultaneidad general de todos los sucesos.)

(Continuará)

FORMULARIO

Vectores base A:

Vectores base B:

Transformación �de los vectores de la base:

(F-1)

Transformación �de las componentes de un vector:

(F-2)

Expresión (F-2) en notación matricial relacional:

(F-3)

Transformación inversa de (F-3), , en notación matricial relacional:

(F-4)

Transformación �de la métrica:

(F-5)

Expresión (F-5) en notación matricial relacional:

(F-6)

Transformación inversa de (F-6), , en notación matricial:

(F-7)

PARA REFLEXIONAR

La invariancia universal de las leyes físicas -la igualdad, la ausencia de privilegios, de todos los referenciales de la naturaleza- implica la absoluta relatividad del movimiento, pues si ésta fuera falsa, entonces existirían referenciales privilegiados.

El lector deberá tener siempre en la mente la invariancia universal de las leyes físicas: El espacio absoluto no existe: No existen observadores privilegiados. Cosa que implica que todos sus razonamientos y todas sus reflexiones, por mucho que violenten las prejuiciosas ideas, deberán supeditarse a la premisa de todas las premisas: �El movimiento es absolutamente relativo.

LA PARADOJA CINÉTICA

Imaginemos un "universo" en el que tan sólo existen dos cuerpos, y que ambos son astros habitados por seres inteligentes. A habita en el cuerpo A, de masa M, y B en el cuerpo B, de masa m. Supongamos que la masa de B es despreciable comparada con la de A. Es decir, la masa de B es mucho más pequeña que la de A: . Supongamos, además, que entre ambos cuerpos no existe ningún tipo de interacción y que, además, su movimiento relativo es rectilíneo uniforme, siendo su velocidad relativa lineal ,, muy pequeña comparada con la constante "" .

Recordando que el espacio absoluto y las referencias inerciales absolutas no existen y que, en este "universo", tan sólo existen A y B y nada más, ¿cuál será la energía total de este universo?

Tanto A como B trabajan con la fórmula (2). Trabajan con la teoría de la relatividad (considerando que las velocidades son bajas).

Desde el punto de vista de A, él tiene pleno derecho a considerarse en reposo siendo B el que se mueve con respecto a él. Por tanto, calcula la siguiente energía (no tendremos en cuenta lo que en relatividad se denomina energía en reposo):

Pero B considera, también con pleno derecho, que es él el que permanece en reposo y A el que se está moviendo. Por tanto, calcula la energía siguiente:

Supongamos que se quiere emplear esta energía para proporcionar luz eléctrica a los habitantes de los cuerpos A y B (estamos tratando con conceptos y proposiciones. El problema técnico sobre cómo transformar energía cinética en energía eléctrica no nos interesa aquí). ¿Durante cuánto tiempo dispondrán de luz estos habitantes? La masa de A es mucho mayor que la de B y, por tanto: . Por tanto, desde el punto de vista de B tales habitantes dispondrán de luz durante mucho más tiempo que desde el punto de vista de A. Según B, por decir algo, durante 100 años. Pero, según A, por decir algo consistente con lo anterior, apenas dispondrán de energía eléctrica durante unas pocas horas (el desacuerdo exacto en la duración de la energía eléctrica dependerá, claro está, de la diferencia entre las masas de A y B).

¿Cuál de los dos puntos de vista es el verdadero? ¿Acaso A no tiene derecho a considerarse en reposo? ¿O es B el que no lo tiene?

¿Acaso la teoría de la relatividad contradice la simetría según la velocidad del movimiento rectilíneo uniforme ? ¿Hay que volver al espacio absoluto -entendido como "el" sistema de referencia inercial absoluto- de Newton?

LA DICOTOMíA FUERZAS A DISTANCIA-FUERZAS DE CONTACTO

Históricamente, una "fuerza a distancia" es la que la tierra ejerce sobre una piedra, haciéndola caer, o la que las cargas eléctricas de un peine ejercen sobre nuestros cabellos; y una "fuerza de contacto", la que una cuerda atada a un cuerpo ejerce cuando tira de él.

A las fuerzas a distancia se les asocian energías potenciales. De tal modo que una piedra que cae, a causa de la fuerza a distancia ejercida por la tierra sobre ella, conserva su energía. El aumento de su energía cinética (a causa del aumento de su velocidad) durante su caída está compensado exactamente por la disminución de su energía potencial asociada (a más proximidad con el suelo, menos energía potencial). La piedra "en sí" mantiene constante su energía (conservación de la energía mecánica).

En cambio, a las fuerzas de contacto no se les asocian energías potenciales. De tal modo que un cuerpo que aumenta su velocidad, a causa de la fuerza de contacto ejercida por una cuerda sobre él, no conserva su energía. El aumento de su energía cinética mientras la cuerda tira de él no está compensado por energía potencial alguna. Obviamente se considera que la energía total se conserva, pues este incremento de energía cinética proviene del trabajo realizado por la cuerda que tira del cuerpo (teorema de las fuerzas vivas). Pero, el cuerpo "en sí", no mantiene constante su energía.

Pero ¿no son las fuerzas a distancia tan de contacto como las fuerzas de contacto? ¿No son las fuerzas de contacto tan a distancia como las fuerzas a distancia? ¿No es la fuerza de contacto ejercida por la cuerda sobre el cuerpo una fuerza a distancia (la suma de una infinidad de microscópicas fuerzas a distancia entre las partículas del cuerpo y las de la cuerda)? ¿No es factible considerar que, al igual que la piedra, el cuerpo está "cayendo" en el "campo" generado por el conjunto de tales fuerzas? ¿Por qué no interpretar que el cuerpo "en sí", del mismo modo que antes la piedra "en sí", también conserva su energía? El trabajo realizado por la cuerda, ¿no ha sido acaso invertido en generar dicho campo con su correspondiente energía potencial asociada?

No sé lo que les parecerá a los demás, pero a mí �me sugiere �movimiento absolutamente relativo'.

ALGO SE MUEVE...

Un movimiento sólo puede ser uniforme con respecto a otro movimiento, como, por ejemplo, el de las manecillas de un reloj. Un movimiento que sea uniforme con respecto a determinado reloj, ya no será uniforme con respecto a otro reloj idéntico pero que marque un "tiempo acelerado" con respecto de aquél (porque este último está siendo sometido, en distinto grado que aquél, a estímulos físicos relativizadores del tiempo). Por tanto, una vez admitida la naturaleza relacional del tiempo absolutamente relativo, ¿no ha perdido ya el movimiento rectilíneo uniforme su estatuto de privilegio con respecto a todos los demás "tipos" de movimiento? Es obvio que en presencia de gravedad un referencial nunca puede ser inercial, ¿pero acaso puede serlo en ausencia de gravedad?

Imaginemos un universo, sin espacio absoluto, por supuesto, en el que existen un número determinado de cuerpos, sin ninguna interacción entre ellos. No existe gravedad. Todos son cuerpos libres, sin fuerzas entre ellos. Se observan diversos tipos de movimientos (relativos, por supuesto). Puesto que cualquier cuerpo tiene derecho a considerarse en reposo, supongamos que queremos estudiar tales movimientos desde el punto de vista de uno cualquiera de ellos -el cuerpo A, por ejemplo-, ¿qué tipo de movimiento relativo observará A de cada uno de los restantes cuerpos? (Nótese que cuando intervienen rotaciones relativas las dos simetrías sobre el movimiento -según la velocidad y según la aceleración- de las que se habló en el Tractatus physico-philosophicus no se cumplen, en general, entre cuerpos que estén separados espacialmente. Es imposible, en general, conseguir que el movimiento relativo entre los referenciales libres sea rectilíneo uniforme. Este punto es clave para entender que, incluso en ausencia de gravedad, existen velocidades no locales mayores que "c").

¿Acaso un cuerpo libre no es capaz de rotar (relativamente, por supuesto)? ¿Acaso no se mantiene constante el momento angular de un cuerpo libre? Imaginemos un cuerpo B -una esfera, por ejemplo- con una rotación constante (rotación relativa a A, por supuesto) alrededor de un eje que pasa por su centro, ¿cuál será el movimiento de un punto -o de una partícula- de su superficie? ¿Acaso se trata de un movimiento rectilíneo uniforme? O a la inversa, ¿es acaso rectilíneo el movimiento de A respecto de B? ¿Existe algún cuerpo libre ¿inercial? con respecto al cual los demás cuerpos, sin excepción posible, presenten todos un movimiento rectilíneo uniforme? Con respecto a A, todos los demás cuerpos, B, C, ..., a pesar de ser cuerpos libres, ¿no presentan acaso cualquier tipo posible de movimiento, en general distinto, y esto es de hecho lo más probable, al movimiento rectilíneo uniforme? ¿No es acaso necesario un nuevo principio de inercia generalizado (en rigor, este nuevo principio más que una generalización supone una refutación del principio de inercia de Galileo-Newton)?

Puesto que la aceleración de los cuerpos libres (sí, sí, está bien dicho, �aceleración' de los cuerpos libres) depende de las derivadas de las componentes de la métrica con respecto de las tetracoordenadas y, en general, los movimientos con respecto a A de B, de C, ... son distintos entre sí ¿no es imprescindible una concepción relacional de la métrica para que de este modo la métrica para B según A pueda ser distinta de la métrica para C según A,...?

Una ecuación fundamental de la dinámica, ¿no debe poder ser aplicada, aparte de en coordenadas cartesianas, en cualquier sistema de coordenadas curvilíneas posible? ¿Cuál será la nueva ecuación fundamental de la física?

TEST LóGICO

Complete la siguiente serie histórica:

1) 2) 3) 4) ¿(...)?

En la casilla 1 aparece la segunda ley de Newton expresada tensorialmente. El supraíndice "i" puede tomar los valores 1, 2 y 3, que corresponden a las tres coordenadas cartesianas.

En la casilla 2 también aparece la segunda ley de Newton, pero ahora está "generalizada" (se ha sustituido la diferenciación ordinaria por la diferenciación covariante) para que pueda ser aplicable en cualquier sistema de coordenadas.

En la casilla 3 aparece la denominada tetrafuerza de Minkowski de la relatividad especial de Einstein. El supraíndice "" puede tomar los valores 0 (coordenada temporal), 1, 2 y 3 (coordenadas cartesianas).

¿Qué corresponde a la casilla 4? Según los relativistas corresponde esto:

, que equivale a esto: �(geodésicas)

Según los relativistas tales geodésicas son válidas, indistintamente, para describir tanto el movimiento de los graves -"geodésicas gravitatorias"- como el movimiento de los cuerpos libres con respecto a un "referencial no-inercial relativista" (el lector recordará el experimento mental del ascensor "acelerado" de Einstein según el cual los "campos ficticios no-inerciales" equivalen a campos gravitatorios reales). Teniendo en cuenta que, al igual que ocurre con un autobús "acelerado", disponemos de total libertad para "acelerar" el ascensor de Einstein como nos venga en gana y que, sin embargo, las 10 ecuaciones de campo de Einstein determinan unívocamente, sin ninguna libertad posible, las 10 componentes de la métrica (cuyas derivadas son las que se supone que son las responsables de describir dichas "aceleraciones"), ¿cómo resuelven los relativistas el ascensor de Einstein? Suponiendo una total ausencia de fuentes gravitatorias, ¿cómo generan las ecuaciones de la relatividad las métricas capaces de explicar la diversidad real de los movimientos de la naturaleza? ¿No es acaso imprescindible una concepción relacional de la métrica para que la métrica relacional �(...) según A' -�para B según A', �para C según A,...- pueda ser adaptada a los distintos movimientos, con respecto a A, de los distintos cuerpos �(...)' -B, C,...- que se quieran estudiar? La relatividad es incompatible con la absoluta relatividad del movimiento. Aunque tan sólo se atrevan a serlo localmente, se acabaron, por fin, los referenciales inerciales. El espacio absoluto de Newton no existe, luego las teorías de Einstein han muerto.

Pero según el lector ¿qué corresponde a la casilla 4?

Si los relativistas no tuviesen razón, sólo nos quedaría la siguiente alternativa lógica:

Luego sea:

la única alternativa tetradimensional posible a las geodésicas "gravitatorio-no-inerciales" relativistas lo que corresponde a la casilla 4 (otro error garrafal de la relatividad general es creer que el potencial gravitatorio viene descrito por la propia métrica. Ignora la existencia de un nuevo potencial cuyas derivadas covariantes no sean nulas).

He aquí la nueva ecuación fundamental de la Teoría Conectada (nuova scienza). ¿Al lector sí le parece bien? (Puede consultar algunas de las consecuencias que de ella se derivan en el Extracto de la Teoría Conectada.)

Por el breve momento, hasta aquí todo lo que me ha parecido oportuno enseñar.

Nota: la absoluta relatividad del movimiento exige que todas las interacciones de la naturaleza queden unificadas en un sistema único de ecuaciones. Las ecuaciones 84, 171 y 172 de la Teoría conectada han logrado hacer realidad el sueño de Einstein.

Aunque en toda obra participan, relacionalmente, tanto el uno como el otro, la inteligencia plena de una obra depende más de su receptor que de su creador. (Advertencia: se recomienda no leer la presente obra a cualquier lector que se haya sentido ofendido por la presente obra.)

Xavier Terri Castañé

39.162.085-P

Terrassa (Barcelona)

Telf. 626 64 44 80

http://xaterri.bubok.com/

Terrassa, Abril 2009